图论算法之 Dijkstra 优先队列优化

本人是初中蒟蒻，还有3天就要考CSP了，结果发现Dijkstra的优化还不会，写篇经验当作复习

Dijkstra 是计算单源最短路的算法，其时间复杂度在 \(O(n^2)\)，比 Floyd 快一个指数级。该算法其实是一种贪心的思想（蓝白点），原理比较好理解。

Dijkstra题目：

1. 【洛谷】单源最短路径（标准版）
2. 【洛谷】单源最短路径（弱化版）

首先，我们先要明确 Dijkstra 最重要的逻辑：在同一条路径上，经过的边越多，走的距离就越远

Dijkstra 的算法思想，就是一开始将起点到起点的距离标记为 \(0\)(dis[s] = 0, 其中 s 为起点)，而后进行 n 次循环，每次找出一个到起点距离 dis[u] 最短的点 u，将它从蓝点变为白点。随后枚举所有的蓝点 vi，如果以此白点为中转到达蓝点 vi 的路径 dis[u]+w[u][vi] 更短的话，就将它作为 vi 的“更短路径” dis[vi] （此时还不确定是不是vi的最短路径）。

如果这段文字你没法理解，那就请看下面几张图：

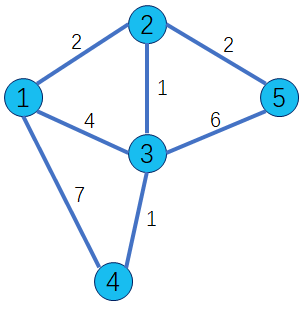
我们规定：蓝点为未被操作过的点，白点为已操作过的点。

算法开始时，作为起点的 1 号点被初始化为dis[1] = 0，其他的点dis[i]为无穷大。

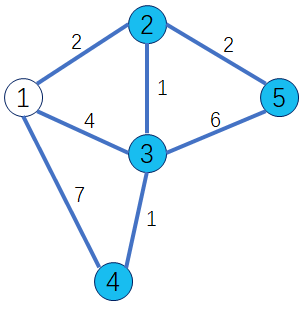
第一轮循环找到dis[1]最小，将1变成白点。

对所有的蓝点做出修改，使得 dis[2]=2,dis[3]=4,dis[4]=7。

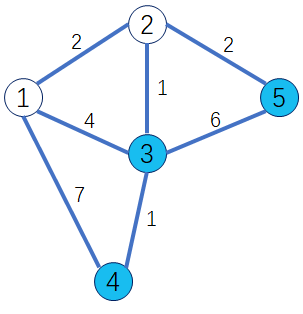
第二轮循环找到 dis[2] 最小，将 2 变为白点。与此同时，对所有的蓝点做出修改，使得 dis[3] = 3, dis[5] = 4。

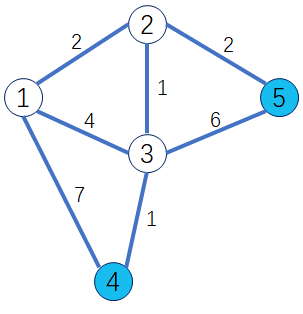
第三轮循环找到dis[3]最小，将3变成白点。对所有的蓝点做出修改，使得dis[4] = 4。发现以3为中转不能修改5，说明`3 不是5的最后一个中转点。

以此类推，从而找到最短路径。

总结下来：如果找到一个中转点i使该点与s点的路径更短，就更新dis[i]

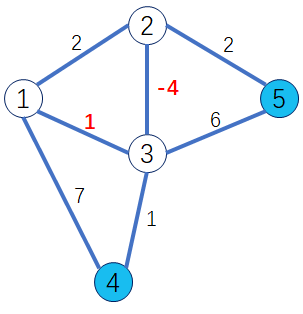
Dijkstra无法处理边权为负的情况，例如上图这个例子。
2到3的边权值为-4，显然从起点1到3的最短路径是-2（1→2→3），但是dijskstra在第二轮循环开始时会找到当前dis[i]最小的点3，并标记它为白点。
这时的dis[3]=1，然而1却不是从起点到点3的最短路径。因为3已被标记为白点，最短路径值dis[3]不会再被修改了，所以我们在边权存在负数的情况下得到了错误的答案！

（以上推导过程选自《信息学奥赛一本通》）

想明白思路，那么接下来就可以上代码了。该代码是洛谷P4479题，一道图论的模板题。

不要抄代码！！小心棕名！！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
const int N = 1e5 + 9, M = 1e6 + 9;
int n, m, s, tot;
// n: 结点个数
// m: 边数
// s: 起点
int head[N], dis[N];
bool vis[N];
struct Edge
{
    int ver, edge, next;
} g[M];
std::priority_queue < std::pair <int, int> > que;
// first: step
// second: start(current)
void add(int x, int y, int z)
{
    g[++tot] = {y, z, head[x]};
    head[x] = tot;
}
void Dijkstra()
{
    memset(dis, 0x3F, sizeof dis);
    dis[s] = 0;
    que.push(std::make_pair(0, s));
    while (!que.empty())
    {
        int x = que.top().second; que.pop();
        if (vis[x])
            continue;
        vis[x] = true;
        for (int i = head[x]; i; i = g[i].next)
        {
            int y = g[i].ver, z = g[i].edge;
            if (dis[y] > dis[x] + z)
            {
                dis[y] = dis[x] + z;
                que.push(std::make_pair(-dis[y], y));
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1, u, v, w; i <= m; i++)
        scanf("%d%d%d", &u, &v, &w), add(u, v, w);
    Dijkstra();
    for (int i = 1; i <= n; i++)
        printf("%d ", dis[i]);
    return 0;
}

有错误请指出勿喷