斐波那契数列递归的时间复杂度
f(n)=f(n-1)+f(n-2)
二阶常系数差分方程,解得:
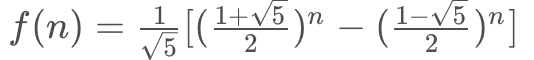
当n趋于无穷大,后面的加数趋于0,则约等于O(1.618n),即如O(2n)级别
其实可以树状展开看下,顶层是f(n),之后每层翻倍,则所有子节点的和约为2^n级别,但不会满二叉,所以比这小点。
【本文章出自博客园willaty,转载请注明作者出处,误差欢迎指出~】
f(n)=f(n-1)+f(n-2)
二阶常系数差分方程,解得:
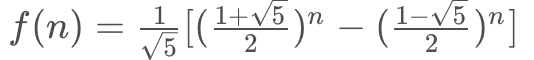
当n趋于无穷大,后面的加数趋于0,则约等于O(1.618n),即如O(2n)级别
其实可以树状展开看下,顶层是f(n),之后每层翻倍,则所有子节点的和约为2^n级别,但不会满二叉,所以比这小点。
