算法竞赛

算法竞赛2-6前缀和与差分

前缀和

• 数组a[0]~a[n-1],前缀和sum[i]等于a[0]~a[i]的和；sum[0]=a[0]    sum[1]=a[0]+a[1]   sum[2]=a[0]+a[1]+a[2].......
• 能在O(n)时间内求得所有前缀和：sum[i]=sum[i-1]+a[i]
• 预计算出前缀和，能快速计算出区间和；
  •   a[i]+a[i+1]+...+a[j-1]+a[j]=sum[j]-sum[i-1]
• 复杂度为O(n)的区间和计算，优化到了O(1)的前缀和计算。

前缀和与差分的关系

• 一维差分数组D[k]=a[k]-a[k-1],即原数组a[]的相邻元素的差

• a[k]=D[1]+D[2]+...+D[k]
• a[]是D[]的前缀和
• 差分是前缀和的逆运算：把求a[k]转化为求D的前缀和

KMP算法

算法模板

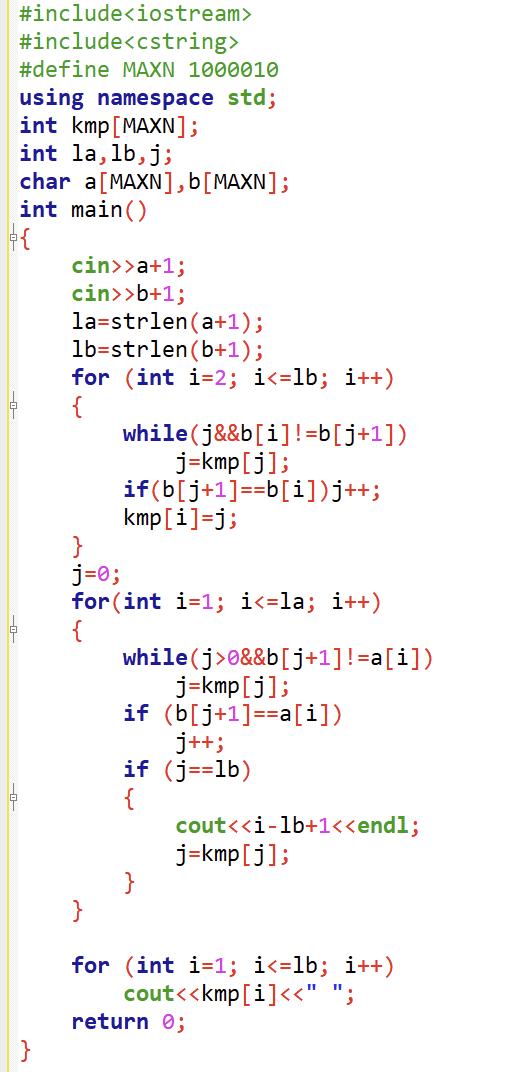时间复杂度为 $\Theta (m+n)$