分块和莫队
分块和莫队
分块
(1).基础分块
使用对象
咕
例题
咕
(2).望月悲叹最初分块
咕
(3).突刺贯穿第二分块
题意:维护一个长度为 \(n\) 的序列,进行 \(m\) 次操作。
1.将区间 \([l,r]\) 中大于 \(x\) 的数减 \(x\)。
2.查询区间 \([l,r]\) 中 \(x\) 的出现次数。
数据范围: \(1\leq n\leq 10^6,1\leq m\leq 5\times 10^5,1\leq l\leq r\leq n,0\leq a_i,x\leq 10^5+1\) 。
我们发现要维护的东西很奇怪,所以考虑分块。观察数据范围,我们发现值域比较小,所以我们考虑从值域方面下手。
设当前块内的最大值为 \(maxn\) ,当前操作要减的数为 \(x\) 。
若 \(x\geq maxn\) ,直接跳过就行。
若 \(2*x\geq maxn\) ,我们将 \(\gt x\) 的数减去 \(x\) ,这样 \(maxn\) 就会变为 \(x\)。
若 \(2*x\lt maxn\),我们将 \(\lt x\) 的数加上 \(x\),再上一个全局减 \(x\) 的标记,这样 \(maxn\) 就会变为 \(maxn-x\)。
可以发现这样 \(maxn\) 是单调不增的。
如以下代码:
点击查看代码
if(2*x>=maxn-del)
{
for(int j=maxn;j>x+del;j--)
if(siz[j]) merge(j,j-x);
maxn=min(maxn,x+del);
}
else
{
for(int j=del+1;j<=x+del;j++)
if(siz[j]) merge(j,j+x);
del+=x;
}
我们可以发现每个数最多被扫过一遍,这样时间复杂度就是 \(O(n)\) 的,因为只有 \(\sqrt n\) 个块,所以这个复杂度是可以接受的。
以上是整块的处理方式,散块的话我们将数还原回去,再暴力减就行,时间复杂度也是 \(O(n)\) 。
我们可以开一个并查集来维护,记录并修改根的值就可以,在开个数组记录每个值的出现次数,因为修改时我们不需要路径压缩,而是直接把修改前值的根接到修改后值的根上,可以直接将两个并查集 \(O(1)\) 合并,散块的话就暴力重构,复杂度 \(O(\sqrt n)\) ,这样我们就完成了第一个操作。
查询如果是整块查询,我们可以做到 \(O(1)\) 查询,如果是散块,就要查询每一个位置实际的值,复杂度为 \(O(\sqrt n)\) ,总体复杂度就是 \(O(n\sqrt n)\) 。
还没有完,我们观察范围可以发现,空间只有64MB,块都开不下。怎么解决?
观察可以发现块与块之间没有影响,我们可以离线将操作记录下来,然后一个块一个块的操作,空间就是 \(O(\sqrt n)\) ,就可以解决这个问题了。
这样,我们就完成了突刺贯穿第二分块
$\large code: $
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,kN=1e3+10,MAXN=2e5+10;
int a[N],root[MAXN],siz[MAXN],beg[kN],en[kN],pos[N],ans[N],sum[N],fa[N],val[N],n,m,len,maxn,del;
struct ask{
int op,l,r,x;
}q[N];
inline int in(){
int k=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') k=(k<<3)+(k<<1)+ch-'0',ch=getchar();
return k*f;
}
inline int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
inline void clean(){
for(int i=1;i<=maxn;i++)
siz[i]=root[i]=0;
maxn=del=0;
}
inline void build(int l,int r){
for(int i=l;i<=r;i++)
{
siz[a[i]]++;
maxn=max(maxn,a[i]);
if(root[a[i]]) fa[i]=root[a[i]];
else fa[i]=root[a[i]]=i,val[i]=a[i];
}
}
inline void merge(int x,int y){
if(root[y]) fa[root[x]]=root[y];
else root[y]=root[x],val[root[y]]=y;
siz[y]+=siz[x];
root[x]=siz[x]=0;
}
signed main(){
// freopen("1.in","r",stdin);freopen("1.out","w",stdout);
n=in(),m=in();
len=sqrt(n);
for(int i=1;i<=n;i++)
{
a[i]=in();
sum[i]=sum[i-1]+(a[i]==0);
pos[i]=(i-1)/len+1;
if(!beg[pos[i]]) beg[pos[i]]=i;
en[pos[i]]=i;
}
for(int i=1;i<=m;i++)
q[i].op=in(),q[i].l=in(),q[i].r=in(),q[i].x=in();
for(int k=1;k<=pos[n];k++)
{
int l=beg[k],r=en[k];
clean();
build(l,r);
for(int i=1;i<=m;i++)
{
int x=q[i].x,L=q[i].l,R=q[i].r;
if(R<l||L>r) continue;
if(q[i].op==1)
{
if(x>maxn-del) continue;
if(l>=L&&r<=R)
{
if(2*x>=maxn-del)
{
for(int j=maxn;j>x+del;j--)
if(siz[j]) merge(j,j-x);
maxn=min(maxn,x+del);
}
else
{
for(int j=del+1;j<=x+del;j++)
if(siz[j]) merge(j,j+x);
del+=x;
}
}
else
{
for(int j=l;j<=r;j++)
{
a[j]=val[find(j)];
root[a[j]]=siz[a[j]]=0;
a[j]-=del;
}
for(int j=l;j<=r;j++) val[j]=0;
for(int j=max(l,L);j<=min(r,R);j++)
if(a[j]>x) a[j]-=x;
maxn=del=0;
build(l,r);
}
}
else
{
if(l>=L&&r<=R)
ans[i]+=siz[x+del];
else
for(int j=max(l,L);j<=min(r,R);j++)
if(val[find(j)]==del+x) ans[i]++;
}
}
}
for(int i=1;i<=m;i++)
if(q[i].op==2)
printf("%d\n",ans[i]+(sum[q[i].r]-sum[q[i].l-1])*(q[i].x==0));
return 0;
}
莫队
(1).普通莫队
基础知识&优化
例题
P5071 [Ynoi Easy Round 2015] 此时此刻的光辉
题意:求 \(\prod\limits_{i=l}^{r} a_i\) 的约数个数, \(a_i\in[1,1e9]\)。
首先,我们可以把所有的 \(a_i\) 拆成 \(\prod\limits_{i=1}^k {p_i}^{c_i}\) 的形式,然后把它们乘起来,设第 \(k\) 个质因数的总出现个数为 \(cnt_i\) ,那么答案就是 \(\prod\limits_{i=1}^k (cnt_i+1)\) 。
因为多组询问,有的区间多次出现,还不强制在线,我们考虑莫队。那么我们怎么统计答案呢?
因为小于 \(\sqrt{1e9}\) 的质因数一共有 \(3000\) 多个,如果每次移动都要乘一遍的话我们显然会TLE,所以考虑优化。
可以发现答案可以用前缀和优化,我们可以将小于等于 \(\sqrt{1e9}\) 的用前缀和统计,剩下的跑莫队单独枚举,但小于等于 \(\sqrt{1e9}\) 的质因数还是太多了怎么办。再缩小范围,因为一个数最多有 \(2\) 个大于等于 \(\sqrt[3]{1e9}\) 的质因数,而小于等于 \(\sqrt[3]{1e9}\) 的质因数只有 \(168\) 个,我们可以对那 \(168\) 个数使用前缀和,剩下的数用莫队处理,然后统计答案的时候再乘以 \(\prod\limits_{i=1}^{168} pre_{r,i}-pre_{l-1,i}+1\),这样我们就获得了最终答案。
$\large code: $
点击查看代码
#include<bits/stdc++.h>
// #define int long long
using namespace std;
const int mod=19260817,N=1e5+10;
int a[N],inv[N<<1],n,m,pre[N][169],vis[32000],pri[3500],tot,len,ans[N],pos[N],num[N][3],pri1[32000],anss=1,cnt[2*N],tot1;
map<int,int> mp;
struct ask{
int l,r,id;
}q[N];
static inline int in(){
int k=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9')k=(k<<3)+(k<<1)+c-'0',c=getchar();
return k*f;
}
static inline bool cmp(const ask&a,const ask&b){
if(pos[a.l]!=pos[b.l]) return pos[a.l]<pos[b.l];
return pos[a.l]&1?a.r<b.r:a.r>b.r;
}
static inline void init(){
for(int i=2;i<=31622;i++)
{
if(!vis[i]) pri[++tot]=i,pri1[i]=tot;
for(int j=1;j<=tot&&pri[j]*i<=31622;j++)
{
vis[pri[j]*i]=1;
if(i%pri[j]==0) break;
}
}
inv[1]=1;
for(int i=2;i<=2*n;i++)
inv[i]=1ll*mod-1ll*inv[mod%i]*(mod/i)%mod;
}
static inline void add(int x){
for(int i=1;i<=num[x][0];i++)
{
anss=1ll*anss*inv[cnt[num[x][i]]%mod]%mod;
cnt[num[x][i]]++;
anss=1ll*anss*cnt[num[x][i]]%mod;
}
}
static inline void del(int x){
for(int i=1;i<=num[x][0];i++)
{
anss=1ll*anss*inv[cnt[num[x][i]]%mod]%mod;
cnt[num[x][i]]--;
anss=1ll*anss*cnt[num[x][i]]%mod;
}
}
static inline void work(){
int l=1,r=0;
for(int i=1;i<=m;i++)
{
while(l>q[i].l) add(--l);
while(r<q[i].r) add(++r);
while(l<q[i].l) del(l++);
while(r>q[i].r) del(r--);
int res=1;
for(int j=1;j<=168;j++)
res=1ll*res*(pre[r][j]-pre[l-1][j]+1)%mod;
ans[q[i].id]=1ll*res*anss%mod;
}
}
static inline void push(int i,int x,int num1){
if(x<=pri[168]) pre[i][pri1[x]]+=num1;
else
{
if(!mp[x]) mp[x]=++tot1;
for(int j=1;j<=num1;j++)
num[i][++num[i][0]]=mp[x];
}
}
signed main()
{
// freopen("1.in","r",stdin);freopen("1.out","w",stdout);
n=in(),m=in();
len=sqrt(n);
init();
for(int i=1;i<=n;i++)
{
pos[i]=(i-1)/len+1;
a[i]=in();
int x=a[i];
for(int j=1;j<=tot&&pri[j]*pri[j]<=x;j++)
{
if(x%pri[j]!=0) continue;
int cnt=0;
while(x%pri[j]==0)
x/=pri[j],cnt++;
push(i,pri[j],cnt);
}
if(x!=1) push(i,x,1);
for(int j=1;j<=168;j++)
(pre[i][j]+=pre[i-1][j])%=mod;
}
for(int i=1;i<=m;i++)
q[i].id=i,q[i].l=in(),q[i].r=in();
sort(q+1,q+m+1,cmp);
for(int i=1;i<=tot1;i++)
cnt[i]=1;
work();
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
///////////////////////////////////////////////////
// ♪♪♪ //
///////////////////////////////////////////////////
P5072 [Ynoi Easy Round 2015] 盼君勿忘
题意:给定一个长度为 \(n\) 的序列,\(m\) 次询问,每次询问给出 \(l,r,mod\),求每次询问区间所有子序列分别去重后的和模 \(mod\) 的值。
一个长度为 \(n\) 的序列中,假如一个数 \(x\) 出现了 \(m\) 次,那么它在所有去重后的子序列中的出现次数为 \(2^n-2^{n-m}\),贡献就是 \(x \times (2^n-2^{n-m})\)。
可以简单理解为一个序列,包含空子序列,共有 \(2^n\) 个子序列,若它出现了 \(m\) 次,则其他数共出现了 \(n-m\) 次,那么只有其他数,没有 \(x\) 的序列就有 \(2^{n-m}\) 个,贡献就是 \(x \times (2^n-2^{n-m})\)。
考虑根号分治,若这个数的出现次数 \(\leq \sqrt n\),我们将其存到一个数组里,这个数组就是用来记录出现这个次数的数的和,出现次数共有 \(\sqrt n\) 个,所以枚举的复杂度是 \(O(\sqrt n)\)。
若这个数的出现次数 \(\gt \sqrt n\),因为它们总共不超过 \(\sqrt n\) 个,所以我们可以直接在外面统计一下有哪些数出现次数可以超过 \(\sqrt n\),然后给它们存起来,然后每次询问再看它们的区间内出现次数是否大于 \(\sqrt n\),若大于统计上,否则跳过,因为会在上面的情况中统计到,这样我们的枚举次数也是 \(O(\sqrt n)\)。
数的出现次数的维护可以用莫队来解决。因为每次询问的模数不同,所以我们没法在外面存一下 \(2\) 的几次方取模后的结果,如果每次快速幂硬求,那么单次的询问就会变为 \(O(\sqrt nlog_2n)\),明显复杂度不对,但同学说能直接艹过去,所以我们使用光速幂,开两个数组,每次询问前存下模这次询问的数下 \(2^0,2^1,2^2 \dots 2^{\sqrt n}\) 和 \(2^0,2^{\sqrt n},2^{2 \times \sqrt n} \dots 2^{\sqrt n \times \sqrt n}\),这样每一个数都可以用这两个数组中的某一个数组合出来,这样就是 \(O(\sqrt n)\) 的单次询问了。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10,kN=410;
int a[N],pos[N],siz[N],st[kN],n,m,len,top,ans[N];
ll sum[N],pow1[kN],pow2[kN];
struct ask{int l,r,mod,id;}q[N];
inline bool operator<(ask a,ask b){return pos[a.l]==pos[b.l]?(pos[a.l]&1?a.r<b.r:a.r>b.r):a.l<b.l;}
inline int in(){
int k=0;
char c=getchar_unlocked();
while(c<'0'||c>'9') c=getchar_unlocked();
while(c>='0'&&c<='9') k=(k<<3)+(k<<1)+c-'0',c=getchar_unlocked();
return k;
}
inline void add(int x){
sum[siz[x]++]-=x;
sum[siz[x]]+=x;
}
inline void del(int x){
sum[siz[x]--]-=x;
sum[siz[x]]+=x;
}
inline int qmod(int x,int mod){
return pow2[pos[x]-1]*pow1[x-len*(pos[x]-1)]%mod;
}
int query(int mod,int qlen){
pow1[0]=1;
for(int i=1;i<=len;++i) pow1[i]=pow1[i-1]*2%mod;
pow2[0]=1;
for(int i=1;i<=len;++i) pow2[i]=pow2[i-1]*pow1[len]%mod;
ll res=0;
int x=qmod(qlen,mod);
int tot;
for(int i=1;i<=len;++i)
{
if(i>qlen) break;
if(!sum[i]) continue;
if(qlen==i) tot=1;
else tot=qmod(qlen-i,mod);
res=(res+1ll*sum[i]*((x-tot)%mod+mod)%mod)%mod;
}
for(int i=1;i<=top;++i)
{
int num=st[i];
if(siz[num]<=len) continue;
if(qlen==siz[num]) tot=1;
else tot=qmod(qlen-siz[num],mod);
res=(res+1ll*num*((x-tot)%mod+mod)%mod)%mod;
}
return res;
}
void work(){
int l=1,r=0;
for(int i=1;i<=m;++i)
{
while(r<q[i].r) add(a[++r]);
while(l>q[i].l) add(a[--l]);
while(r>q[i].r) del(a[r--]);
while(l<q[i].l) del(a[l++]);
ans[q[i].id]=query(q[i].mod,r-l+1);
}
return;
}
signed main(){
// freopen("1.in","r",stdin);freopen("1.out","w",stdout);
n=in(),m=in();
len=320;
for(int i=1;i<=n;++i)
a[i]=in(),pos[i]=(i-1)/len+1,siz[a[i]]++;
for(int i=1;i<=1e5;++i)
if(siz[i]>len)
st[++top]=i;
memset(siz,0,sizeof(siz));
for(int i=1;i<=m;++i)
q[i].l=in(),q[i].r=in(),q[i].mod=in(),q[i].id=i;
sort(q+1,q+m+1);
work();
for(int i=1;i<=m;++i)
printf("%d\n",ans[i]);
return 0;
}
///////////////////////////////////////////////////
// ♪♪♪ //
///////////////////////////////////////////////////
//つ ◕_◕ つ
//༼ つ ◕_◕ ༽つ
(2).回滚莫队
基础知识
例题
(3).莫队二次离线
基础知识
使用莫队时,我们可能遇到一些答案与区间内的其他数有关的问题,如求区间逆序对,假设这个操作的复杂度为 \(O(k)\) ,这时如果我们还使用普通莫队,那么复杂度就会变为 \(O(n\sqrt nk)\),时间复杂度爆炸。遇到这种情况,我们就可以使用莫队二次离线来优化,时间复杂度就会变为 \(O(nk+n\sqrt n)\)。
假设 \(f(x,[l,r])\) 为 \(x\) 对区间 \([l,r]\),的贡献。
举个例子,我们查询的区间由 \([l,r1]\) 变为了 \([l,r2]\),那么我们的答案就要加上 \(\forall x \in [l,r1],f(a_x,r1+1,r2)\)。
我们记录一个前缀和 \(suml\) 来记录到这个数为止,所有数所造成的贡献,如下图:
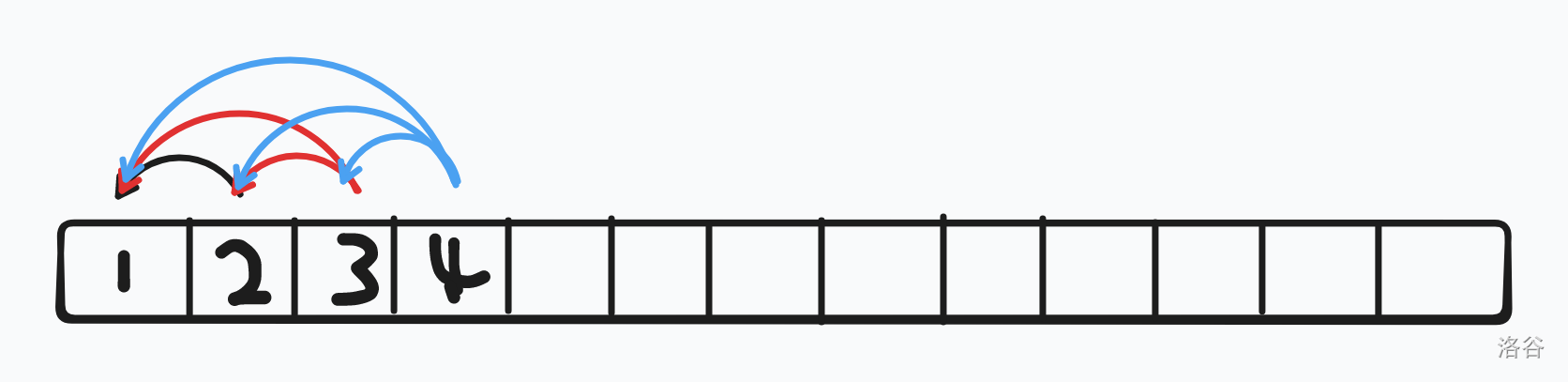
\(suml_4\) 就是真正有贡献的黑线+红线+蓝线,那么\(\forall x \in [l,r1],f(a_x,r1+1,r2)\) 就可以用 \(suml_{r2}-suml_{r1}\) 来表示吗?
显然不可以,举个例子:
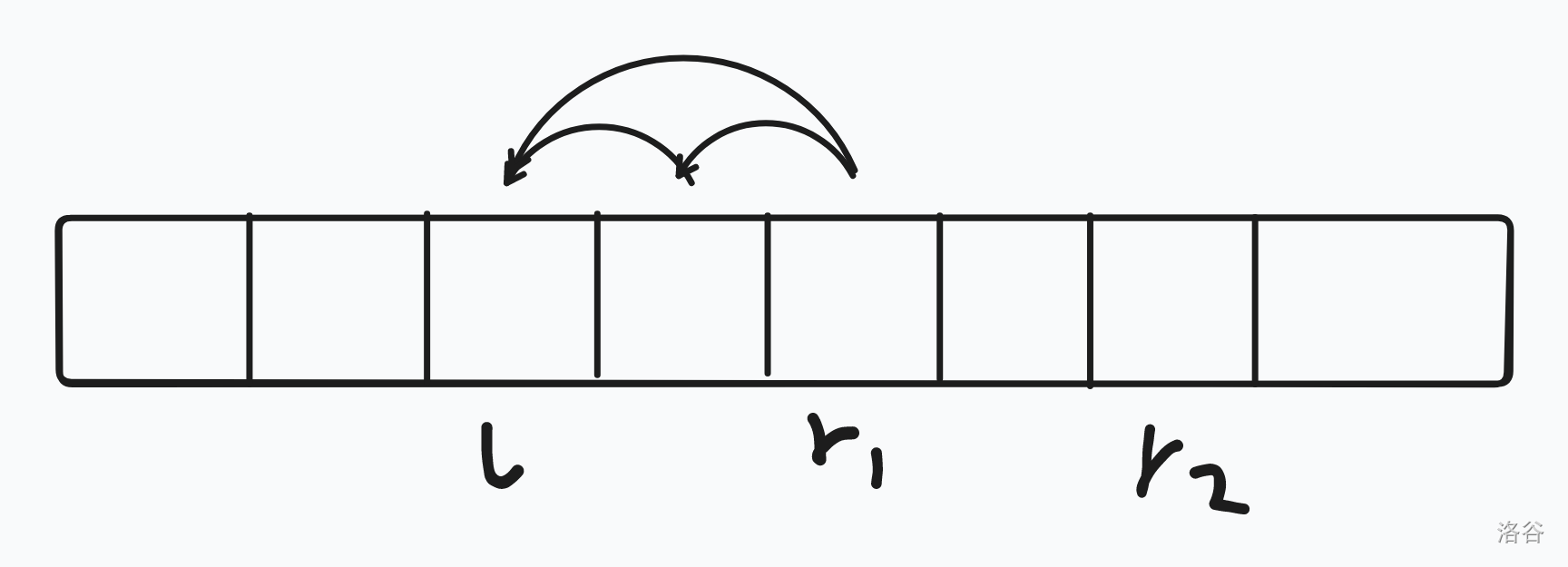
如图,这个是 \([l,r1]\) 的原本贡献。
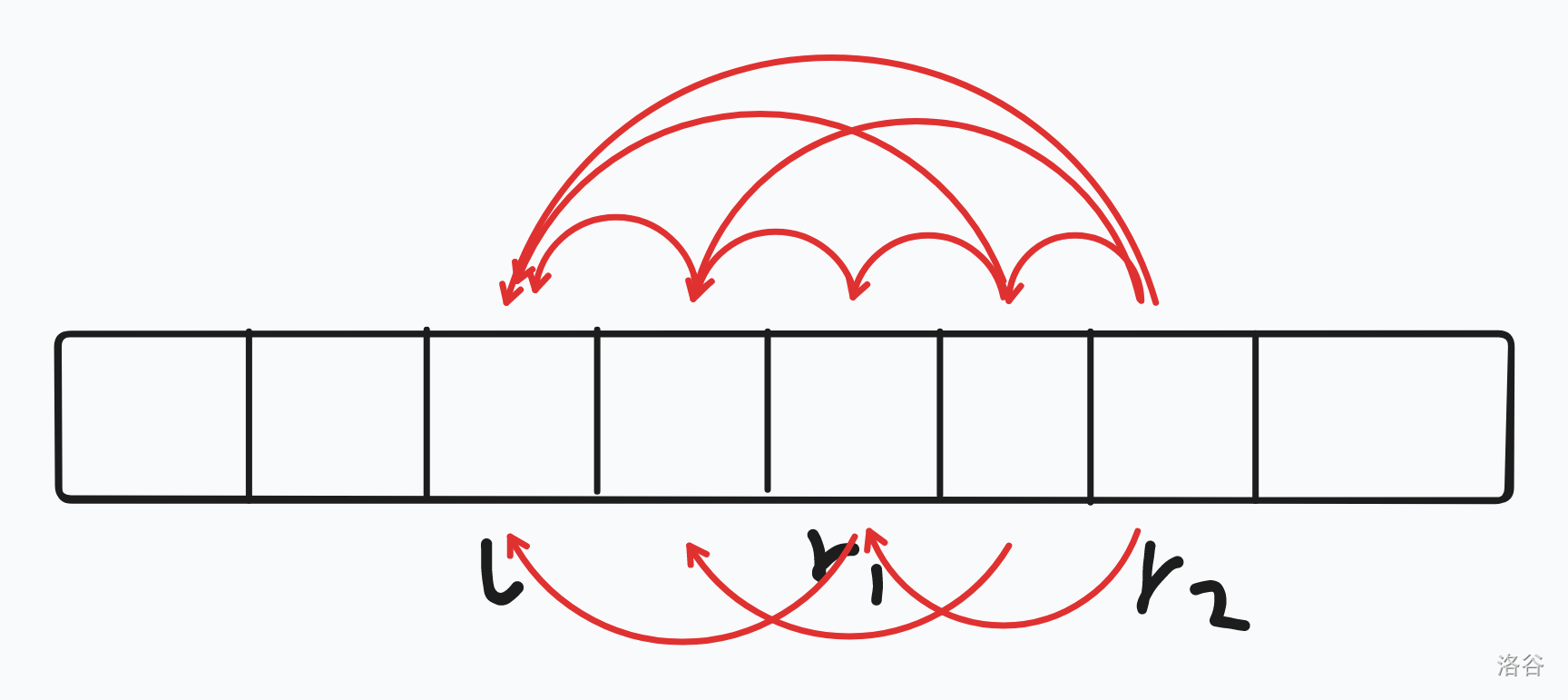
如图,这个是 \([l,r2]\) 的目标贡献。
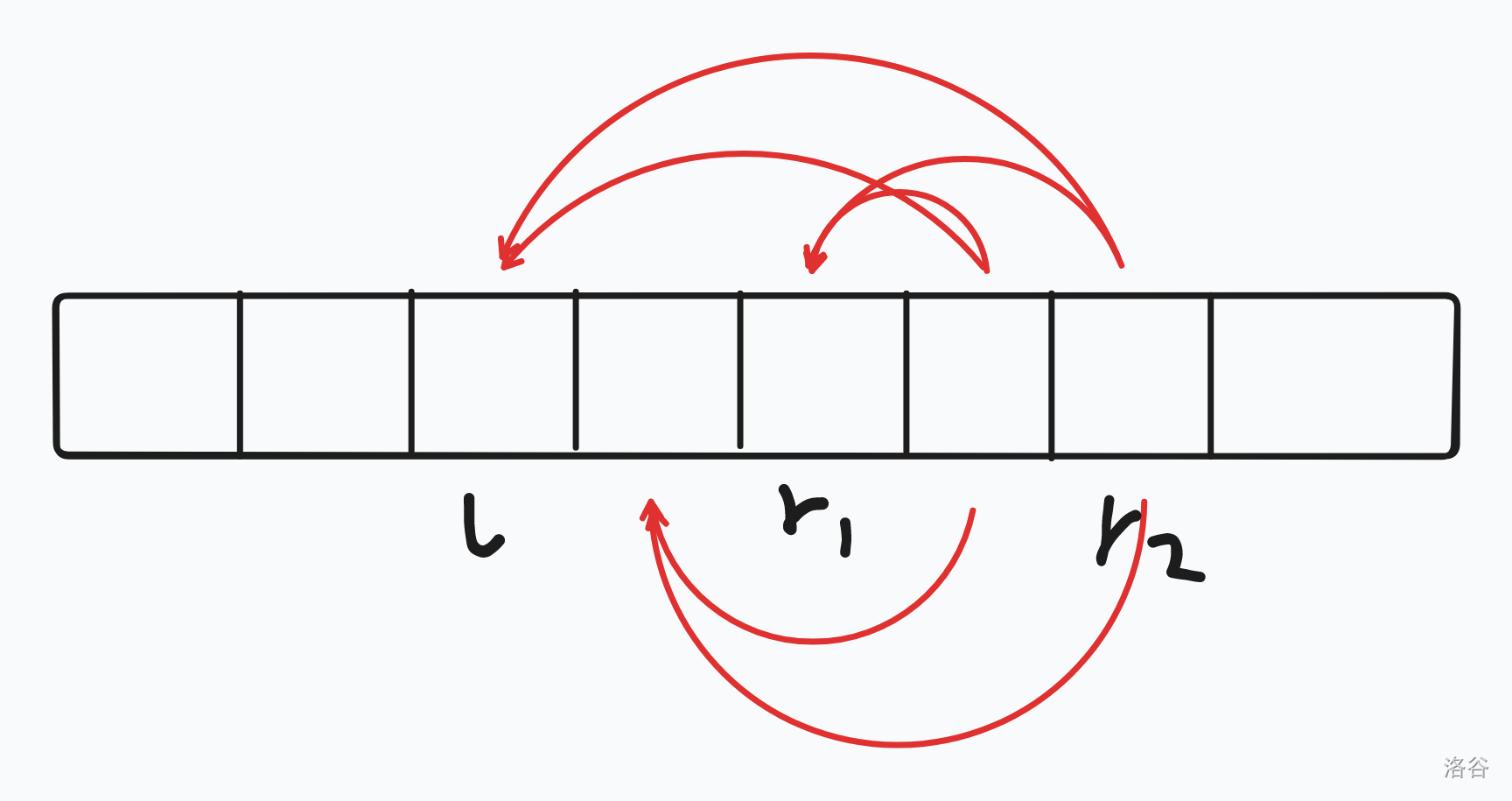
如图,这个是 \(\forall x \in [l,r1],f(a_x,r1+1,r2)\),就是我们要添加的贡献。

如图,这个是我们如果用 \(suml_{r2}-suml_{r1}\) 求出的贡献。
观察可以发现,我们多添加了下图贡献:
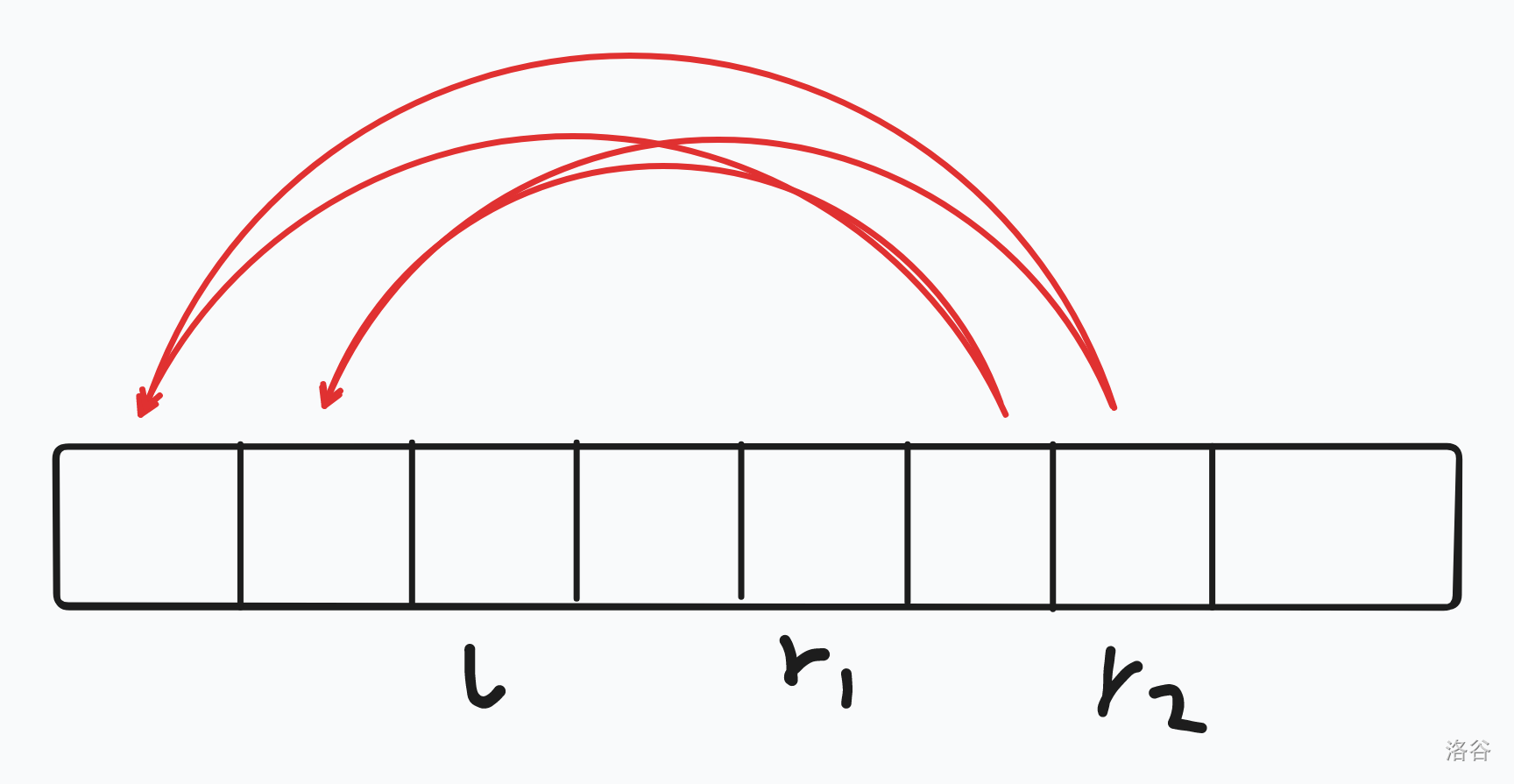
我们发现它是一个前缀多做了贡献,我们在每一个点开一个vector:\(ql\),记录到它对哪些区间多算了贡献,然后扫描线第二次离线跑一遍就可以求出正确的贡献了。
\(r\) 左移,\(l\) 左右移同理,无非再开个 \(sumr\) ,vector:\(qr\),来记录是正贡献,还是负贡献,是左边的点对右边的区间的贡献多算少算,还是右边的点对左边的区间的贡献多算少算。
二次离线是修改操作可以是 \(O(log_2n)\) 或者 \(O(\sqrt n)\),但查询一定要是 \(O(1)\),不然就成普通莫队了。
二次离线的答案要用前缀和给最终的答案加上因为你第一次离线的答案本来是以前询问上修改,以前多统计或少统计它也会一样多统计或少统计。
例题
P5047 [Ynoi2019 模拟赛] Yuno loves sqrt technology II
虽然板子是P4887,但我感觉这道更像板子
题意:给定一个长度为 \(n\) 的序列,\(m\) 次询问,每次给出 \(l,r\),求区间逆序对。
记录前缀,后缀和 \(suml,sumr\),然后用树状数组来求逆序对,时间复杂度 \(O(nlog_2n)\)。
莫队一次离线求答案,将多算,少算的贡献插入对应节点的vector中准备二次离线。然后我们扫描线左扫一遍,右扫一遍就好了,但我们要让修改的复杂度为 \(O(1)\),所以不能用树状数组了,可以搞一个分块前缀和做 \(O(\sqrt n)\) 修改,\(O(1)\) 查询。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define lb(x) x&-x
using namespace std;
constexpr int N=1e5+10,kN=330;
int a[N],n,m,b[N],siz,suml[N],sumr[N],sum[N],t[N],pos[N],len,ans[N],anss,len_siz,pos_siz[N],beg[kN],en[kN],sum_siz[N],sum_kN[kN];
struct ask{int l,r,id;}q[N];
struct node{int l,r,id,op;};
vector<node> ql[N],qr[N];
inline int in(){
int k=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') k=(k<<3)+(k<<1)+c-'0',c=getchar();
return k*f;
}
inline void add(int x,int v){
for(;x<=siz;x+=lb(x))
t[x]+=v;
}
inline int query(int x){
int res=0;
for(;x;x-=lb(x))
res+=t[x];
return res;
}
inline void add_siz(int x){
int p=pos_siz[x];
for(int i=x;i<=en[p];i++) sum_siz[i]++;
for(int i=p;i<=pos_siz[siz];i++) sum_kN[i]++;
}
inline int query_max(int x){
int p=pos_siz[x],res=0;
res=sum_siz[en[p]]-sum_siz[x];
res+=sum_kN[pos_siz[siz]]-sum_kN[p];
return res;
}
inline int query_min(int x){
int p=pos_siz[x],res=0;
if(x!=beg[p]) res=sum_siz[x-1];
res+=sum_kN[p-1];
return res;
}
bool cmp(ask a,ask b){
return pos[a.l]==pos[b.l]?(pos[a.l]&1?a.r<b.r:a.r>b.r):pos[a.l]<pos[b.l];
}
signed main(){
// freopen("1.in","r",stdin);freopen("1.out","w",stdout);
n=in(),m=in();
len=sqrt(n);
for(int i=1;i<=n;i++) b[i]=a[i]=in(),pos[i]=(i-1)/len+1;
sort(b+1,b+n+1);
siz=unique(b+1,b+n+1)-b-1;
len_siz=sqrt(siz);
for(int i=1;i<=siz;i++)
{
pos_siz[i]=(i-1)/len_siz+1;
if(!beg[pos_siz[i]]) beg[pos_siz[i]]=i;
en[pos_siz[i]]=i;
}
for(int i=1;i<=n;i++)
a[i]=lower_bound(b+1,b+siz+1,a[i])-b;
for(int i=1;i<=n;i++) suml[i]=suml[i-1]+query(siz)-query(a[i]),add(a[i],1);
memset(t,0,sizeof(t));
for(int i=n;i>=1;i--) sumr[i]=sumr[i+1]+query(a[i]-1),add(a[i],1);
for(int i=1;i<=m;i++) q[i].l=in(),q[i].r=in(),q[i].id=i;
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++)
{
if(r<q[i].r)
{
ql[l-1].push_back({r+1,q[i].r,q[i].id,-1});
anss+=suml[q[i].r]-suml[r];
r=q[i].r;
}
if(r>q[i].r)
{
ql[l-1].push_back({q[i].r+1,r,q[i].id,1});
anss-=suml[r]-suml[q[i].r];
r=q[i].r;
}
if(l<q[i].l)
{
qr[r+1].push_back({l,q[i].l-1,q[i].id,1});
anss-=sumr[l]-sumr[q[i].l];
l=q[i].l;
}
if(l>q[i].l)
{
qr[r+1].push_back({q[i].l,l-1,q[i].id,-1});
anss+=sumr[q[i].l]-sumr[l];
l=q[i].l;
}
ans[q[i].id]=anss;
}
for(int i=1;i<=n;i++)
{
add_siz(a[i]);
for(node x:ql[i])
for(int j=x.l;j<=x.r;j++)
sum[x.id]+=x.op*query_max(a[j]);
}
memset(sum_siz,0,sizeof(sum_siz));
memset(sum_kN,0,sizeof(sum_kN));
for(int i=n;i>=1;i--)
{
add_siz(a[i]);
for(node x:qr[i])
for(int j=x.l;j<=x.r;j++)
sum[x.id]+=x.op*query_min(a[j]);
}
anss=0;
for(int i=1;i<=m;i++) anss+=sum[q[i].id],ans[q[i].id]+=anss;
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
///////////////////////////////////////////////////
// ♪♪♪ //
///////////////////////////////////////////////////
//つ ◕_◕ つ
//༼ つ ◕_◕ ༽つ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号