Codeforces Round #606 (Div. 1)
Codeforces Round #606 (Div. 1)
Codeforces Round #606 (Div. 1)
A
dp:不用任何观察。只有 \(one,two\) 两种特殊的串,\(dp\) 的时候只要记录末尾是 \(o,on,t,tw\) 还是其他东西就好了
greedy:遍历字符串,遇到 \(one\) 删 \(n\)(防止产生新的 \(one\)),遇到 \(two\),如果是 \(twone\) 就删 \(o\),否则删 \(w\)
B
删掉 \(a,b\),原图分成若干连通块,把这些连通块分成三类:
1、只和 \(a\) 之间有边;2、只和 \(b\) 有边;3、和 \(a,b\) 都有
答案就是 \(1\) 类点数 \(\times\) \(2\) 类点数
#include <bits/stdc++.h>
using namespace std;
#define int long long
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 2e5 + 5, M = 1e6 + 5;
int n, m, a, b, vis[N], c, ka[N], kb[N], t[N]; vector<int> g[N];
#define pb push_back
void dfs (int u) {
vis[u] = c; ++t[c]; for (int v : g[u]) if (!vis[v]) dfs (v);
}
signed main() {
int T; read (T);
while (T--) {
read (n), read (m), read (a), read (b);
for (int i = 1; i <= n; ++i)
g[i].clear(), vis[i] = ka[i] = kb[i] = 0;
for (int i = 1, u, v; i <= m; ++i)
read (u), read (v), g[u].pb (v), g[v].pb (u);
vis[a] = vis[b] = n + 1; c = 0;
for (int i = 1; i <= n; ++i) if (!vis[i]) t[++c] = 0, dfs (i);
for (int x : g[a]) ka[vis[x]] = 1;
for (int x : g[b]) kb[vis[x]] = 1;
int sa = 0, sb = 0;
for (int i = 1; i <= c; ++i) {
if (ka[i] && !kb[i]) sa += t[i];
if (!ka[i] && kb[i]) sb += t[i];
}
printf ("%lld\n", sa * sb);
}
}
C
可以发现,如果矩形的长宽已定为 \(a\times b,a\leq b\),每种数最多能放 \(a\) 个,构造方法:把数按出现次数从大到小排序,然后斜着塞满格子,like this: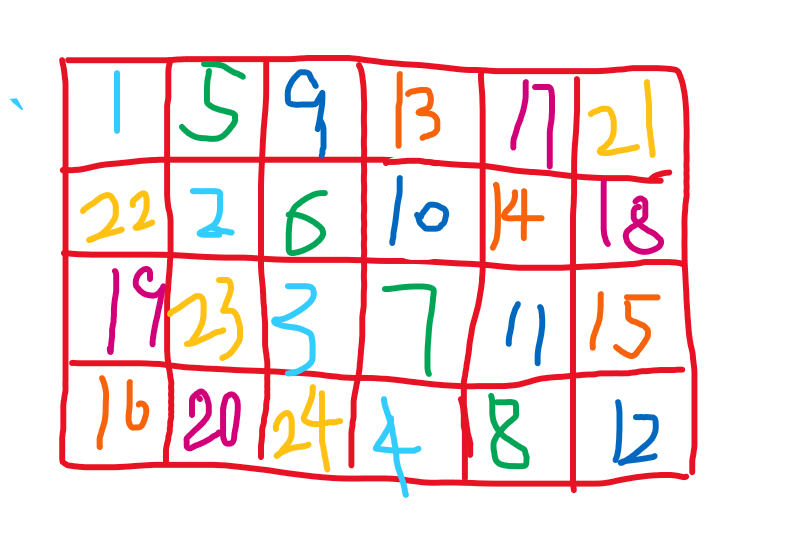
(可以自行思考为什么按次数从大到小排序后就一定不会重合)然后枚举 \(a\),判断一下 \(b\) 是否 \(\ge a\) 然后更新答案。
#include <bits/stdc++.h>
using namespace std;
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 4e5 + 5;
int n, num[N], x[N], y[N]; vector<int> z[N];
unordered_map<int, int> c; pair<int, int> p[N];
signed main() {
read (n); int s = 0, res = 0;
for (int i = 1, x; i <= n; ++i) read (x), ++num[++c[x]];
int mx = 0, a = 0, b = 0;
for (int i = 1; i <= n; ++i) {
s += num[i];
if (s / i >= i && s / i * i > mx)
a = i, b = s / i, mx = a * b;
}
printf ("%d\n%d %d\n", mx, a, b);
for (int i = 0; i < a; ++i) z[i].resize (b);
int now = 0, tx = 0, ty = 0, cc = 0, t = 0;
for (int i = 0; i < b - a + 1; ++i) {
for (int j = 0; j < a; ++j) x[++cc] = j, y[cc] = i + j;
}
for (int i = b - a + 1; i < b; ++i)
for (int j = 0; j < a; ++j) {
x[++cc] = j, y[cc] = (i + j) % b;
}
for (auto i : c) p[++t] = {i.second, i.first};
sort (p + 1, p + t + 1); reverse (p + 1, p + t + 1);
for (int i = 1; i <= t; ++i) {
int val = p[i].second, m = min (p[i].first, a);
if (now + m > mx) m = mx - now;
for (int j = 1; j <= m; ++j)
++now, z[x[now]][y[now]] = val;
if (now == mx) break;
}
for (int i = 0; i < a; ++i) {
for (int j : z[i]) printf ("%d ", j); puts ("");
}
return 0;
}
D
这里写一个比较详细的。简洁的可以看这里
因为删除的时候边有先后顺序,这题 \(dp\) 的状态和转移基于时间
状态设置( \(x\) 是什么时候被删除的?或者没被删除?):\(f_{x,0/1/2/3}\) 分别表示:点 \(x\) 被父亲边之前的边删除、点 \(x\) 被父亲边删除、点 \(x\) 被父亲边之后的边删除、点 \(x\) 没有被删除 四种情况下 \(x\) 子树内的答案。
转移:
对于 \(f_{x,0/2}\),\(x\) 不是被父亲边删除,那一定是被和儿子相连的边删除。枚举这个儿子 \(y\)。\(y\) 此时还没被删,取 \(f_{y,2/3}\)。对于其他儿子 \(z\),按照时间分类:
1、\((x,z)\) 在 \((x,y)\) 前,记为 \(z<y\)。如果这时候 \(z\) 还在,说明 \(x\) 已经没了,不符合情况。所以取 \(f_{z,0/1}\)
2、\((x,z)\) 在 \((x,y)\) 后,记为 \(z > y\) 。后面的时间点对当前不影响,但不能被父亲边删,因为 \(x\) 已经挂了,取 \(f_{z,0/2/3}\)
有 \(f_{x,0/2}=\sum\limits_{y\in son(x),y<fa_x(y>fa_x)}(f_{y,2/3}\times\prod\limits_{z<y}f_{z,0/1}\times \prod\limits_{z>y}f_{z,0/2/3})\)
注:上式中对于 \(f_{x,0}\) 和 \(f_{x,2}\) 所选的 \(y\) 条件不同,即在父亲边之前和父亲边之后
对于 \(f_{x,1}\):
1、所有 \(y<fa_x\) 已经不在(如果在,\(x\) 就挂了),并且 \((x,y)\) 这条边不可能删除 \(x\),所以 \(y\) 的删除不会拖到 \((x,y)\) 之后,不能取 \(f_{y,2}\),只能取 \(f_{y,0/1}\)。
2、\(y>fa_x\),还是随便 \(y\) 怎么样,但因为 \((x,y)\) 这条边还没弄,所以不能取 \(f_{y,1}\),剩下的 \(f_{y,0/2/3}\) 均可
**得 \(f_{x,1}=\prod\limits_{y<fa_x}f_{y,0/1}\times\prod\limits_{y>fa_x}f_{y,0/2/3}\) **
对于 \(f_{x,3}\),所有儿子 \(y\) 肯定都挂了,并且不会拖到 \((x,y)\) 以后。取 \(f_{y,0/1}\)
即 \(f_{x,3}=\prod\limits_{y\in son(x)}f_{y,0/1}\)
代码里直接把多重式拆出来算了,可能有些怪
#include <bits/stdc++.h>
using namespace std;
#define int long long
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 2e5 + 5, mod = 998244353;
int n, f[N][4]; vector<int> g[N];
#define pb push_back
void dfs (int u, int la) {
int sum = 0, s = 1, sa = 1, sb = 1, k = 0; f[u][3] = f[u][1] = 1;
for (int v : g[u]) if (v != la) {
dfs (v, u);
(f[u][2] *= (f[v][0] + f[v][2] + f[v][3])) %= mod;
(f[u][0] *= (f[v][0] + f[v][2] + f[v][3])) %= mod;
if (!k) {
(f[u][0] += s * (f[v][2] + f[v][3])) %= mod;
(f[u][1] *= (f[v][0] + f[v][1])) %= mod;
} else {
(f[u][2] += s * (f[v][2] + f[v][3])) %= mod;
(f[u][1] *= (f[v][0] + f[v][2] + f[v][3])) %= mod;
}
(s *= (f[v][0] + f[v][1])) %= mod;
(f[u][3] *= (f[v][0] + f[v][1])) %= mod;
} else k = 1;
}
signed main() {
read (n);
for (int i = 1, u, v; i < n; ++i)
read (u), read (v), g[u].pb (v), g[v].pb (u);
dfs (1, 0);
printf ("%lld\n", (f[1][0] + f[1][3]) % mod);
}
E
先特判掉所有数相同的情况
设 \(a_i=k_ig+d\),\(g,d\) 为定值,即所有 \(a_i\) 对 \(g\) 同余,那么所有可以到达的位置 \(w\) 都可以表示为 \(kg+d\),这样就可以把 \(g\) 当作一个单位长度。容易发现 \(g|(a_1-a_0),g|(a_2-a_0),g|(a_3-a_0)\),因为 \(g\) 作为一个单位长度,那么感性理解 \(g\) 越大问题越简化,取最大值 \(gcd((a_1-a_0),(a_2-a_0),(a_3-a_0))\),事实上,因为 \(g\) 的最大化,所有 \(k_i\) 互素,才能进行判断无解和构造答案。
先讲讲有解的条件:
1、对于所有 \(b_i\) 满足 \(b_i\%g=d\)
2、\(a_i=k_ig+d,b_i=p_ig+d\),则 \(k_i,p_i\) 的奇偶性可以一一配对。因为操作不会改变系数的奇偶。
满足以上条件后,如何构造出一组解呢?
以 \(k_i,p_i\) 为新坐标重新观察这个问题。
step1:先将 \(k,p\) 分别移动到 \([x,x+1],[y,y+1]\)
设 \(d\) 为两个石子间的最远距离,目标就是让 \(d\leq1\)。假设 \(k_0\leq k_1\leq k_2\leq k_3\),以下做法每次能让 \(d\) 至少减少 \(\frac{1}{4}\)。
1、如果有某个 \(k_i\in [k_0+\frac{d}{4},k_0+\frac{3d}{4}]\),\(i=1\) 则操作 \((0,1)\),\(i=2\) 操作 \((3,2)\)。容易发现这样操作后 \(d'\leq\frac{3d}{4}\)
2、不存在这样的 \(i\),...
写不下去了,感觉这题意义不是很大(🤣就放这里了
F
刚在学 \(SAM\) 的时候ccf出考纲了,这好像只有 \(CTS\) 才会出,而且我太懒了,就算了。某时某地突然兴起可能会去学学
连跳两题...啊这
upd:来补题了
除了 \(s*t\) 形式的答案都可以简单计算。那么我们来看 \(s*t\)
对于 \(end\) \(points\) 集合相同的 \(s\) 可选的 \(t\) 相同,那么枚举 \(end\ points\) 种类。对于一个固定的 \(t\) 的集合,方案数就是把所有串插入 \(Trie\) 后的节点数量。 计算 \(Trie\) 节点数量的一个简单方法:把字符串排序,节点数量 \(num=\sum |t_i| -\sum |lcp(t_i,t_{i-1})|\),后半段可以通过 \(SA\) 快速计算
在 \(SAM\) 的 \(parent\) 上,父节点的 \(end\ points\) 是所有子节点的并,由此可以考虑启发式合并,合并 \(set\) 的的时候一边 \(insert\) 一边 \(update\) 答案
复杂度 \(O(n\ log^2n)\)
#include <bits/stdc++.h>
using namespace std;
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 1e5 + 5, M = N << 1;
int n, tot = 1, lst = 1, ch[M][26], link[M], len[M]; char a[N];
void extend (int c) {
int p = lst, np = lst = ++tot;
len[np] = len[p] + 1;
for (; p && !ch[p][c]; p = link[p]) ch[p][c] = np;
if (!p) { link[np] = 1; return; }
int q = ch[p][c];
if (len[q] == len[p] + 1) { link[np] = q; return; }
int nq = ++tot;
memcpy (ch[nq], ch[q], 26 << 2), link[nq] = link[q];
len[nq] = len[p] + 1, link[np] = link[q] = nq;
for (; p && ch[p][c] == q; p = link[p]) ch[p][c] = nq;
}
vector<int> g[M];
#define pb push_back
int m = 1e5, sa[N], rk[N], c[N], id[N], t[N], h[N], rrk[N];
bool cmp(int x, int y, int w) {
return rrk[x] == rrk[y] && rrk[x + w] == rrk[y + w];
}
void getsa () {
for (int i = 1; i <= n; ++i) ++c[rk[i] = a[i]];
for (int i = 1; i <= m; ++i) c[i] += c[i - 1];
for (int i = n; i >= 1; --i) sa[c[rk[i]]--] = i;
int p = 0;
for (int w = 1; w < n; w <<= 1, m = p, p = 0) {
for (int i = n; i > n - w; --i) id[++p] = i;
for (int i = 1; i <= n; ++i) if (sa[i] > w) id[++p] = sa[i] - w;
memset (c, 0, sizeof (c));
for (int i = 1; i <= n; ++i) ++c[t[i] = rk[id[i]]];
for (int i = 1; i <= m; ++i) c[i] += c[i - 1];
for (int i = n; i >= 1; --i) sa[c[t[i]]--] = id[i];
memcpy (rrk, rk, sizeof (rk)); p = 0;
for (int i = 1; i <= n; ++i)
rk[sa[i]] = cmp (sa[i], sa[i - 1], w) ? p : ++p;
}
for (int i = 1, j = 0; i <= n; ++i) {
if (j) --j;
while (a[i + j] == a[sa[rk[i] - 1] + j]) ++j;
h[rk[i]] = j;
}
}
int st[N][20], lg[N];
void getst () {
for (int i = 1; i <= n; ++i) st[i][0] = h[i];
for (int j = 1; j <= 17; ++j)
for (int i = 1; i + (1 << j) - 1 <= n; ++i)
st[i][j] = min (st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;
}
int ask (int l, int r) {
int t = lg[r - l + 1];
return min (st[l][t], st[r - (1 << t) + 1][t]);
}
struct yxl {
set<int> s; long long val;
void init () { s.insert (0), s.insert (n + 1); }
void ins (int x) {
if (s.count (x)) return;
int l = *(--s.lower_bound (x));
int r = *s.upper_bound (x);
val += n - sa[x] + 1;
if (l >= 1) val -= ask (l + 1, x);
if (r <= n) val -= ask (x + 1, r);
if (l >= 1 && r <= n) val += ask (l + 1, r);
s.insert (x);
}
} s[M];
long long res;
void dfs (int u) {
for (int v : g[u]) {
dfs (v);
if (s[v].s.size() > s[u].s.size())
swap (s[u], s[v]);
for (int x : s[v].s) s[u].ins (x);
}
res += s[u].val * (len[u] - len[link[u]]);
}
signed main() {
scanf ("%s", a + 1); n = strlen (a + 1);
for (int i = 1; i <= n; ++i) extend (a[i] - 'a');
getsa (); getst ();
///////
for (int i = 1; i <= tot; ++i) res += len[i] - len[link[i]];
///////
int now = 1;
for (int i = 1; i <= n; ++i) now = ch[now][a[i] - 'a'];
for (int i = 1; i <= tot; ++i)
if (i != now) res += len[i] - len[link[i]];
///////
for (int i = 1; i <= tot; ++i) g[link[i]].pb (i), s[i].init ();
now = 1; s[now].ins (rk[2]);
for (int i = 1; i <= n - 2; ++i) {
s[now = ch[now][a[i] - 'a']].ins (rk[i + 2]);
}
dfs (1);
///////
res += s[1].val;
///////
printf ("%lld\n", res + 2);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号