决策树2-构造决策树的算法 ID3、C4.5

1.决策树的本质

if-then规则：决策树可以看做一个if-then规则的集合。我们从决策树的根结点到每一个叶结点的路径构建一条规则。

 并且我们将要预测的实例都可以被一条路径或者一条规则所覆盖，且只被一条路径或者一条规则所覆盖（互斥完备）。

2.构造决策树算法

决策树学习的关键其实就是选择最优划分属性，希望划分后，分支结点的“纯度”越来越高。

那么“纯度”的度量方法不同，也就导致了学习算法的不同，这里我们讲解最常见的俩种算法，ID3算法与C4.5算法。

2.1ID3算法

2.1.1算法思想

我们既然希望划分之后结点的“纯度”越来越高，那么如何度量纯度呢？

“信息熵”是度量样本集合不确定度（纯度）的最常用的指标。

在我们的ID3算法中，我们采取信息增益这个量来作为纯度的度量。

我们选取使得信息增益最大的特征进行分裂！那么信息增益又是什么概念呢？

我们前面说了，信息熵是代表随机变量的复杂度（不确定度）通俗理解信息熵，条件熵代表在某一个条件下，随机变量的复杂度（不确定度）通俗理解条件熵。

而我们这里说的的信息增益恰好是：信息熵-条件熵。

 

我们用下面这个公式计算一个系统的熵：

 

 

 

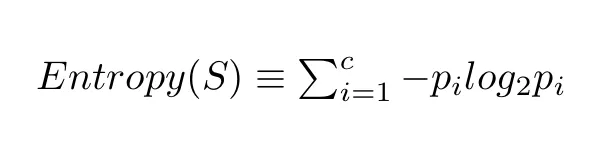
 在这个公式中，c 代表类别或属性的总数，p_i 代表属于第 i 类的样本所占的比例。

举个例子来说，我们有两个类别：红色（R）和蓝色（B）。第一个袋子里有 25 块红色巧克力。巧克力总数是 50。因此，p_i=25/50。蓝色类别也是这样处理。把这些值代入熵方程，我们得到以下结果：

 

 

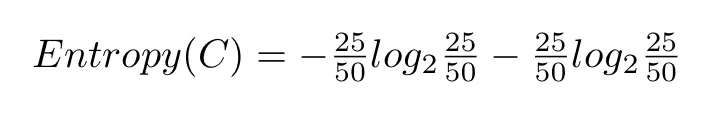
 信息增益的定义为：

 

 

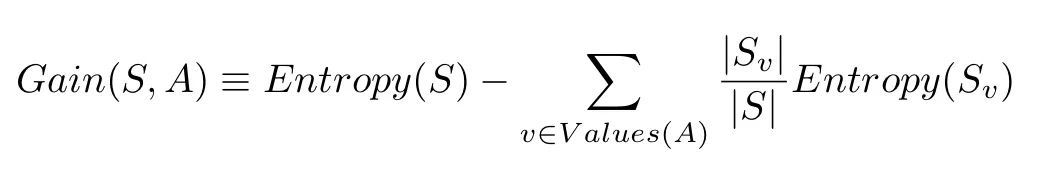
 S 代表整个样本集，A 代表我们想要分割的属性。|S| 代表样本数量，|Sv| 表示当前属性 A 值的样本数量。

 

信息增益表示得知属性 a 的信息而使得样本集合不确定度减少的程度

那么我们现在也很好理解了，在决策树算法中，我们的关键就是每次选择一个特征，特征有多个，那么到底按照什么标准来选择哪一个特征。

对于ID3算法来说，这个问题就可以用信息增益来度量。

如果选择一个特征后，信息增益最大（信息不确定性减少的程度最大），那么我们就选取这个特征。

好的，我们现在已经知道了选择指标了，就是在所有的特征中，选择信息增益最大的特征。那么如何计算呢？看下面例子：

 

 

 

 

 

 

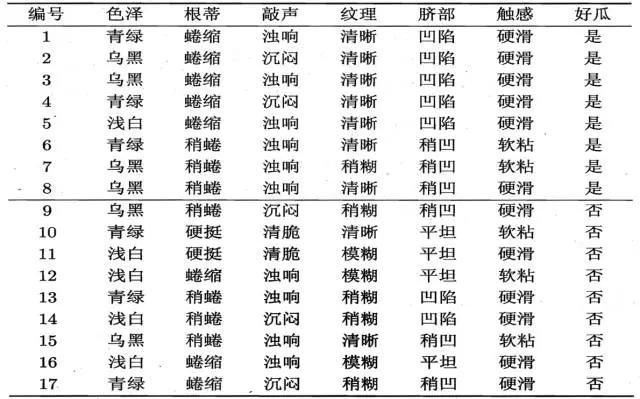
正例(好瓜)占 8/17，反例占 9/17 ，根结点的信息熵为

 

 

 

 

 

计算当前属性集合{色泽，根蒂，敲声，纹理，脐部，触感}中每个属性的信息增益

色泽有3个可能的取值：{青绿，乌黑，浅白}

D1(色泽=青绿) = {1, 4, 6, 10, 13, 17}，正例  3/6，反例 3/6

D2(色泽=乌黑) = {2, 3, 7, 8, 9, 15}，正例  4/6，反例 2/6

D3(色泽=浅白) = {5, 11, 12, 14, 16}，正例  1/5，反例 4/5

3 个分支结点的信息熵

 

 

 

 

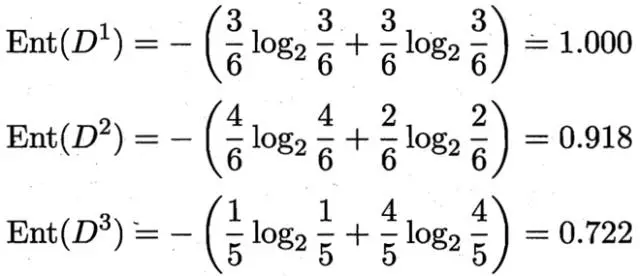
那么我们可以知道属性色泽的信息增益是：

 

 

 

 

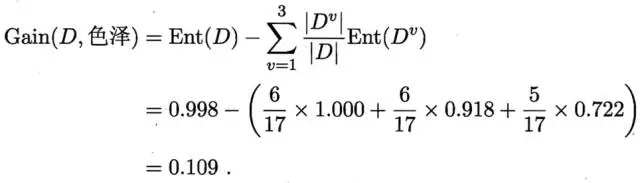
同理，我们可以求出其它属性的信息增益，分别如下：

 

 

 

 

于是我们找到了信息增益最大的属性纹理，它的Gain(D，纹理) = 0.381最大。

所以我们选择的划分属性为“纹理”

如下：

 

 

 

 

 

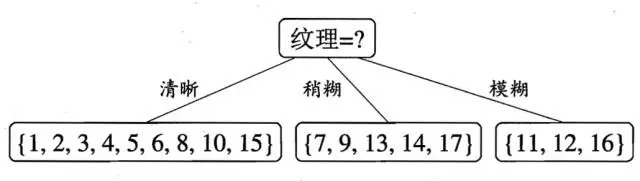
根据纹理属性划分后，我们可以得到了三个子结点。

对于这三个子节点，我们可以递归的使用刚刚找信息增益最大的方法进行选择特征属性，

比如：D1(纹理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15}，第一个分支结点可用属性集合{色泽、根蒂、敲声、脐部、触感}，基于 D1各属性的信息增益，分别求的如下：

 

 

 

 

 

于是我们可以选择特征属性为根蒂，脐部，触感三个特征属性中任选一个（因为他们三个相等并最大）。

其它俩个子结点同理，然后得到新一层的结点，再递归的由信息增益进行构建树即可
我们最终的决策树如下：

 

 

 

 

 

 

 

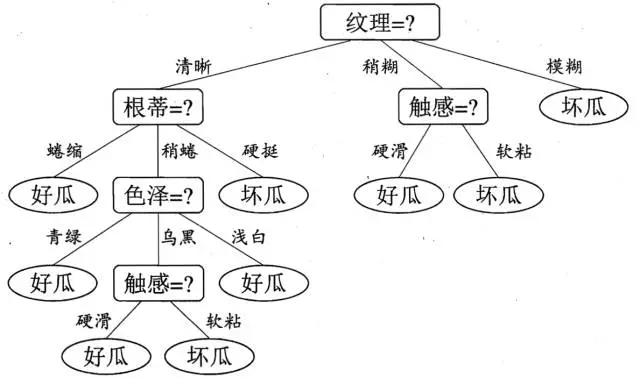
2.1.2算法实现

有了上述概念，我们就可以开始开始决策树的训练了，训练过程分为：
　　１. 选取特征，分割样本集
　　２. 计算增益，如果增益够大，将分割后的样本集作为决策树的子节点，否则停止分割
　　３. 递归执行上两步

 

算法框架如下

class DecisionTree(object):
    def fit(self, X, y):
        # 依据输入样本生成决策树
        self.root = self._build_tree(X, y)

    def _build_tree(self, X, y, current_depth=0):
        #1. 选取最佳分割特征，生成左右节点
        #2. 针对左右节点递归生成子树
      
    def predict_value(self, x, tree=None):
        # 将输入样本传入决策树中，自顶向下进行判定
        # 到达叶子节点即为预测值

在上述代码中，实现决策树的关键是递归构造子树的过程，为了实现这个过程，我们需要做好三件事：分别是节点的定义，最佳分割特征的选择，递归生成子树。

 

2.13ID3算法与C4.5算法的关系

不同的决策树学习算法只是它们选择特征的依据不同，决策树的生成过程都是一样的（根据当前环境对特征进行贪婪的选择）。

 

我们从上面求解信息增益的公式中，其实可以看出，ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征，每一次都选择使得信息增益最大的特征进行分裂，递归地构建决策树。ID3算法以信息增益作为划分训练数据集的特征，有一个致命的缺点。选择取值比较多的特征往往会具有较大的信息增益，所以ID3偏向于选择取值较多的特征。

现在假如我们把数据集中的“编号”也作为一个候选划分属性。我们可以算出“编号”的信息增益是0.998

因为每一个样本的编号都是不同的（由于编号独特唯一，条件熵为0了（可以通过前面的例子，计算），每一个结点中只有一类，纯度非常高啊）。

也就是说，来了一个预测样本，你只要告诉我编号，其它特征就没有用了，这样生成的决策树显然不具有泛化能力。

于是我们就引入了信息增益率来选择最优划分属性！

而信息增益率也是C4.5算法的核心思想。

 

这次我们每次进行选取特征属性的时候，不再使用ID3算法的信息增益，而是使用了信息增益率这个概念。

 

首先我们来看信息增益率的公式：

 

 

 

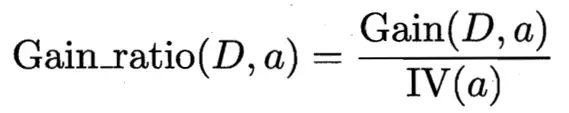
由上图我们可以看出，信息增益率=信息增益/IV(a),说明信息增益率是信息增益除了一个属性a的固有值得来的。

 

我们一开始分析到，信息增益准则其实是对可取值数目较多的属性有所偏好！（比如上面提到的编号，如果选取编号属性，每一个子节点只有一个实例，可取值数目是最多，而且子节点纯度最高《只有一个类别》，导致信息增益最大，所以我们会倾向于选他，但是已经分析了这种树是不具备泛化能力的）。

 

但是刚刚我们分析到了，信息增益并不是一个很好的特征选择度量。于是我们引出了信息增益率。

 

我们来看IV(a)的公式：

属性a的固有值：

 

 

 

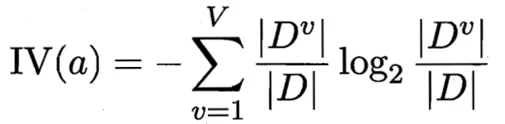
IV(触感) = 0.874 ( V = 2 )

IV(色泽) = 1.580 ( V = 3 )

IV(编号) = 4.088 ( V = 17 )

 

由上面的计算例子，可以看出IV(a)其实能够反映出，当选取该属性，分成的V类别数越大，IV(a)就越大，如果仅仅只用信息增益来选择属性的话，那么我们偏向于选择分成子节点类别大的那个特征。

 

但是在前面分析了，并不是很好，所以我们需要除以一个属性的固定值，这个值要求随着分成的类别数越大而越大。于是让它做了分母。

 

这样可以避免信息增益的缺点。

因为一开始我仅仅用信息增益作为我的选择目标，但是会出现“编号”这些使得类别数目多的属性选择，但是又不具有泛化能力，所以我给他除以一个值（这个值）随着你分的类别越多，我就越大，一定程度上缓解了信息增益的缺点

 

那么信息增益率就是完美无瑕的吗？

 

当然不是，有了这个分母之后，我们可以看到增益率准则其实对可取类别数目较少的特征有所偏好！

 

毕竟分母越小，整体越大。

 

所以C4.5算法不直接选择增益率最大的候选划分属性，候选划分属性中找出信息增益高于平均水平的属性（这样保证了大部分好的的特征），再从中选择增益率最高的（又保证了不会出现编号特征这种极端的情况）