机器学习--Logistic回归
 总览:
总览:
1.摘要
2.问题引入
3.逻辑回归问题的几何描述
3.1通俗描述
3.2解析几何的知识找到逻辑回归问题的分界线
3.3从概率角度看待Z
4.构造代价函数求出参数的值
4.1构造代价函数(从极大似然函数引入)
4.2使用梯度下降法求解参数
5.从特征处理的角度重新梳理我们刚才的分析过程
1.摘要
线性回归能对连续值结果进行预测,而逻辑回归则是应用非常广泛的一个分类机器学习算法,它将数据拟合到一个logit函数(或者叫做logistic函数)中,从而能够完成对事件发生的概率进行预测。比如说医生需要判断病人是否生病,银行要判断一个人的信用程度是否达到可以给他发信用卡的程度,邮件收件箱要自动对邮件分类为正常邮件和垃圾邮件等等。
2.问题引入
为研究与急性心肌梗塞急诊治疗情况有关的因素,现收集了200个急性心肌梗塞的病例,如下表所示。其中,X1 用于指示救治前是否休克,X1=1 表示救治前已休克,X1=0 表示救治前未休克;X2 用于指示救治前是否心衰,X2=1 表示救治前已发生心衰,X2=0 表示救治前未发生心衰;X3用于指示12小时内有无治疗措施,X3=1表示没有,否则X3=0。最后给出了病患的最终结局,当 P=0 时,表示患者生存;否则当 P=1 时,表示患者死亡。
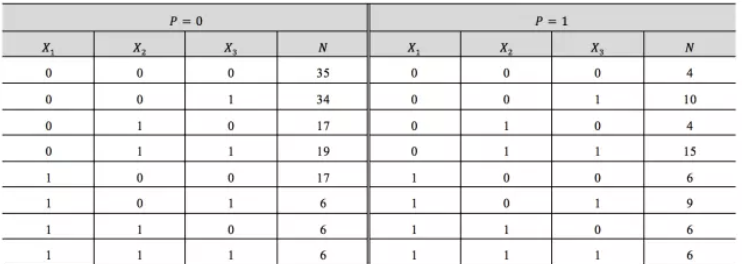
如果要建立回归模型,进而来预测不同情况下病患生存的概率,考虑用多重回归来做,(注意我们将大写换成了小写)即
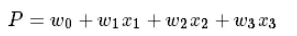
则显然将自变量带入上述回归方程,不能保证概率 P 一定位于0~1。于是想到用Logistic函数将自变量映射至0~1。Logistic函数的定义如下: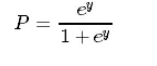
或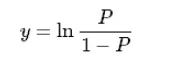
然后上面的函数定义式将多元线性回归中的因变量替换得到
其中 x=w0+w1x1+⋯+wnxn,而且在我们当前所讨论的例子中 n=3。
上式中的 w0,w1,⋯,wn正是我们要求的参数,通常采用极大似然估计法对参数进行求解。对于本题而言则有
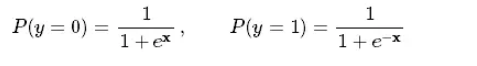
3.逻辑回归问题的几何描述
3.1通俗描述
逻辑回归处理的是分类问题。我们可以用通俗的几何语言重新表述它:
空间中有两群点,一群是圆点“〇”,一群是叉点“X”。我们希望从空间中选出一个分离边界,将这两群点分开。


为了简化处理和方便表述,我们做以下4个约定:
我们先考虑在二维平面下的情况。
而且,我们假设这两类是线性可分的:即可以找到一条最佳的直线,将两类点分开。
用离散变量y表示点的类别,y只有两个可能的取值。y=1表示是叉点“X”,y=0表示是是圆点“〇”。
点的横纵坐标用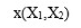 表示。
表示。
于是,现在的问题就变成了:怎么依靠现有这些点的坐标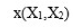
和标签(y),找出分界线的方程。
3.2解析几何的知识找到逻辑回归问题的分界线
我们用逆推法的思路:
1.假设我们已经找到了这一条线,再寻找这条线的性质是什么。根据这些性质,再来反推这条线的方程。
2.这条线有什么性质呢?
首先,它能把两类点分开来。——好吧,这是废话。( ̄▽ ̄)”
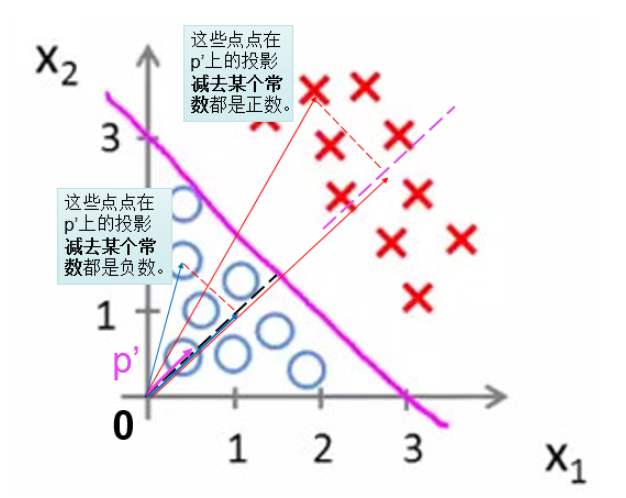
然后,两类点在这条线的法向量p上的投影的值的正负号不一样,一类点的投影全是正数,另一类点的投影值全是负数!
首先,这个性质是非常好,可以用来区分点的不同的类别。
而且,我们对法向量进行规范:只考虑延长线通过原点的那个法向量p。这样的话,只要求出法向量p,就可以唯一确认这条分界线,这个分类问题就解决了。

3.还有什么方法能将法向量p的性质处理地更好呢?
因为计算各个点到法向量p投影,需要先知道p的起点的位置,而起点的位置确定起来很麻烦,我们就干脆将法向量平移使其起点落在坐标系的原点,成为新向量p’。因此,所有点到p’的投影也就变化了一个常量。
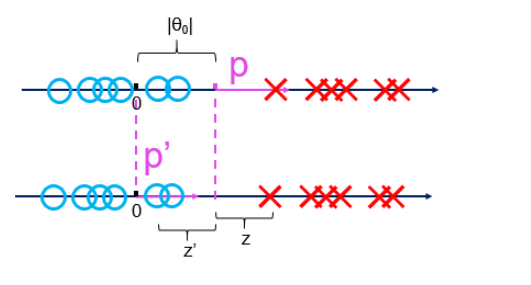

3.3从概率角度看待Z
我们由点x的坐标得到了一个新的特征z,那么:
z的现实意义是什么呢?
首先,我们知道,z可正可负可为零。而且,z的变化范围可以一直到正负无穷大。
z如果大于0,则点x属于y=1的类别。而且z的值越大,说明它距离分界线的距离越大,更可能属于y=1类。
那可否把z理解成点x属于y=1类的概率P(y=1|x) (下文简写成P)呢?显然不够理想,因为概率的范围是0到1的。
但是我们可以将概率P稍稍改造一下:令Q=P/(1-P),期望用Q作为z的现实意义。我们发现,当P的在区间[0,1]变化时,Q在[0,+∞)区间单调递增。函数图像如下(以下图像可以直接在度娘中搜“x/(1-x)”,超快):
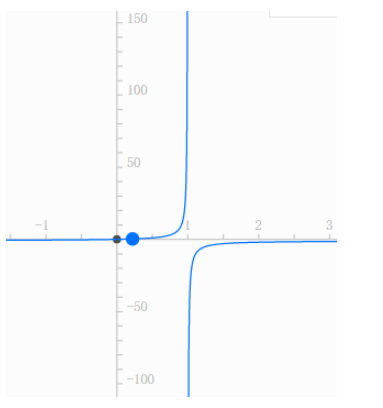
但是Q的变化率在[0,+∞)还不够,我们是希望能在(-∞,+∞)区间变化的。而且在P=1/2的时候刚好是0。这样才有足够的解释力。
注:因为P=1/2说明该点属于两个类别的可能性相当,也就是说这个点恰好在分界面上,那它在法向量的投影自然就是0了。
而在P=1/2时,Q=1,距离Q=0还有一段距离。那怎么通过一个函数变换然它等于0呢?有一个天然的函数log,刚好满足这个要求。
于是我们做变换R=log(Q)=log(P/(1-P)),期望用R作为z的现实意义。画出它的函数图像如图
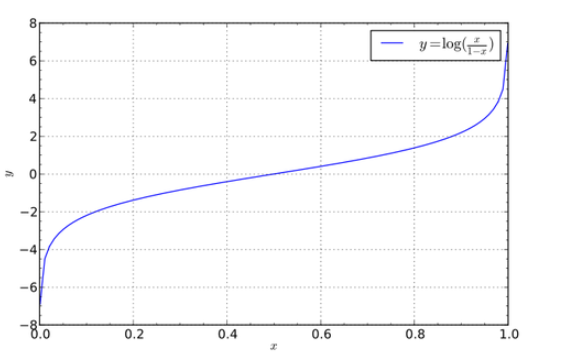
这个函数在区间[0,1]中可正可负可为零,单调地在(-∞,+∞)变化,而且1/2刚好就是唯一的0值!基本完美满足我们的要求。
回到我们本章最初的问题,
“我们由点x的坐标得到了一个新的特征z,那么z的具体意义是什么呢?”
由此,我们就可以将z理解成x属于y=1类的概率P经过某种变换后对应的值。也就是说,z= log(P/(1-P))。反过来就是P=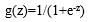 。图像如下:
。图像如下:
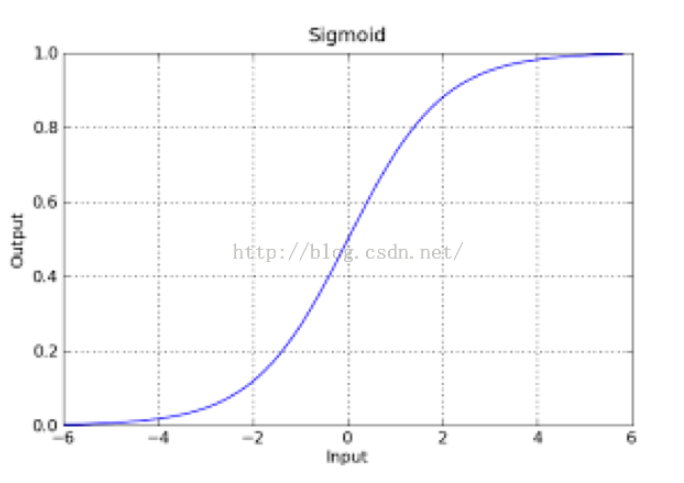
于是,我们不光得到了z的现实意义,还得到了z映射到概率P的拟合方程:
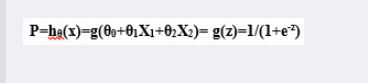
有了概率P,我们顺便就可以拿拟合方程P=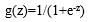 来判断点x所属的分类:
来判断点x所属的分类:
当P>=1/2的时候,就判断点x属于y=1的类别;当P<1/2,就判断点x属于y=0的类别。
4.构造代价函数求出参数的值
到目前为止我们就有两个判断某点所属分类的办法,一个是判断z是否大于0,一个是判断g(z)是否大于1/2。
然而这并没有什么X用,
以上的分析都是基于“假设我们已经找到了这条线”的前提得到的,但是最关键的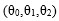 三个参数仍未找到有效的办法求出来。
三个参数仍未找到有效的办法求出来。
还有没有其他的性质可供我们利用来求出参数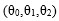 的值?
的值?
- 我们漏了一个关键的性质:这些样本点已经被标注了y=0或者y=1的类别!
- 我们一方面可以基于z是否大于0或者g(z) 是否大于1/2来判断一个点的类别,另一方又可以依据这些点已经被标注的类别与我们预测的类别的插值来评估我们预测的好坏。
- 这种衡量我们在某组参数下预估的结果和实际结果差距的函数,就是传说中的代价函数Cost Function。
- 当代价函数最小的时候,相应的参数
![(θ0,θ1,θ2)]() 就是我们希望的最优解。
就是我们希望的最优解。
由此可见,设计一个好的代价函数,将是我们处理好分类问题的关键。而且不同的代价函数,可能会有不同的结果。因此更需要我们将代价函数设计得解释性强,有现实针对性。
为了衡量**“预估结果和实际结果的差距”,我们首先要确定“预估结果”和“实际结果”**是什么。
- *“实际结果”**好确定,就是y=0还是y=1。
- “预估结果”有两个备选方案,经过上面的分析,我们可以采用z或者g(z)。但是显然g(z)更好,因为g(z)的意义是概率P,刚好在[0,1]范围之间,与实际结果{0,1}很相近,而z的意思是逻辑发生比,范围是整个实数域(-∞,+∞),不太好与y={0,1}进行比较。
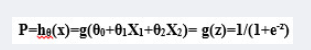
接下来是衡量两个结果的“差距”。
- 我们首先想到的是y-hθ(x)。
- 但这是当y=1的时候比较好。如果y=0,则y- hθ(x)= - hθ(x)是负数,不太好比较,则采用其绝对值hθ(x)即可。综合表示如下:
![]()
- 但这个函数有个问题:求导不太方便,进而用梯度下降法就不太方便。
- Andrew Ng在课程中直接给出了Cost函数及J(θ)函数如式(5)和(6),但是并没有给出具体的解释,只是说明了这个函数来衡量h函数预测的好坏是合理的
![]()
实际上这里的Cost函数和J(θ)函数是基于最大似然估计推导得到的。
概率论的知识告诉我们参数估计时可以采用最大似然法。假设有 m 个观测样本,观测值分别为 y1,y2,⋯,ym,设 为给定条件下得到 yi=1 的概率。同样地,yi=0 的概率为
为给定条件下得到 yi=1 的概率。同样地,yi=0 的概率为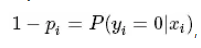
,所以得到一个观测值的概率为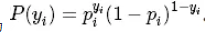 。
。
各个观测样本之间相互独立,那么它们的联合分布为各边缘分布的乘积。得到似然函数为
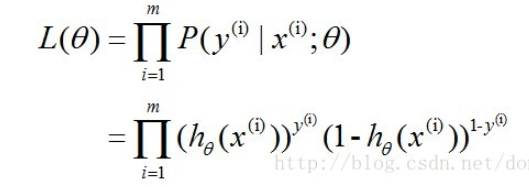
然后我们的目标是求出使这一似然函数值最大的参数估计,于是对函数取对数得到:(注:此处的W为上文的Thea,X为Z)
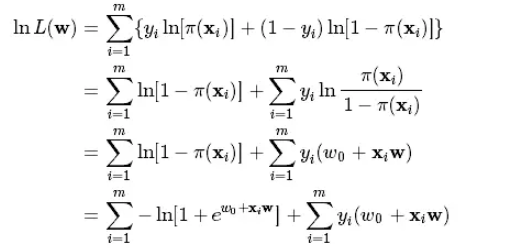
最大似然估计就是要求得使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将J(θ)取为(6)式,即:
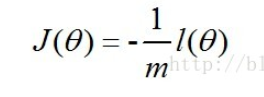
因为乘了一个负的系数-1/m,所以J(θ)取最小值时的θ为要求的最佳参数。
4.2使用梯度下降法求解参数
求J(θ)的最小值可以使用梯度下降法,根据梯度下降法可得θ的更新过程:
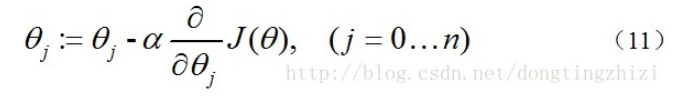
式中为α学习步长,下面来求偏导:
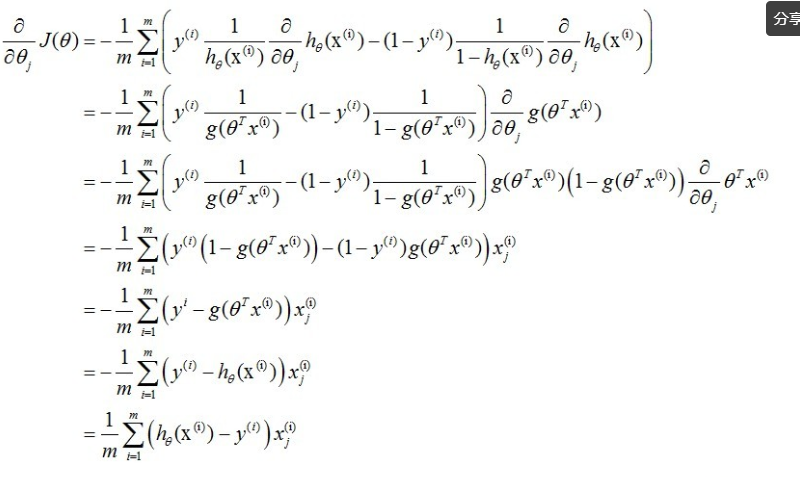
上式求解过程中用到如下的公式: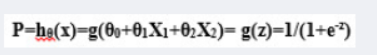

因此,(11)式的更新过程可以写成:
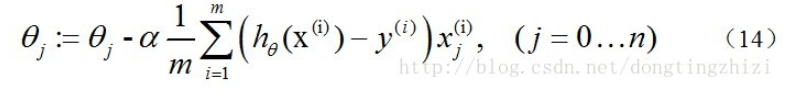
因为式中α本来为一常量,所以1/m一般将省略,所以最终的θ更新过程为:
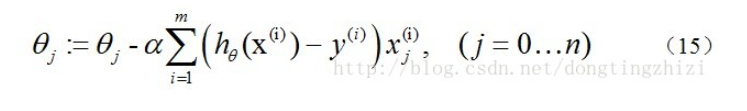
5.从特征处理的角度重新梳理我们刚才的分析过程
其实,做数据挖掘的过程,也可以理解成做特征处理的过程。我们典型的数据挖掘算法,也就是将一些成熟的特征处理过程给固定化的结果。
对于逻辑回归所处理的分类问题,我们已有的特征是这些点的坐标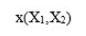 ,我们的目标就是判断这些点所属的分类y=0还是y=1。那么最理想的想法就是希望对坐标进行某种函数运算,得到一个(或者一些)新的特征z,基于这个特征z是否大于0来判断该样本所属的分类。
,我们的目标就是判断这些点所属的分类y=0还是y=1。那么最理想的想法就是希望对坐标进行某种函数运算,得到一个(或者一些)新的特征z,基于这个特征z是否大于0来判断该样本所属的分类。
对我们上一节非线性可分问题的推理过程进行进一步抽象,我们的思路其实是:
- 第一步,将点
![x(X1,X2]() 的坐标通过某种函数运算,得到一个新的类似逻辑发生比的特征,
的坐标通过某种函数运算,得到一个新的类似逻辑发生比的特征,![z=f(X1,X2)= X12+X22-r2]()
- 第二步是将特征z通过sigmoid函数得到新的特征
![q=g(z)= 1/(1+e-z)= 1/(1+e-f(X1,X2))]() 。
。 - 第三步是将所有这些点的特征q通过代价函数统一计算成一个值
![v=J(q1,q2,…)]() ,如果这是最小值,相应的参数®就是我们所需要的理想值。
,如果这是最小值,相应的参数®就是我们所需要的理想值。 ![]()
https://blog.csdn.net/XiaoXIANGZI222/article/details/55097570
https://blog.csdn.net/longxinchen_ml/article/details/49284391


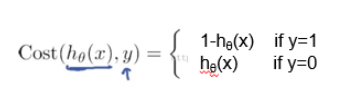
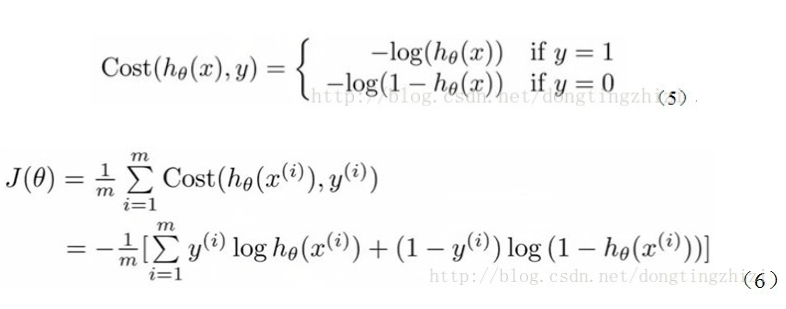
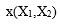 的坐标通过某种函数运算,得到一个新的类似逻辑发生比的特征,
的坐标通过某种函数运算,得到一个新的类似逻辑发生比的特征,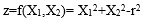
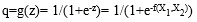 。
。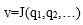 ,如果这是最小值,相应的参数®就是我们所需要的理想值。
,如果这是最小值,相应的参数®就是我们所需要的理想值。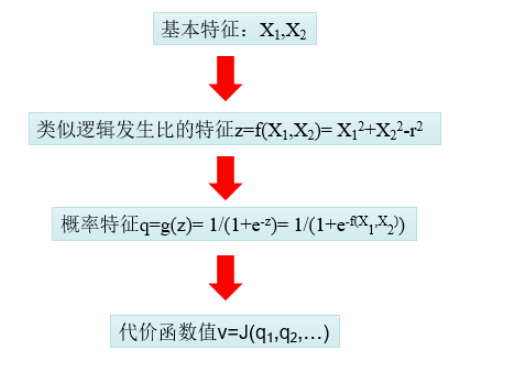

 浙公网安备 33010602011771号
浙公网安备 33010602011771号