【容斥原理】

【容斥原理】

计算多个集合的并集大小

公式

+ - + - + ...以此类推
若有A,B,C,D,E五个集合
则有并集个数

A+B+C+D+E
-(AB+AC+AD+AE+BC+BD+BE+CD+CE+DE)
+(ABC+ABD+ABE+BCD+BCE+CDE)
-(ABCD+ABCE+BCDE)
+ABCDE

题目整理

Count Good Numbers

https://codeforces.com/contest/2125/problem/C

题目大意

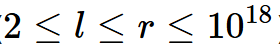
找l到r中质因子均为2位数以上的数字个数

思路

（1）均为2位数以上->把包含1位数质因子的数去掉就行
2,3,5,7
（2）求一个区间内k的倍数的数字个数floor(R)+floor(L-1)
->容斥即可

代码

i64 l,r;
void solve(){
    cin>>l>>r;
    i64 cnt1=r/2LL-(l-1LL)/2LL;
    i64 cnt2=r/3LL-(l-1LL)/3LL;
    i64 cnt3=r/5LL-(l-1LL)/5LL;
    i64 cnt4=r/7LL-(l-1LL)/7LL;
    i64 cnt5=r/6LL-(l-1LL)/6LL;
    i64 cnt6=r/10LL-(l-1LL)/10LL;
    i64 cnt7=r/14LL-(l-1LL)/14LL;
    i64 cnt8=r/15LL-(l-1LL)/15LL;
    i64 cnt9=r/21LL-(l-1LL)/21LL;
    i64 cnt10=r/35LL-(l-1LL)/35LL;
    i64 cnt11=r/30LL-(l-1LL)/30LL;
    i64 cnt12=r/42LL-(l-1LL)/42LL;
    i64 cnt13=r/70LL-(l-1LL)/70LL;
    i64 cnt14=r/105LL-(l-1LL)/105LL;
    i64 cnt15=r/210LL-(l-1LL)/210LL;
    i64 ans=cnt1+cnt2+cnt3+cnt4-cnt5-cnt6-cnt7-cnt8-cnt9-cnt10+cnt11+cnt12+cnt13+cnt14-cnt15;
    ans=(r-l+1)-ans;
    cout<<ans<<endl;
}