【三分】

【三分】

求单峰函数最大值/单谷函数最小值
凹函数/凸函数

思路

模版代码

整数域三分

求凸点

while (l < r) {
    int mid = (l + r) / 2;
    if (check(mid) >= check(mid + 1)) r = mid;
    else l = mid + 1;
}

求凹点

while (l < r) {
    int mid = (l + r) / 2;
    if (check(mid) <= check(mid + 1)) r = mid;
    else l = mid + 1;
}

实数域三分

求凸点

while(abs(r-l)>eps){//左右区间差值需要是一个很小的数
	ld mid=(l+r)/2;
	ld lmid=mid-eps;
	ld rmid=mid+eps;
	if(f(lmid)<f(rmid)) l=mid;//说明左区间需要被舍去
	else r=mid;//说明右区间需要被舍去
}
ld ans=(l+r)/2;

求凹点

while(abs(r-l)>eps){//左右区间差值需要是一个很小的数
	ld mid=(l+r)/2;
	ld lmid=mid-eps;
	ld rmid=mid+eps;
	if(f(ei,lmid)<f(ei,rmid)) r=mid;//说明左区间需要被舍去
	else l=mid;//说明右区间需要被舍去
}
ld k=(l+r)/2;

限制次数

//找凹点
ld l = -1e9, r = 1e9;
for (int t = 1; t <= 100; t++) {
    ld mid1 = (l * 2 + r) / 3;
    ld mid2 = (l + r * 2) / 3;
    if (judge(mid1) < judge(mid2)) {
        r = mid2;
    } else {
        l = mid1;
    }
}
cout << l << endl;
//找凸点
ld l = -1e9, r = 1e9;
for (int t = 1; t <= 100; t++) {
    ld mid1 = (l * 2 + r) / 3;
    ld mid2 = (l + r * 2) / 3;
    if (judge(mid1) > judge(mid2)) { 
        r = mid2;
    } else {
        l = mid1;
    }
}
cout << l << endl;

模版题

https://www.luogu.com.cn/problem/P3382

题目大意

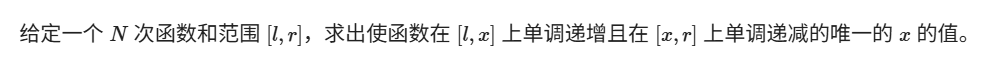
代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef long double ld;
typedef pair<int,int> PII;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int INF_INT=0x3f3f3f3f;
const ll INF_LL=0x3f3f3f3f3f3f3f3f;
const int N=20;
const ld eps=0.0000001;
int n;
ld l,r;
ld x[N];
ld f(ld a){
    ld aa=1;
    ld ans=0;
    for(int i=n;i>=0;i--){
        ans=ans+aa*x[i];
        aa=aa*a;
    }
    return ans;
}
void solve(){
    cin>>n;
    cin>>l>>r;
    //cout<<n<<endl;
    for(int i=0;i<=n;i++){
        cin>>x[i];
    }
    while(abs(r-l)>eps){
        ld mid=(l+r)/2;
        ld lmid=mid-eps;
        ld rmid=mid+eps;
        if(f(lmid)<f(rmid)) l=mid;
        else r=mid;
    }
    ld ans=(l+r)/2;
    cout<<fixed<<setprecision(6)<<ans<<endl;
}


signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int T=1;
    //cin>>T;
    while(T--) solve();
    return 0;
}

【题目积累】

【对勾函数】502 Bad Gateway

https://codeforces.com/gym/105358/problem/L

题目大意

思路

代码

struct Fraction {
private:
    i64 numerator;   // 分子
    i64 denominator; // 分母

    // 化简分数
    void reduce() {
        if (denominator == 0) {
            throw invalid_argument("分母不能为零");
        }

        // 确保分母为正数
        if (denominator < 0) {
            numerator *= -1;
            denominator *= -1;
        }

        // 约分
        i64 commonDivisor = gcd(numerator, denominator);
        if (commonDivisor != 0) {
            numerator /= commonDivisor;
            denominator /= commonDivisor;
        }

        // 分子为零时，分母固定为1
        if (numerator == 0) {
            denominator = 1;
        }
    }

public:
    // 构造函数
    Fraction(i64 num = 0, i64 den = 1) : numerator(num), denominator(den) {
        reduce();
    }

    // 拷贝构造函数
    Fraction(const Fraction& other) : numerator(other.numerator), denominator(other.denominator) {}

    // 判断是否为整数：分母为1时是整数
    bool isInteger() const {
        return denominator == 1;
    }

    // 加法运算
    Fraction operator+(const Fraction& other) const {
        i64 newDenominator = denominator * other.denominator;
        i64 newNumerator = numerator * other.denominator + other.numerator * denominator;
        return Fraction(newNumerator, newDenominator);
    }

    // 减法运算
    Fraction operator-(const Fraction& other) const {
        i64 newDenominator = denominator * other.denominator;
        i64 newNumerator = numerator * other.denominator - other.numerator * denominator;
        return Fraction(newNumerator, newDenominator);
    }

    // 乘法运算
    Fraction operator*(const Fraction& other) const {
        i64 newNumerator = numerator * other.numerator;
        i64 newDenominator = denominator * other.denominator;
        return Fraction(newNumerator, newDenominator);
    }

    // 除法运算
    Fraction operator/(const Fraction& other) const {
        if (other.numerator == 0) {
            throw invalid_argument("除数不能为零");
        }
        i64 newNumerator = numerator * other.denominator;
        i64 newDenominator = denominator * other.numerator;
        return Fraction(newNumerator, newDenominator);
    }

    // 赋值运算符
    Fraction& operator=(const Fraction& other) {
        if (this != &other) {
            numerator = other.numerator;
            denominator = other.denominator;
        }
        return *this;
    }

    // 输出运算符重载（友元函数）
    friend ostream& operator<<(ostream& os, const Fraction& f) {
        if (f.denominator == 1) {
            os << f.numerator;
        } else {
            os << f.numerator << " " << f.denominator;
        }
        return os;
    }

    // 获取分子
    i64 getNumerator() const { return numerator; }
    
    // 获取分母
    i64 getDenominator() const { return denominator; }
};
const int N=3e5+10;
i64 t;
ld check(i64 x){
    ld res=((ld)x-1.0)/2.0+(ld)t/ld(x);
    return res;
}
void solve(){
    cin>>t;
    i64 l=0,r=t;
    while (l < r) {
        i64 mid = (l + r) / 2;
        if (check(mid) <= check(mid + 1)) r = mid;
        else l = mid + 1;
    }
    Fraction f1(l-1LL,2LL);
    Fraction f2(t,l);
    Fraction ans=f1+f2;
    cout<<ans;
    if(ans.isInteger()) cout<<" "<<1;
    cout<<endl;
}