【贡献法】（数论）

【贡献法】（数论）

一般结合计数原理/组合数学

中位数

https://ac.nowcoder.com/acm/contest/111309/F

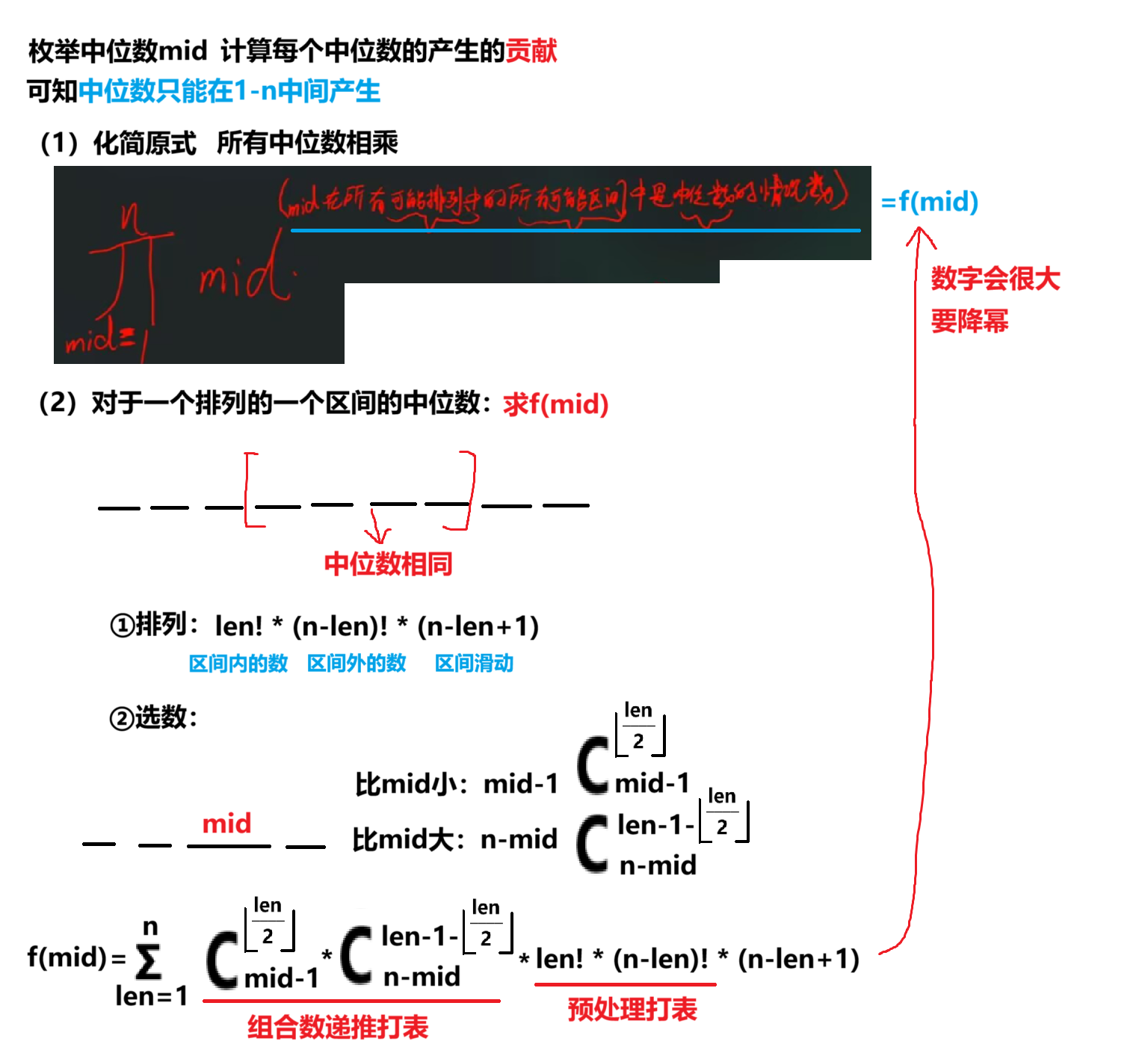
知识点：
（1）组合数递推打表
（2）降幂：费马小定理

注意在前面的取mod下取(mod-1)，在最后的操作上取mod（费马小定理逆运算）

const ll mod=1610612741;
const ll mod_phi=1610612740;
const int N=6e3+10;
ll add(ll x,ll y,ll mod){
    ll res=(x+y)%mod;
    return res;
}
ll qmi(ll a,ll k,ll p){
    ll ans=1;
    while(k){
        if(k&1) ans=ans*a%p;
        k>>=1;
        a=a*a%p;
    }
    return ans;
}
ll n;
ll C[N][N],f[N];
void init(){
    f[0]=1LL;
    for(int i=1;i<=6e3;i++){
        if(i==1) f[i]=1LL;
        f[i]=f[i-1]*(ll)i%mod_phi;
    }
    for(int i=0;i<=6e3;i++){
        C[i][0]=1LL;
        C[i][i]=1LL;
        for(int j=1;j<i;j++){
            C[i][j]=add(C[i-1][j-1],C[i-1][j],mod_phi);
        }
    }
}
void solve(){
    cin>>n;
    ll ans=1LL;
    for(int mid=2;mid<=n;mid++){
        ll tot=0;
        for(int len=1;len<=n;len++){
            int x=len/2,y=len-x-1;
            int p=mid-1,q=n-mid;
            ll cnt=(C[p][x]*C[q][y])%mod_phi;
            cnt=(cnt*f[len])%mod_phi;
            cnt=(cnt*f[n-len])%mod_phi;
            cnt=(cnt*((ll)n-(ll)len+1LL))%mod_phi;
            tot=add(tot,cnt,mod_phi);
        }
        ans=(ans*qmi((ll)mid,tot,mod))%mod;
    }
    cout<<ans<<endl;
}