【一欧元滤波器】

【一欧元滤波器】

用于实时噪声过滤的低通滤波器

作用

姿态消抖：关键点高频抖动

指数平滑法

一种平均法
基于一定的时间序列，随着数据的远离，赋予逐渐收敛为零的权数

一次指数平滑预测

平滑系数a 初值Y0
公比(1-a)
平滑系数a越小，平滑作用越强，但对实际数据的变动反应较迟缓

大致原理

利用在低速时对抖动更敏感，而高速时对滞后更敏感的特点

主要参数：最小截止频率，速度系数

mincutoff 最小截止频率
该值越小，平滑效果越明显，但滞后也会越大。
beta 速度系数
用于控制截止频率随信号变化率的增加而增加的速度
较大的 beta 值能让滤波器在信号快速变化时更迅速地响应，减少滞后，但同时也会引入更多噪声。
dcutoff 导数截止频率
用于平滑信号的变化率估计，可减少因噪声引起的变化率估计误差

数学公式

滤波公式

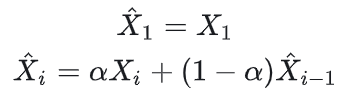
这一阶段滤波值=这一阶段观测值+上一阶段滤波值

自适应平滑因子

求α

Te：采样频率 一般是固定的

平滑速度

调节参数

freq采样频率

较高的 freq 会使滤波器更能及时响应信号的变化、
过高的 freq 会增加计算量，并且如果信号本身没有那么高的变化频率，还可能引入更多噪声。

mincutoff最小截止频率

较低的 mincutoff 可以让更多低频信号通过，使滤波器更平滑，适合处理变化缓慢的信号。
但如果设置得过低，可能会引入更多噪声。

beta平滑因子

概念上
控制截止频率随信号变化率（导数）的调整幅度。
当信号变化剧烈时，beta 会使截止频率相应提高，允许更高频率的信号通过滤波器
信号变化缓慢时，截止频率则接近 mincutoff
调参上
过大的 beta 会让滤波器过度响应噪声，使滤波结果波动较大
较小的 beta 值会使滤波器更平滑，但在信号快速变化时可能会出现滞后现象

dcutoff默认截止频率

过高的 dcutoff 会让截止频率频繁波动，使滤波结果不准确
设置得过低，会使滤波器对信号变化的响应变慢

代码实现

import math

# 【滤波流程】
# （1）根据默认截止频率(dcutoff)求平滑后的[一阶导数]
#  速度求法：(这次数据-上次数据)/采样时间
# （2）求出实际截止频率：最小截止频率+平滑因子*|平滑后的一阶导数|

# 【调参建议】低通滤波：无论如何调节不会超过Noisy值
# （1）freq：越大 越远离噪声值 越小逼近速度更快
# （2）mincutoff最小截止频率：越大 越接近噪声值 逼近速度越快
# （3）beta平滑因子：越大 越接近噪声值 逼近速度越快
# （4）dcutoff默认截止频率：轻微调节滤波值逼近噪声值

class OneEuroFilter:
    def __init__(self, freq, mincutoff=1.0, beta=0.0, dcutoff=1.0):
        self.freq = freq # 采样频率
        self.mincutoff = mincutoff
        self.beta = beta
        self.dcutoff = dcutoff
        self.x_prev = None
        self.dx_prev = 0

    def alpha(self, cutoff):
        te = 1.0 / self.freq #求采样时间：1/采样频率
        tau = 1.0 / (2 * math.pi * cutoff) # T
        return 1.0 / (1.0 + tau / te)

    def filter(self, x):
        if self.x_prev is None:
            dx = 0
        else:
            dx = (x - self.x_prev) * self.freq
        edx = self.alpha(self.dcutoff) * dx + (1 - self.alpha(self.dcutoff)) * self.dx_prev
        # 求截止频率：最小截止频率+速度系数*平滑后速度
        cutoff = self.mincutoff + self.beta * abs(edx)
        x_filtered = self.alpha(cutoff) * x + (1 - self.alpha(cutoff)) * (
            self.x_prev if self.x_prev is not None else x)
        self.x_prev = x_filtered
        self.dx_prev = edx
        return x_filtered


# 示例使用
if __name__ == "__main__":
    # 模拟一个带噪声的信号
    noisy_signal = [i + (i % 3 - 1) * 0.5 for i in range(20)]
    # 初始化单欧元滤波器
    freq = 10  # 采样频率
    filter = OneEuroFilter(freq, mincutoff=1.0, beta=0.05, dcutoff=1.0)
    # 对信号进行滤波
    filtered_signal = [filter.filter(x) for x in noisy_signal]

    print("Noisy signal:", noisy_signal)
    print("Filtered signal:", filtered_signal)