【线段树】
【线段树】
Segment Tree
使用场景
只要满足区间可加性(大区间的信息能由它的两个子区间整理得到)
可以在 O(logN) 的时间复杂度内实现:
单点修改、区间修改、区间查询(区间求和,求区间最大值,求区间最小值) 等
模版代码
【区间修改(加法),区间最值/和】
// 线段树模板类,支持泛型类型T
template<class T>
struct Segt {
// 线段树节点结构
struct node {
int l, r; // 当前节点覆盖的区间 [l, r]
T w; // 区间和
T rmq; // 区间最值(最小/最大值)
T lazy; // 懒标记,用于区间更新优化
bool has_lazy; // 标记是否有未下推的懒标记
};
vector<T> w; // 存储原始数据
vector<node> t; // 存储线段树节点
// 构造函数
Segt() {}
Segt(int n) { init(n); }
// 从向量初始化线段树
Segt(vector<i64> in) {
int n = in.size() - 1;
w.resize(n + 1);
for (int i = 1; i <= n; i++) {
w[i] = in[i];
}
init(in.size() - 1);
}
// 宏定义:左孩子和右孩子的索引计算
#define GL (k << 1) // 左孩子:k*2
#define GR (k << 1 | 1) // 右孩子:k*2+1
// 初始化线段树
void init(int n) {
w.resize(n + 1);
t.resize(n * 4 + 1); // 线段树通常需要4*n的空间
// 递归构建线段树
auto build = [&](auto self, int l, int r, int k = 1) {
if (l == r) { // 叶子节点,对应单个元素
// 初始化叶子节点:区间和=元素值,最小值=元素值,无懒标记
t[k] = {l, r, w[l], w[l], 0, false};
return;
}
t[k] = {l, r, 0, 0, 0, false}; // 初始化非叶子节点
int mid = (l + r) / 2; // 计算中间点,划分左右区间
self(self, l, mid, GL); // 递归构建左子树
self(self, mid + 1, r, GR); // 递归构建右子树
pushup(k); // 上传子节点信息到当前节点
};
build(build, 1, n); // 从根节点(1)开始构建,覆盖区间[1, n]
}
// 带参数的下推函数:将懒标记应用到当前节点
void pushdown(node &p, T lazy) {
p.w += (p.r - p.l + 1) * lazy; // 更新区间和
p.rmq += lazy; // 更新区间最值
p.lazy += lazy; // 累加懒标记值
p.has_lazy = true; // 标记有未下推的懒标记
}
// 下推函数:将当前节点的懒标记传递给子节点
void pushdown(int k) {
if (!t[k].has_lazy) return; // 没有懒标记则不需要下推
// 将懒标记下推到左右孩子
pushdown(t[GL], t[k].lazy);
pushdown(t[GR], t[k].lazy);
// 清除当前节点的懒标记
t[k].lazy = 0;
t[k].has_lazy = false;
}
// 上传函数:用子节点的信息更新当前节点
void pushup(int k) {
auto pushup = [&](node &p, node &l, node &r) {
p.w = l.w + r.w; // 区间和 = 左子树和 + 右子树和
p.rmq = min(l.rmq, r.rmq); // 区间最值 = 左右子树最小值的较小者
};
pushup(t[k], t[GL], t[GR]); // 更新当前节点
}
// 区间修改:将[l, r]区间内的每个元素加上val
void modify(int l, int r, T val, int k = 1) {
// 如果当前节点的区间完全在目标区间内
if (l <= t[k].l && t[k].r <= r) {
pushdown(t[k], val); // 应用修改到当前节点并更新懒标记
return;
}
pushdown(k); // 下推懒标记,确保子节点数据正确
int mid = (t[k].l + t[k].r) / 2; // 计算中间点
if (l <= mid) modify(l, r, val, GL); // 递归修改左子树
if (mid < r) modify(l, r, val, GR); // 递归修改右子树
pushup(k); // 更新当前节点信息
}
// 区间询问最值:查询[l, r]区间内的最小值
T rmq(int l, int r, int k = 1) {
// 如果当前节点的区间完全在目标区间内,直接返回当前节点的最小值
if (l <= t[k].l && t[k].r <= r) {
return t[k].rmq;
}
pushdown(k); // 下推懒标记,确保子节点数据正确
int mid = (t[k].l + t[k].r) / 2; // 计算中间点
T ans = numeric_limits<T>::max(); // 初始化答案为最大值
// 递归查询左子树
if (l <= mid) ans = min(ans, rmq(l, r, GL));
// 递归查询右子树
if (mid < r) ans = min(ans, rmq(l, r, GR));
return ans; // 返回区间最小值
}
// 区间询问和:查询[l, r]区间内的元素和
T ask(int l, int r, int k = 1) {
// 如果当前节点的区间完全在目标区间内,直接返回当前节点的区间和
if (l <= t[k].l && t[k].r <= r) {
return t[k].w;
}
pushdown(k); // 下推懒标记,确保子节点数据正确
int mid = (t[k].l + t[k].r) / 2; // 计算中间点
T ans = 0; // 初始化答案为0
// 递归查询左子树并累加结果
if (l <= mid) ans += ask(l, r, GL);
// 递归查询右子树并累加结果
if (mid < r) ans += ask(l, r, GR);
return ans; // 返回区间和
}
// 调试函数:打印线段树的结构和节点信息
void debug(int k = 1) {
cout << "[" << t[k].l << ", " << t[k].r << "]: ";
cout << "w = " << t[k].w << ", ";
cout << "Min = " << t[k].rmq << ", ";
cout << "lazy = " << t[k].lazy << ", ";
cout << "has_lazy = " << t[k].has_lazy << endl;
if (t[k].l == t[k].r) return; // 叶子节点则停止递归
debug(GL), debug(GR); // 递归打印左右子树
}
};
模版题
区间最值 https://www.luogu.com.cn/problem/P1816
区间修改+区间求和 https://www.luogu.com.cn/problem/P3372
https://www.luogu.com.cn/problem/P3373
线段树推导
五个基本要素:信息存储,建树,单点修改,区间查询,区间修改

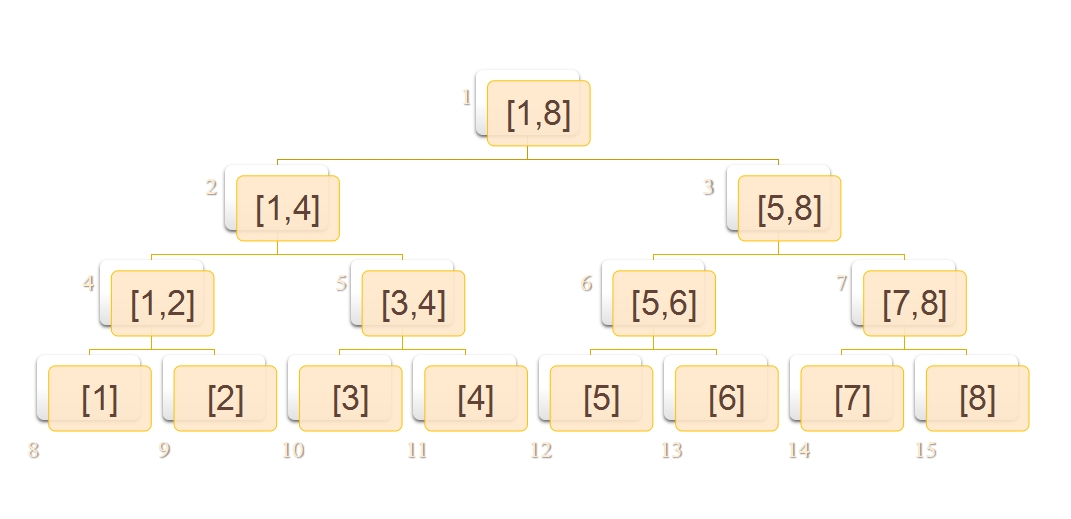
->堆排序方式存点
存储信息

数组要开4N
struct SegmentTree {
int l, r;//每个区间左右端点
int dat;//区间数据
int tag;//懒标记
//其他一些附加信息
}tree[4*MAX];
建树
从根节点“1”出发,向下递归建树,并把每个节点所代表的区间赋给它。
当到达了叶节点,便传值,再向上维护信息
【pushup操作】
void pushup(int x){//更新线段树 x 号节点
tr[x]=tr[2*x]+tr[2*x+1];//tr 为线段树数组
}
//以区间和为例
void build(int x,int l,int r){
if(l==r) tr[x]=a[l];
else{
int mid=(l+r)/2;
build(2*x,l,mid);//更新左儿子
build(2*x+1,mid+1,r);//更新右儿子
pushup(x);
}
}
单点修改
从根节点开始遍历,递归找到需要修改的叶子节点,然后修改,然后向上传递信息
如果 k 位于左儿子维护区间(<=mid),递归更新左儿子,右儿子同理
如果当前节点为叶子结点,更新该节点的值加上v
时间复杂度O(logN)
//第k个数增加v
void update(int x,int l,int r,int k,int v){
if(l==r&&l==k){
tr[x]+=v;
return ;
}
if(k<=mid) update(2*x,l,mid,k,v);
else update(2*x+1,mid+1,r,k,v);
pushup(x);
}
区间查询
(不加懒标记)
1.若当前节点所表示的区间已经被询问区间所完全覆盖,则立即回溯,并传回该点的信息。
2.若当前节点的左儿子所表示的区间已经被询问区间所完全覆盖,就递归访问它的左儿子。
3.若当前节点的右儿子所表示的区间已经被询问区间所完全覆盖,就递归访问它的右儿子。
int query(int x,int l,int r,int from,int to){
int ans=0;
if(from<=l&&r<=to) return tr[x];
if(from<=mid) ans+=query(2*x,l,mid,from,to);
if(to>mid) ans+=query(2*x+1,mid+1,r,from,to);
return ans;
}
懒标记
【延迟更新】
当区间修改把一个区间修改完之后,如果要往下一直递归修改,时间复杂度会爆掉。
在这个节点打一个标记v:现在这个节点的子树(除该节点本身)维护的值比实际的值少v
下一次需要用到这个节点的子节点的维护值时,再把两个子节点的维护值更新,并且将该节点的懒标记清空
将两个子节点的懒标记加上原来父节点的懒标记值(这两个子节点的四个子节点现在比她们的父节点又少了v)
区间修改
【pushdown操作】
void pushdown(int x,int l,int r){
if(l==r) return;
//加上原来父节点的懒标记值
tr[2*x].sum+=(mid-l+1)*tr[x].tag;
tr[2*x+1].sum+=(r-mid)*tr[x].tag;
//将懒标记下放
tr[2*x].tag+=tr[x].tag; //注意这里需要 + 而不是直接赋值
tr[2*x+1].tag+=tr[x].tag;
//去掉父节点的懒标记
tr[x].tag=0;
}
【区间更新】
//将[from,to]区间加上v
void update(int x,int l,int r,int from,int to,int v){
if(from<=l&&r<=to){
tr[x].sum+=(r-l+1)*v;//区间长度*更新值
tr[x].tag+=v;
return ;
}
pushdown(x,l,r);//更新懒标记与子节点的值
if(from<=mid) update(2*x,l,mid,from,to,v);
if(to>mid) update(2*x+1,mid+1,r,from,to,v);
pushup(x);
}
此时的 【区间查询】 也需要用到懒标记
int query(int x,int l,int r,int from,int to){
int ans=0;
if(from<=l&&r<=to) return tr[x];
//先往下传懒标记
pushdown(x,l,r);
if(from<=mid) ans+=query(2*x,l,mid,from,to);
if(to>mid) ans+=query(2*x+1,mid+1,r,from,to);
return ans;
}
板子题
最大数
https://www.acwing.com/problem/content/1277/
注意本题强制在线
且要开ll
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=200010;
int m,p;
struct Node{
int l,r;
int v;//区间[l,r]的最大值
}tr[N*4];
//pushup基本操作
void pushup(int u){
tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}
//建树
void build(int u,int l,int r){
tr[u]={l,r};
if(l==r) return;
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
}
//查询
int query(int u,int l,int r){
if(tr[u].l>=l && tr[u].r<=r) return tr[u].v;//树中节点,已经被完全包含在[l,r]中
int mid=tr[u].l+tr[u].r>>1;
int v=0;
if(l<=mid) v=query(u<<1,l,r);
//求最大值
if(r>mid) v=max(v,query(u<<1|1,l,r));
return v;
}
//修改
void modify(int u,int x,int v){
if(tr[u].l==tr[u].r) tr[u].v=v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
ll n=0,last=0;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>m>>p;
build(1,1,m);
ll x;//注意要开ll:2e9会爆
string op;
while(m--){
cin>>op>>x;
if(op=="Q"){
last=query(1,n-x+1,n);
cout<<last<<endl;
}
else if(op=="A"){
modify(1,n+1,(last+x)%p);
n++;
}
}
return 0;
}
参考:
https://www.cnblogs.com/silentEAG/p/10808978.html
https://oi-wiki.org/ds/seg/
https://www.luogu.com.cn/article/p8hyxnl7


 浙公网安备 33010602011771号
浙公网安备 33010602011771号