【前缀和】
【前缀和】
难点在于推公式
构造矩形
https://ac.nowcoder.com/acm/contest/102742/E
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=1e5+10;
/*
【前缀和推公式】
考虑(a[j]-a[i])作为长和作为宽的情况
作为长:宽的个数应该是m-(a[j]-a[i]-k)+1
【将i固定】
->考虑左右边界:(a[j]-a[i])>k 且 m-(a[j]-a[i]-k)+1>0 ->j同时有左边界和右边界
作为宽:长的个数应该是m-(a[j]-a[i]+k)+1
->考虑左右边界:m-(a[j]-a[i]+k)+1>0->j有右边界
->①二分找左右边界
->可前缀和优化求和公式:降一维复杂度
*/
int n,m;
ll k;
ll a[N];
ll s[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
s[i]=s[i-1]+a[i];
}
ll ans=0;
for(int i=1;i<n;i++){
//作为长
//找左边界
int l=i+1,r=n+1;
while(l<r){
int mid=(l+r)>>1;
if(a[mid]-a[i]>k) r=mid;
else l=mid+1;
}
if(l<n+1){
//找右边界
int L=r;
l=i;r=n;
while(l<r){
int mid=(l+r+1)>>1;
if(m-(a[mid]-a[i]-k)+1>0) l=mid;
else r=mid-1;
}
if(r>i){
int R=l;
ans+=(ll)m*(R-L+1)-(((s[R]-s[L-1])-a[i]*(R-L+1))-k*(R-L+1))+(R-L+1);
//cout<<L<<" "<<R<<endl;
}
}
//作为宽
l=i;r=n;
while(l<r){
int mid=(l+r+1)>>1;
if(m-(a[mid]-a[i]+k)+1>0) l=mid;
else r=mid-1;
}
if(r>i){
int cnt=l;
//cout<<cnt<<endl;
//注意要防止爆int
ans+=(ll)m*(cnt-i)-(((s[cnt]-s[i])-a[i]*(cnt-i))+k*(cnt-i))+(cnt-i);
}
}
cout<<ans;
return 0;
}
卡牌游戏
https://qoj.ac/contest/2182/problem/12369
题目大意
奇数位置和偶数位置上的数的和取最小值
现可以选择一个位置,把他插到其他位置,位置奇偶性会改变
问最后取值的最大值是多少
思路

代码
int n;
void solve(){
cin>>n;
vector<i64> a(2*n+1,0);
for(int i=1;i<=2*n;i++) cin>>a[i];
vector<vector<i64>> s(2,vector<i64>(2*n+1,0));
set<i64> st[2];
//求奇偶前缀和
for(int i=1;i<=2*n;i++){
s[0][i]=s[0][i-1]+((i%2==0)?a[i]:0);
s[1][i]=s[1][i-1]+((i%2==1)?a[i]:0);
}
i64 ans=min(s[0][2*n],s[1][2*n]),d=(s[0][2*n]-s[1][2*n])/2;
//目标是能找到s[0][2*n]-d,s[1][2*n]+d
for(int i=1;i<=2*n;i++){
i64 tar=s[0][i]-s[1][i]-d,v=i%2;//v奇偶性 tar是要在set里找的值
//找接近的:set找最大的最小,最小的最大
auto t=st[v].lower_bound(tar);
if(t!=st[v].end()){
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
if(st[v].size() && t!=st[v].begin()){
--t;
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
tar=s[0][i]-s[1][i]-(d+1),v=i%2;
t=st[v].lower_bound(tar);
if(t!=st[v].end()){
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
if(st[v].size() && t!=st[v].begin()){
--t;
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
tar=s[0][i]-s[1][i]-(d-1),v=i%2;
t=st[v].lower_bound(tar);
if(t!=st[v].end()){
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
if(st[v].size() && t!=st[v].begin()){
--t;
i64 res=*t;
i64 now=s[0][i]-s[1][i]-res;
ans=max(ans,min(s[0][2*n]-now,s[1][2*n]+now));
}
st[(i-1)%2].insert(s[0][i-1]-s[1][i-1]);
}
cout<<ans<<endl;
}
前缀异或
异或和之和
https://www.lanqiao.cn/problems/3507/learning/
前缀异或:拆开每一位看贡献
/*【前缀和优化】
ll sum=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
sum+=s[i]^s[j-1];
}
}
->有没有办法去掉一维?
->位运算:考虑枚举每一位
->在每一位下求前缀异或:选择i和j-1,只有0和1组合才能产生贡献
->统计每一位下0和1的个数->乘法原理
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n;
int a[N];
int s[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
ll ans=0;
for(int k=0;k<=20;k++){
s[0]=0;
int zero=1,one=0;//初始为0
for(int i=1;i<=n;i++){
int t=(a[i]>>k)&1;
s[i]=s[i-1]^t;
if(s[i]==1) one++;
else zero++;
}
ll res=(ll)one*zero*(1<<k);
ans+=res;
}
cout<<ans;
return 0;
}
XOR Array
https://codeforces.com/contest/2175/problem/B
题目大意

思路
考虑前缀异或:\(b_y \otimes b_{x-1} = 0\)
那么构造\(b_i=i\),仅\(b_r=l-1\)
前缀异或还原成原数组公式:\(a_i=b_i \otimes b_{i-1}\)
思路
int n,l,r;
void solve(){
cin>>n>>l>>r;
vector<int> a(n+2,0);
int idx=1;
for(int i=1;i<=n;i++){
a[i]=i;
}
a[r]=l-1;
vector<int> b(n+2,0);
for(int i=1;i<=n;i++){
b[i]=a[i]^a[i-1];
}
for(int i=1;i<=n;i++){
cout<<b[i]<<" ";
}
cout<<endl;
}
Tail of Snake
https://atcoder.jp/contests/abc438/tasks/abc438_d
关注下标
题目大意
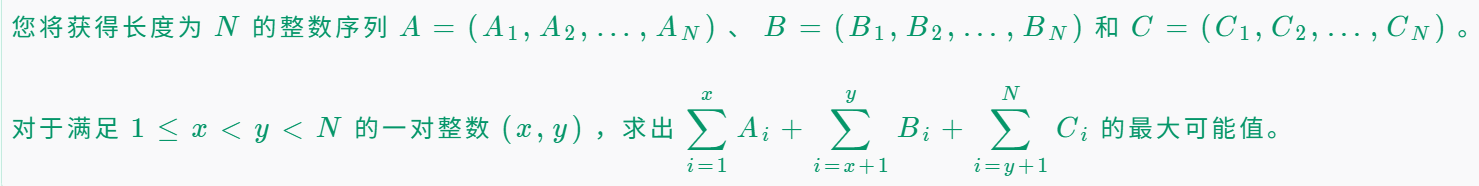
思路
错误解法:遍历x,y三分->注意这里无三分性质(有多峰,不单调,有负数值)
正确解法:前缀和公式转化
ans
=as[x]+bs[y]-bs[x]+cs[n]-cs[y]
=(as[x]-bs[x])+(bs[y]-cs[y])+cs[n]
那么在1<=x<y<n的情况下,遍历(bs[y]-cs[y]),找(as[x]-bs[x])最小值。
代码
int n;
void solve(){
cin>>n;
vector<i64> a(n+1,0),b(n+1,0),c(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<=n;i++) cin>>c[i];
vector<i64> as(n+1,0),bs(n+1,0),cs(n+1,0);
for(int i=1;i<=n;i++) as[i]=as[i-1]+a[i];
for(int i=1;i<=n;i++) bs[i]=bs[i-1]+b[i];
for(int i=1;i<=n;i++) cs[i]=cs[i-1]+c[i];
vector<i64> x(n+1,0),y(n+1,0);
for(int i=1;i<=n;i++){
x[i]=as[i]-bs[i];
}
for(int i=1;i<=n;i++){
y[i]=bs[i]-cs[i];
}
vector<i64> xmx(n+1,-1e18);
xmx[1]=x[1];
for(int i=1;i<=n;i++){
xmx[i]=whink_max<i64>(xmx[i-1],x[i]);
}
i64 ans=-1e18;
//注意这里初始化最小值要给最小!(as[x]-bs[x])、(bs[y]-cs[y])均有可能为负值
for(int i=2;i<=n-1;i++){
i64 res=cs[n]+xmx[i-1]+y[i];
ans=whink_max<i64>(ans,res);
}
cout<<ans<<endl;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号