【组合数学】

【组合数学】

一般是推公式

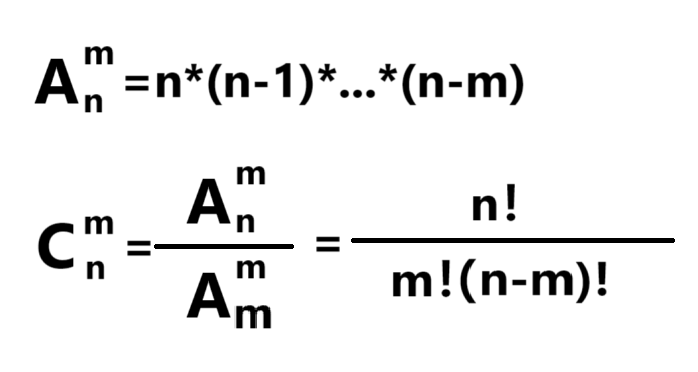
模版代码

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int MOD = 1e9 + 7;  // 定义模数
const int MAX = 1e6 + 10;
ll fact[MAX];      // 存储阶乘
ll inv_fact[MAX];  // 存储阶乘的逆元
// 快速幂
ll pow_mod(ll a, ll b) {
      ll res = 1;
      while (b) {
            if (b & 1) res = res * a % MOD;
            a = a * a % MOD;
            b >>= 1;
      }
      return res;
}
//预处理阶乘和逆元
void precompute() {
      fact[0] = 1;
      for (int i = 1; i < MAX; ++i) {
            fact[i] = fact[i - 1] * i % MOD; // 计算阶乘
      }
      inv_fact[MAX - 1] = pow_mod(fact[MAX - 1], MOD - 2); // 计算最大阶乘的逆元
      for (int i = MAX - 2; i >= 0; --i) {
            inv_fact[i] = inv_fact[i + 1] * (i + 1) % MOD; // 递推计算逆元
      }
}
//使用时记得反过来！
// 计算组合数 C(n, k)
ll C(int n, int k) {
      if (n < 0 || k < 0 || n < k) return 0; // 边界条件
      return fact[n] * inv_fact[k] % MOD * inv_fact[n - k] % MOD;
}
// 计算排列数 A(n, k)
ll A(int n, int k) {
      if (n < 0 || k < 0 || n < k) return 0; // 边界条件
      return fact[n] * inv_fact[n - k] % MOD;
}

注意点

（1）记得C和A函数里的对应式子是反过来的！（前大后小）
（2）记得main里要先处理阶乘和逆元！

组合数表

当n<=1e4的时候用
利用C[i][j]=(C[i-1][j]+C[i-1][j-1])性质

ll C[N][N],f[N];
void init(){
    f[0]=1LL;
    for(int i=1;i<=6e3;i++){
        if(i==1) f[i]=1LL;
        f[i]=f[i-1]*(ll)i%mod_phi;
    }
    for(int i=0;i<=6e3;i++){
        C[i][0]=1LL;
        C[i][i]=1LL;
        for(int j=1;j<i;j++){
            C[i][j]=add(C[i-1][j-1],C[i-1][j],mod_phi);
        }
    }
}

题目整理

小红的好排列

https://ac.nowcoder.com/acm/contest/100902/E

思路

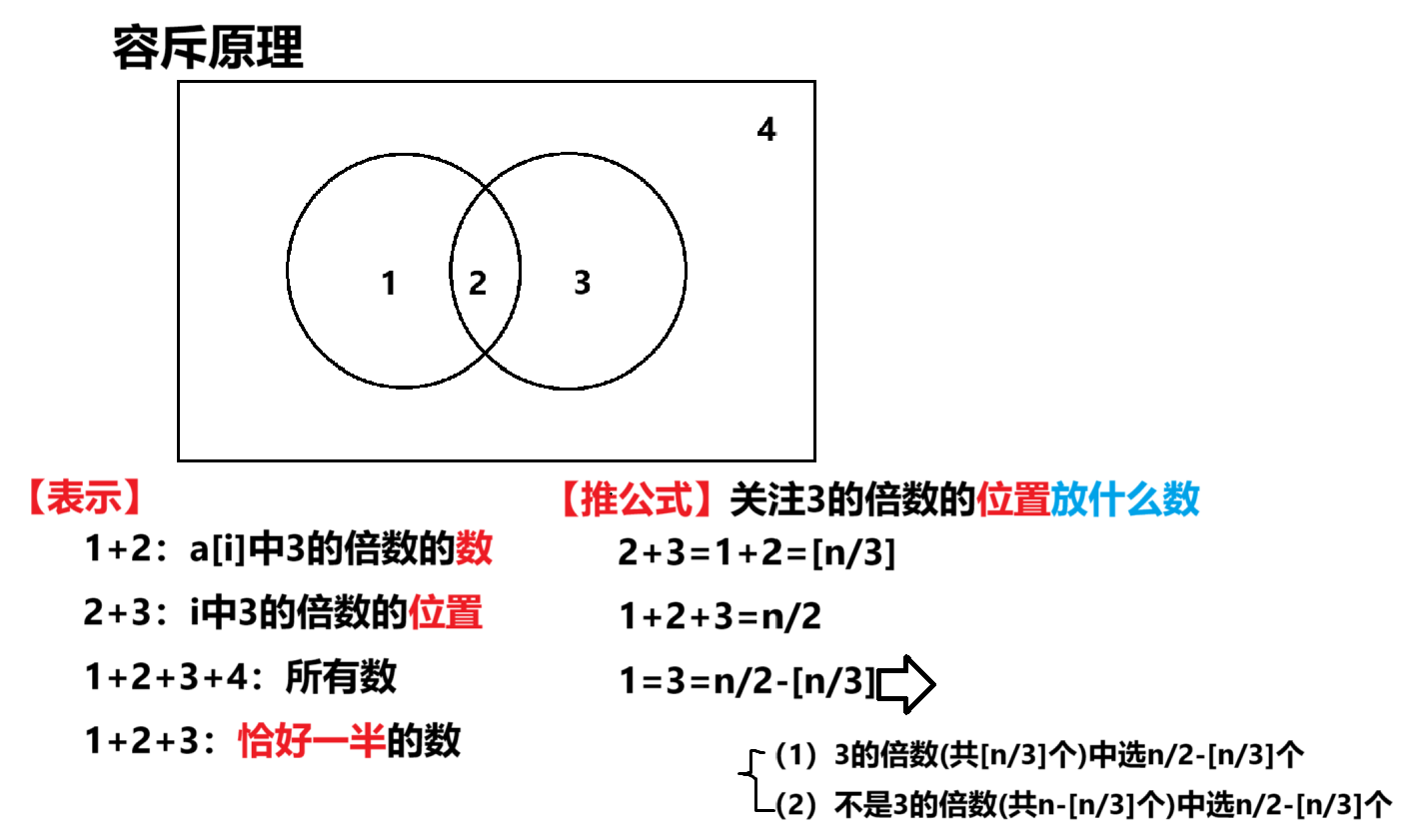
->公式

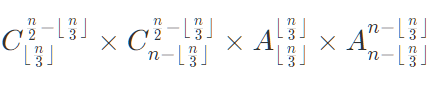
代码

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int MOD = 1e9 + 7;  // 定义模数
const int MAX = 1e6 + 10;
ll fact[MAX];      // 存储阶乘
ll inv_fact[MAX];  // 存储阶乘的逆元
// 快速幂
ll pow_mod(ll a, ll b) {
      ll res = 1;
      while (b) {
            if (b & 1) res = res * a % MOD;
            a = a * a % MOD;
            b >>= 1;
      }
      return res;
}
//预处理阶乘和逆元
void precompute() {
      fact[0] = 1;
      for (int i = 1; i < MAX; ++i) {
            fact[i] = fact[i - 1] * i % MOD; // 计算阶乘
      }
      inv_fact[MAX - 1] = pow_mod(fact[MAX - 1], MOD - 2); // 计算最大阶乘的逆元
      for (int i = MAX - 2; i >= 0; --i) {
            inv_fact[i] = inv_fact[i + 1] * (i + 1) % MOD; // 递推计算逆元
      }
}
// 计算组合数 C(n, k)
ll C(ll n, ll k) {
      if (n < 0 || k < 0 || n < k) return 0; // 边界条件
      return fact[n] * inv_fact[k] % MOD * inv_fact[n - k] % MOD;
}
// 计算排列数 A(n, k)
ll A(ll n, ll k) {
      if (n < 0 || k < 0 || n < k) return 0; // 边界条件
      return fact[n] * inv_fact[n - k] % MOD;
}
ll n;
int main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>n;
      //记得预处理阶乘和逆元！
      precompute();
      ll cnt1=n/2;
      ll cnt2=n/3;
      //这里注意要一个一个乘过去取模->会爆ll
      ll ans=C(cnt2,cnt1-cnt2);
      ans=ans*C(n-cnt2,cnt1-cnt2)%MOD;
      ans=ans*A(cnt2,cnt2)%MOD;
      ans=ans*A(n-cnt2,n-cnt2)%MOD;
      cout<<ans;
      return 0;
}

小红开灯（三，easy）

https://ac.nowcoder.com/acm/contest/107000/C
一共(n-k+1)个区间->每个区间都有选or不选2种状态
->乘法原理 2^(n-k+1)

const ll mod=1e9+7;
ll n,k;
ll qmi(ll a,ll k,ll p){
    ll res=1;
    while(k>0){
        if(k&1) res=res*a%p;
        k>>=1;
        a=a*a%p;
    }
    return res;
}
void solve(){
    cin>>n>>k;
    ll ans=qmi(2LL,(n-k+1),mod);
    cout<<ans;
}