【快速幂】
【快速幂】
运用
求a^k mod p

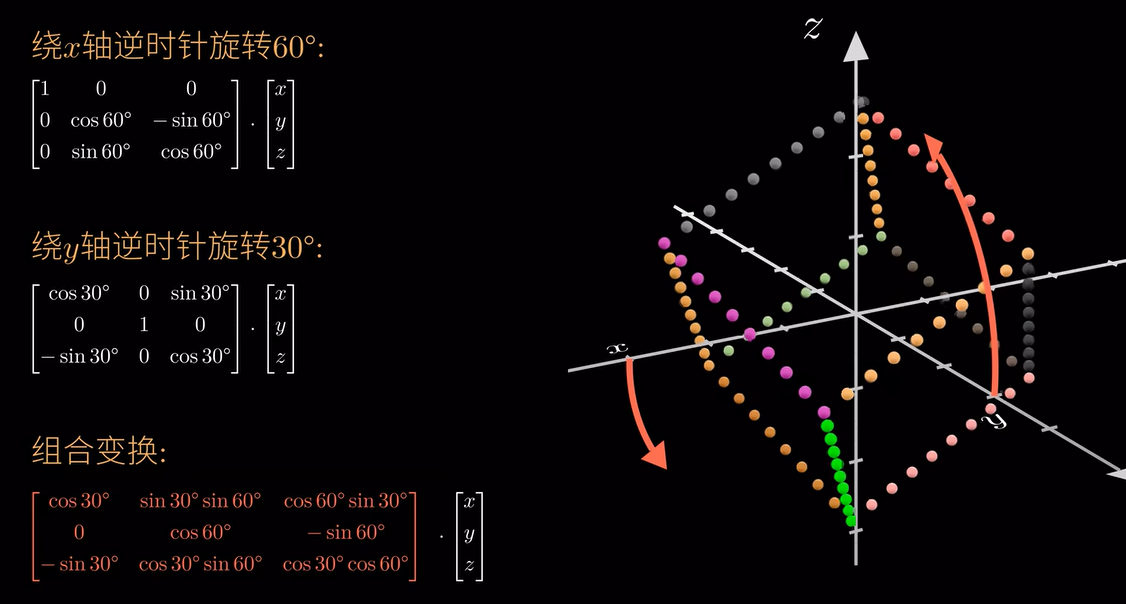
矩阵快速幂
计算斐波那契的第n项

将线性变换重复n次
思路
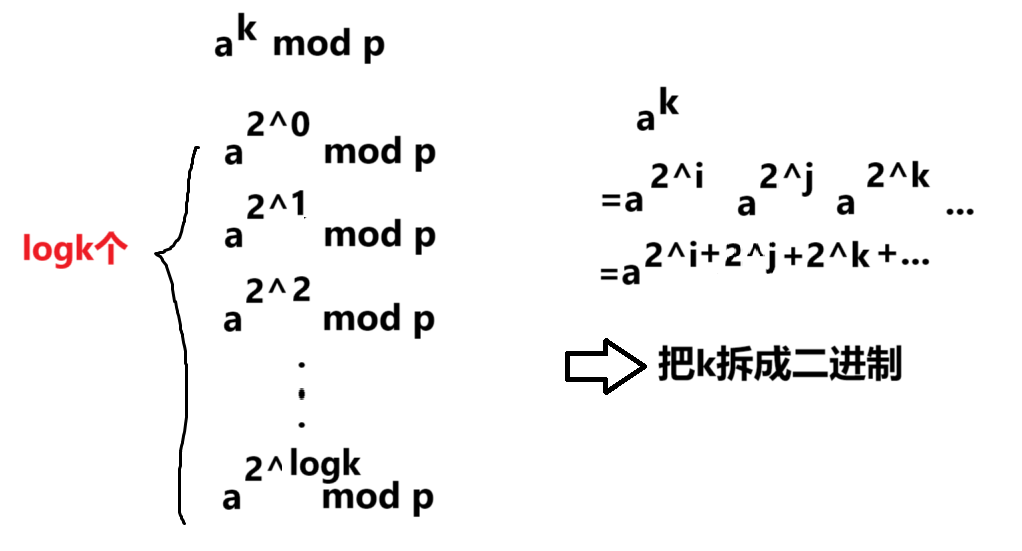
->k的二进制表示里,哪几位是1
举例
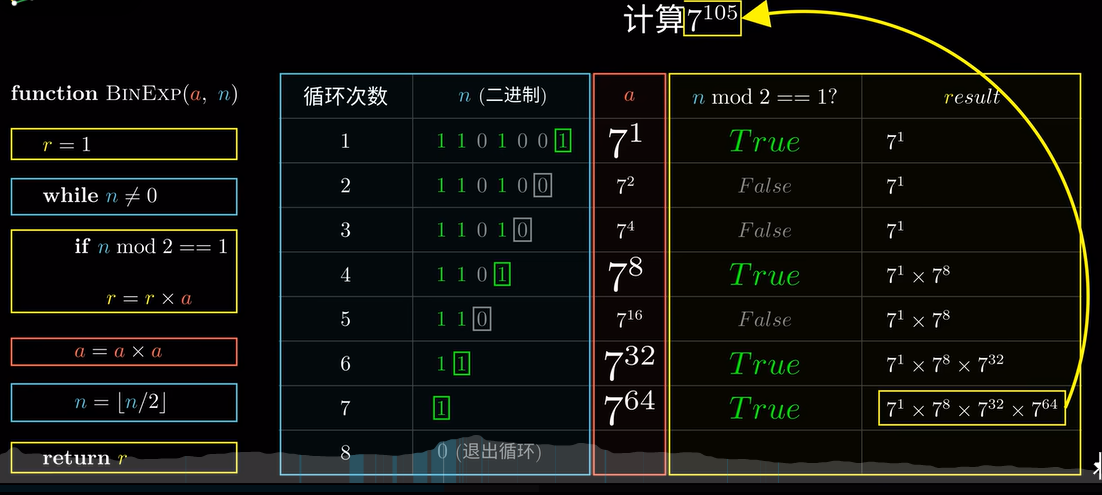
【快速幂模版】
ll qmi(ll a,ll k,ll p){
ll res=1;
while(k){
if(k&1) res=res*a%p;
k>>=1;//删去k的末位
a=a*a%p;
}
return res;
}
【矩阵快速幂】
constexpr int mod = 1000000007;
struct Matrix {
int a[3][3];
Matrix() { memset(a, 0, sizeof a); }
Matrix operator*(const Matrix &b) const {
Matrix res;
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 2; ++j)
for (int k = 1; k <= 2; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
} ans, base;
void init() {
base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;
ans.a[1][1] = ans.a[1][2] = 1;
}
void qpow(int b) {
while (b) {
if (b & 1) ans = ans * base;
base = base * base;
b >>= 1;
}
}
int main() {
int n = read();
if (n <= 2) return puts("1"), 0;
init();
qpow(n - 2);
println(ans.a[1][1] % mod);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号