【因数】（理论知识）

【因数】（理论知识）

求约数：试除法

时间复杂度 O(sqrt(n))

思路

约数是成对出现的->只枚举小的一个

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t;
int a;
vector<int> get_divisors(int n){
	vector<int> res;
	for(int i=1;i<=n/i;i++){
		if(n%i==0){
			res.push_back(i);
			//注意这里要判断 如果两个相同就只加一个 
			if(i!=n/i) res.push_back(n/i);
		}
	}
	sort(res.begin(),res.end());
	return res;
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      while(t--){
      	cin>>a;
      	vector<int> ans=get_divisors(a);
      	for(auto tt : ans) cout<<tt<<" ";
      	cout<<"\n";
	}
      return 0;
}

约数个数

思路

基于算术基本定理：每个数的因式分解结果是唯一的
每个数都有0~a[i]种选法->乘法定理

所有int范围内的整数 约数个数最多1500左右
https://www.acwing.com/problem/content/872/

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n; 
unordered_map<int,int> primes;//开哈希表存 
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>n;
      while(n--){
      	int x;
      	cin>>x;
      	//分解质因数 
      	for(int i=2;i<=x/i;i++){
      		while(x%i==0){
      			x/=i;
      			primes[i]++;
			}
		}
		//最后可能会剩一个较大质数 
		if(x>1) primes[x]++;
	}
	ll res=1;
	//unordered_map本质是pair的集合：可以用first和second 
	for(auto prime : primes) res=res*(prime.second+1)%mod;//公式 
	cout<<res<<"\n";
      return 0;
}

约数之和

思路

乘法分配律展开，每一项都是约数

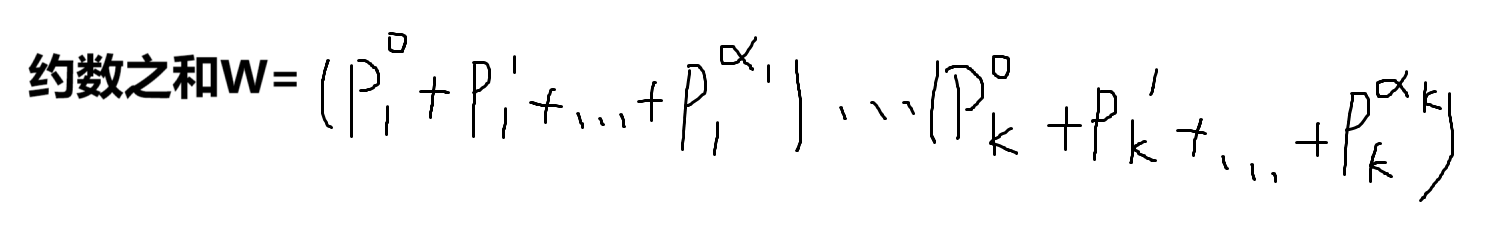
代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n; 
unordered_map<int,int> primes;
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>n;
      //先分解质因数 
      while(n--){
      	int x;
      	cin>>x;
      	for(int i=2;i<=x/i;i++){
      		while(x%i==0){
      			x/=i;
      			primes[i]++;
			}
		}
		//最后可能会剩一个较大质数 
		if(x>1) primes[x]++;
	}
	ll res=1;
	for(auto prime:primes){
		int p=prime.first,a=prime.second;//底数，指数
		//先求括号内的加
		ll t=1;
		//注意这里的求法 
		while(a--) t=(t*p+1)%mod;
		res=res*t%mod;
	}
	cout<<res<<"\n";
      return 0;
}

最大公约数：欧几里得算法/辗转相除法

时间复杂度 O(logn)

思路

代码

记得看数据范围（要不要用long long）

int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}

【题目整理】

小红走网格

https://ac.nowcoder.com/acm/contest/100253/C

思路

只要满足是gcd(x,y)的倍数->都可以达到

代码

//最大公约数：对于每个x gcd(a,b)的倍数都可以达到 
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
int t;
ll x,y,a,b,c,d;
ll gcd(ll a,ll b){
	return b?gcd(b,a%b):a;
}
void solve(){
	cin>>x>>y>>a>>b>>c>>d;
	ll numx=gcd(c,d);
	ll numy=gcd(a,b);
	if(x%numx==0 && y%numy==0) cout<<"YES"<<endl;
	else cout<<"NO"<<endl;
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      while(t--){
      	solve();
	}
      return 0;
}