【树状数组】

【树状数组】

模版代码

struct FenwickTree {
      vector<int> tree;
      int size;
      FenwickTree(int n){
            size=n;
            tree.resize(n+1,0);
      }
      void update(int pos, int delta){
            for(;pos<=size;pos+=pos&-pos)
                  tree[pos]+=delta;
      }
      int query(int pos){
            int res=0;
            for(;pos>0;pos-=pos&-pos)
                  res+=tree[pos];
            return res;
      }
      int rangeQuery(int l, int r){
            return query(r)-query(l-1);
      }
};

做到什么操作

快速求前缀和 O(logn)
修改某一个数 O(logn)

基本原理/推理过程

基于二进制

(L,R] 长度一定是R的二进制表示的最后一位1所对应的次幂
->区间可改写为 C[R]=[R-lowbit(R)+1,R]->长度是lowbit(R)
->c[x]=a[x-lowbit(x)+1,x]

树形结构

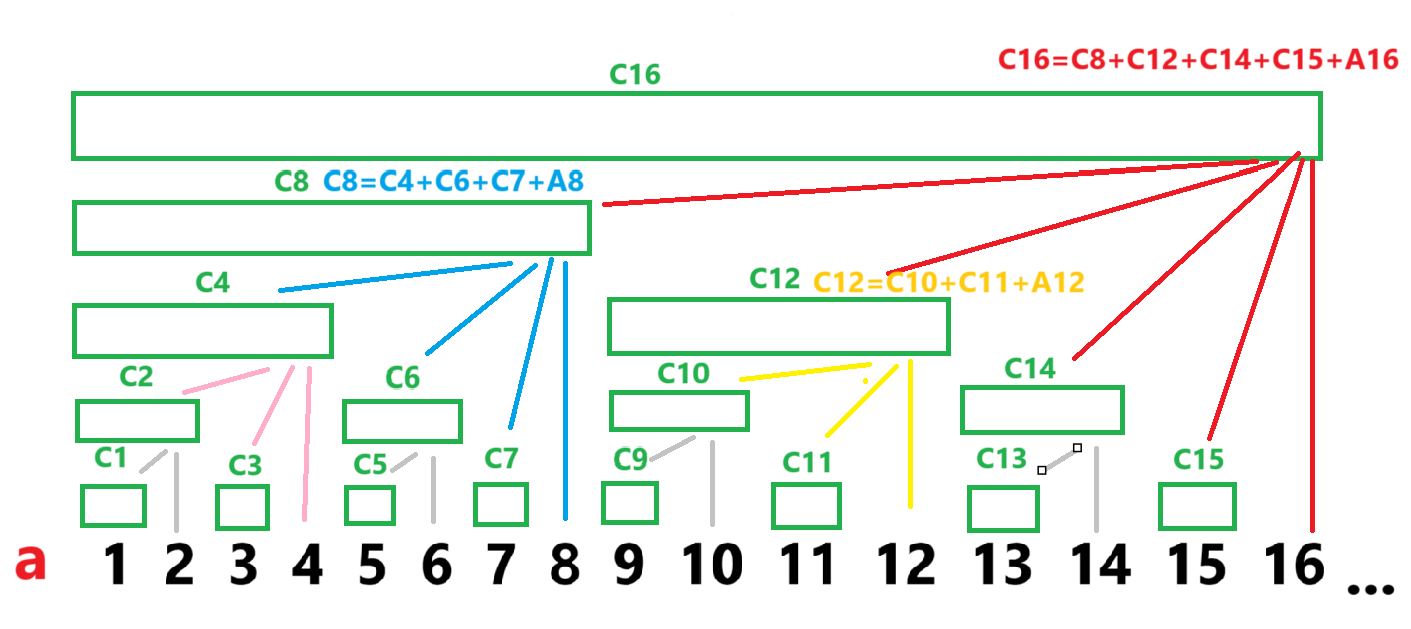
通过父节点找子节点：x->x-1->二进制表示下位若干个1->从低位往高位依次找1（每个1就是一个儿子）
->反推：通过子节点找父节点（修改操作）
每一个点被修改过后->直接影响的区间是唯一的
p=x+lowbit(x)
修改操作

若a[x]+=c:
for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;

查询操作

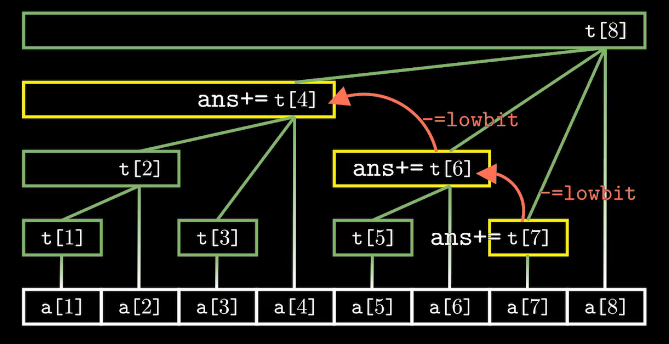
查询1-x的和
for(int i=x;i;i-=lowbit(i)) sum+=tr[i];
//tr[i]：起始点为i 长度为lowbit(i)的区间和

模版代码

lowbit：求非负整数x在二进制表示下最低位1及其后面的0构成的数值

int lowbit(int x)
{
    return x & -x;
}

修改

//序列中第x个数加上k
void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += k;
}

查询

//查询序列中第1~x的数的和
int ask(int x)
{
    int sum = 0;
    for(int i = x; i; i -= lowbit(i))
        sum += t[i];
    return sum;
}

初始化

//一般都是直接加 O(nlogn)
for(int i=1;i<=n;i++) add(i,a[i]);

例题

楼兰图腾

https://www.luogu.com.cn/problem/P10589

思路

以V型为例，A型同理


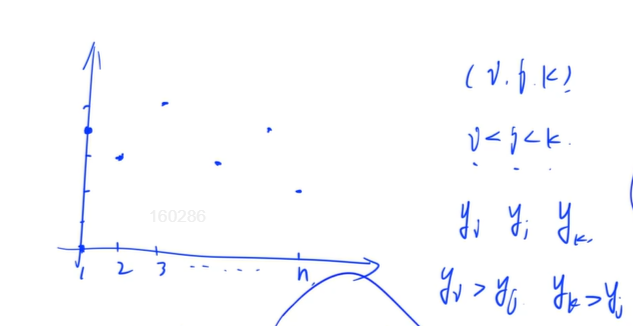
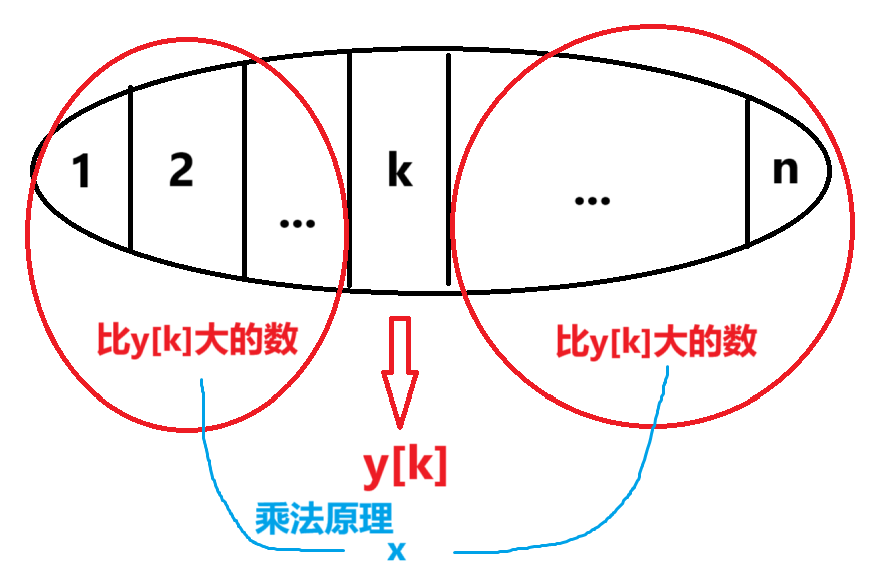
从左往右扫一遍 greater[k]：1~k+1有多少个数在y[k]+1~n之间
从右往左扫一遍 lower[k]：k+1~n有多少个数在y[k]+1~n之间
->树状数组统计区间和

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2000010;
int n,a[N];
int tr[N];
int Greater[N],Lower[N];//注意题目：y1-yn是1-n的一个排列 
//Lower[i]表示左边比第i个位置小的数的个数
//Greater[i]表示左边比第i个位置大的数的个数 （greater和lower都不能直接用） 
int lowbit(int x){
	return x&-x;
}
void add(int x,int c){
	for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
//求前缀和 
int ask(int x){
	int res=0;
	for(int i=x;i;i-=lowbit(i)) res+=tr[i];
	return res;
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>n;
      for(int i=1;i<=n;i++) cin>>a[i];
      //从左向右依次更新greater和lower
	//注意：树状数组存的是数的出现次数！（桶） 
      for(int i=1;i<=n;i++){
      	int y=a[i];
      	//在前面已加入树状数组的所有数中统计在区间[y + 1, n]的数字的出现次数
      	Greater[i]=ask(n)-ask(y);
      	//在前面已加入树状数组的所有数中统计在区间[1, y - 1]的数字的出现次数
      	Lower[i]=ask(y-1);
      	//将y加入树状数组，即数字y出现1次
      	add(y,1);
	}
	//清空树状数组->从右往左统计每个位置右边比第i个数y小的数的个数、以及大的数的个数
      memset(tr, 0, sizeof tr);
      //注意开longlong 
      ll resV=0,resA=0;
      for(int i=n;i>=1;i--){
      	int y=a[i];
      	resV+=(ll)Greater[i]*(ask(n)-ask(y));
      	resA+=(ll)Lower[i]*(ask(y-1));
      	add(y,1);
	}
	cout<<resV<<" "<<resA;
      return 0;
}

扩展

差分

例题 https://www.acwing.com/file_system/file/content/whole/index/content/3797/

【题目积累】

一般利用树状数组来将循环算法的\(n\)优化为\(logn\)

小苯的极大支配

https://ac.nowcoder.com/acm/contest/122724/F

题意

思路

显然枚举这个极大值
（1）对于比极大值还要大的值：要全部删去->前缀和维护即可
（2）对于比极小值要小的值：要削到比p[max]小
->若暴力：

for(int j=1;j<=i-1;j++){
    if(p[j]>=p[i]) res+=p[j]-p[i]+1;
}

->对于p[j]-p[i]+1->想以求和的方式计算->树状数组维护
->从前往后加入，树状数组下标为出现次数p[i]，开两个树状数组分别维护p[j]总和、个数
->有每次枚举：p[j]总和-个数*p[i]+个数

代码

void solve(){
    cin>>n;
    vector<int> a(n+1,0);
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    vector<int> p(n+1,0),s(n+1,0);
    for(int i=1;i<=n;i++) p[a[i]]++;
    s[n]=p[n];
    for(int i=n-1;i>=1;i--){
        s[i]=s[i+1]+p[i];
    }
    FenwickTree ft1(n),ft2(n);//下标为出现次数
    int ans=1e9;
    for(int i=1;i<=n;i++){
        if(p[i]>0){
            int res=s[i+1];
            int tmp1=ft1.rangeQuery(p[i],n);
            int tmp2=ft2.rangeQuery(p[i],n);
            int tmp3=tmp1-tmp2*p[i]+tmp2;
            res+=tmp3;
            ans=min(ans,res);
            ft2.update(p[i],1);
            ft1.update(p[i],p[i]);
        }
    }
    cout<<ans<<endl;
}