【树形DP】
【树形DP】
参考:https://www.cnblogs.com/hanruyun/p/9788170.html
总结
典型例题
烷烃计数
https://atcoder.jp/contests/abc394/tasks/abc394_f
/*【树形DP】
状态表示:dp[u][j]:以u为中心节点 选择j条分支所能得到的最大子树
状态转移:只能选择1或者4个分支->不需要统计度数 每个节点的贡献值为1
不添加分支(0)+添加3个分支(3)
*/
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
const int INF=-0x3f3f3f3f;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=1e6+10;
int n;
int h[N],ne[N],e[N],idx;
int dp[N][5];
int ans=INF;
void add(int x,int y){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int u,int fa){
dp[u][0]=1;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(j!=fa){
//先递归找子节点
dfs(j,u);
for(int k=4;k>=1;k--){//必须要从4开始一路迭代下去->才能一直更新:选择j个分支的情况是由选择j-1个分支扩展的
//要么加3个分支,要么一个分支都不加
dp[u][k]=max(dp[u][k],dp[u][k-1]+max(dp[j][3],dp[j][0]));
}
}
}
ans=max(ans,dp[u][1]);
ans=max(ans,dp[u][4]);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
memset(h,-1,sizeof h);
//初始化dp最小
for(int i=0;i<=n;i++){
for(int j=0;j<=4;j++) dp[i][j]=INF;
}
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
add(u,v);add(v,u);
}
dfs(1,-1);
if(ans>4) cout<<ans;
else cout<<"-1";
return 0;
}
非典型例题
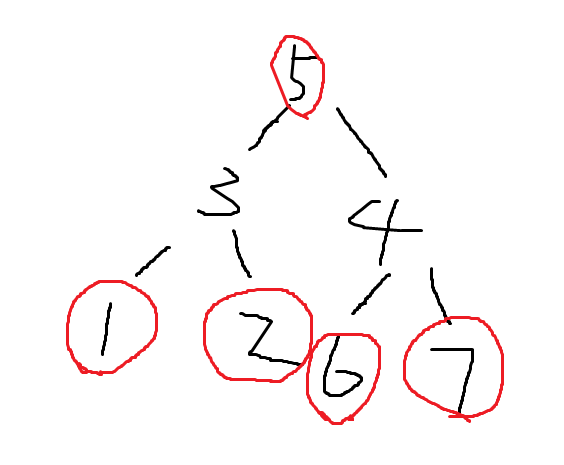
没有上司的舞会
https://fjnuacm.top/d/minor/p/286?tid=66cdb20d71a91e475b1e6ac7
这样选最多
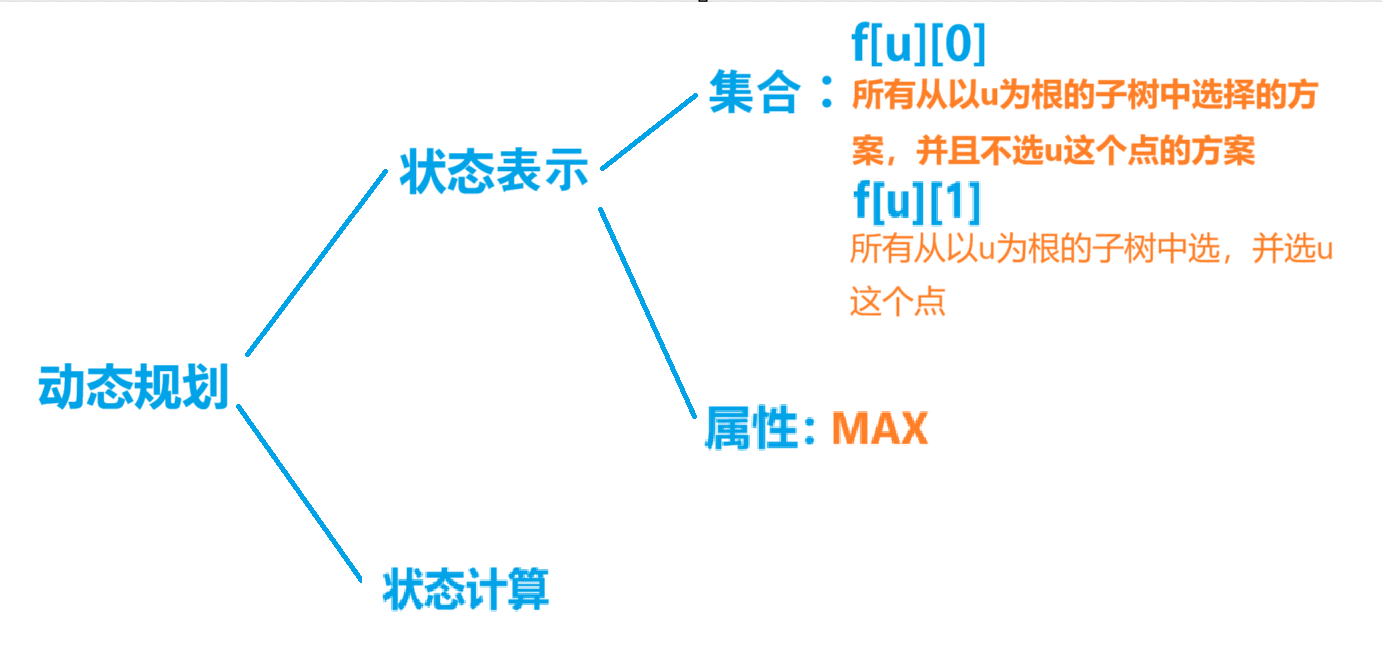
【DP分析】
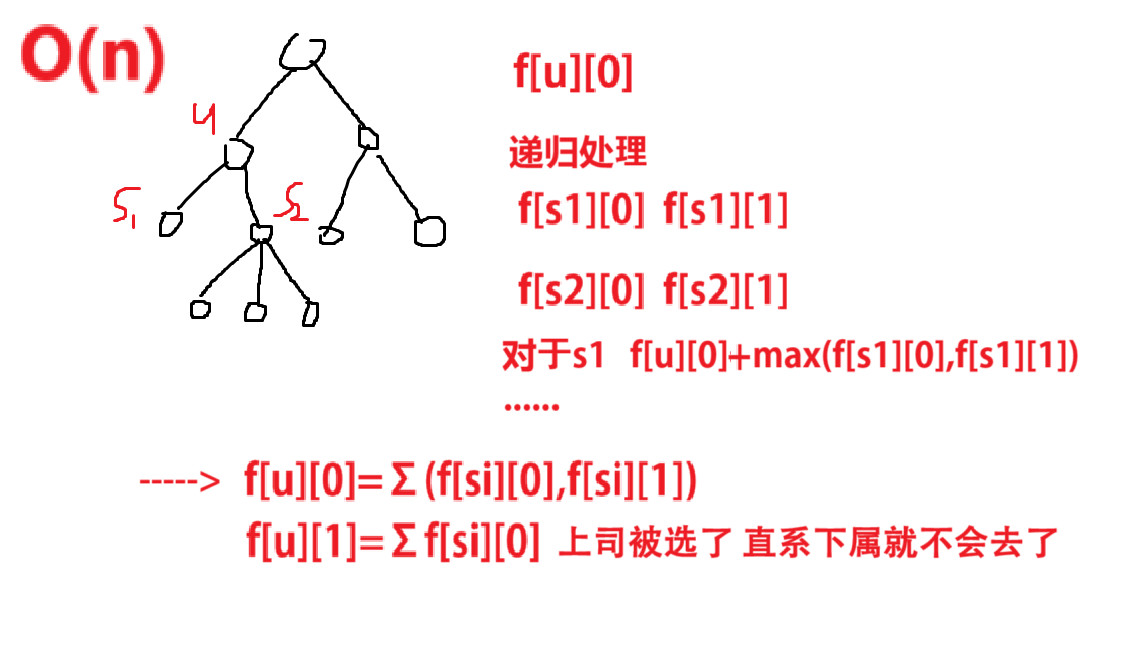
代码
#include<bits/stdc++.h>
using namespace std;
const int N=6010;
int n;
int happy[N];
int h[N],e[N],ne[N],idx;
int f[N][2];//第二维:0不选 1选
//题目没有告诉我们父节点:要自己找
bool has_father[N];
void add(int x,int y){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int u){
f[u][1]=happy[u];//选的话要把该点happy值加上
//递归找子树
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
dfs(j);
//若不选这个点:在子树的选与不选中取最大值在+
f[u][0]+=max(f[j][1],f[j][0]);
//若选这个点:子树不能选
f[u][1]+=f[j][0];
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&happy[i]);
memset(h,-1,sizeof h);//邻接表一定要初始化!
for(int i=0;i<n-1;i++){
int a,b;
scanf("%d%d",&a,&b);
has_father[a]=true;
add(b,a);
}
//找根:没有父节点的
int root=1;
while(has_father[root]) root++;
dfs(root);
int ans=max(f[root][0],f[root][1]);
printf("%d",ans);
return 0;
}
二叉苹果树
https://fjnuacm.top/d/minor/p/287?tid=66cdb20d71a91e475b1e6ac7
【树形dp一般套路】
(1)dp[u][i][j]... :
当前节点为u
前i个节点
j... 表示其他状态:重量?
(2)一般要枚举第二维节点状态:for(int k=0;k<=j;k++)...
(3)dp式内(一般是dfs有返回值时)/提前递归处理子树
思路+代码
/*【树形dp】
【状态表示】
dp[i][j]表示为,当前结点为i,保留树枝条数为j的情况下,所留下苹果数的最大值
【特殊情况】
(1)ls[i]==0 && rs[i]==0 -->叶节点-->返回0
(2)j==0 保留树枝条数为0
【状态转移】
设中间量k:枚举,给左儿子分配的树枝数k,给右儿子分配的即为 j-k
一般式:
dp[i][j]=max(dp[ls[i]][k-1]+dp[rs[i]][j-k-1]+la[i]+ra[i])
最左/最右单独处理
k=0 没有左边 dp[rs[i]][j-1]+ra[i]
k=j 没有右边 dp[ls[i]][j-1]+la[i]
-->递归完成
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1100;//注意这里:要开邻接表且双向存图->空间会更大
int n,q;
/*
ls rs左右儿子
la ra 左右儿子边上的苹果
*/
int ls[N],rs[N],la[N],ra[N];
int val[N],h[N],e[N],ne[N],idx;
int dp[N][N];
//邻接表-->注意val值也被idx表示!-->双链表存值不会乱(一个点可能有两个值)
void add(int x,int y,int v){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx;
val[idx++]=v;
}
//※将邻接表转换为树
void tree(int x,int fa){//当前值和父节点值
int g=0;//计数器,分配左右儿子
for(int i=h[x];i!=-1;i=ne[i]){
int y=e[i];
if(y!=fa){//在单链表中,不是父节点就是儿子节点
g++;
if(g==1){//分配左儿子
ls[x]=y;
la[x]=val[i];//注意val下标是idx的计数!
}
else{
rs[x]=y;
ra[x]=val[i];
}
tree(y,x);//递归建树
}
}
}
int dfs(int i,int j){ //dp[i][j]以i为根,保留j个树枝的最大值
//特殊情况
if(ls[i]==0 && rs[i]==0) return 0;
if(j==0) return 0;
if(dp[i][j]>0) return dp[i][j];//※一个优化剪枝:这个点已经被更新过了就直接返回
//dp递归写法!
for(int k=0;k<=j;k++){
//不走左边 走右边
if(k==0) dp[i][j]=max(dp[i][j],dfs(rs[i],j-1)+ra[i]);
//不走右边 走左边 -->注意else
else if(k==j) dp[i][j]=max(dp[i][j],dfs(ls[i],j-1)+la[i]);
//一般情况:给左边分k个 右边就是j-k个
//由于走到儿子结点都需要经过一条树枝,所以实际上分配数都要-1
else dp[i][j]=max(dp[i][j],dfs(ls[i],k-1)+la[i]+dfs(rs[i],j-k-1)+ra[i]);
}
return dp[i][j];
}
int main(){
scanf("%d%d",&n,&q);
memset(h,-1,sizeof h);
for(int i=1;i<n;i++){
int aa,bb,qq;
scanf("%d%d%d",&aa,&bb,&qq);
//无向图:建双边
add(aa,bb,qq);
add(bb,aa,qq);
}
//建树
tree(1,0);
int ans=dfs(1,q);
printf("%d",ans);
return 0;
}
选课
https://fjnuacm.top/d/minor/p/288?tid=66cdb20d71a91e475b1e6ac7
※注意本题提前递归子树
【代码】
/*
【状态表示】
dp[u][i]表示以节点u为根的子树,选择i个点可以获得的最大权值和
-->发现每个子节点都会占用父节点i的一部分,又有一个贡献,可以选择或不选择
-->01背包
-->dp[u][i][j]表示节点u的前i个子节点,限重为j能得到的最大权值和
-->优化:dp[u][j]表示节点u,限重j的最大权值和
-->dp[i][1]表示该节点本身权值(只能选自己) --> 递推起点dp[now][1][1]=val[now]
【状态转移】
dp[u][i][j]=max(dp[now][i-1][j],dp[son][所有节点数][k]+dp[now][i-1][j-k]);
-->我要用到i-1的内容 都是满足k<j的 -->所以倒着循环j -->01背包优化
for(int i=head[u]; i; i=e[i].next)//遍历所有子节点
for(int j=n, v=e[i].to; j>0; --j)//这里和01背包一样,总重从大到小循环
for(int k=0; k<j; ++k)//这里是不同之处,子节点的重量需要规定
dp[u][j]=max(dp[u][j], dp[u][j-k]+dp[v][k]); dp[v][k]=dp[son][所有节点数][k] 递归处理儿子
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int h[N],ne[N],e[N],idx;
int n,m;
int dp[N][N];
void add(int x,int y){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int u){
//递归先处理子节点
for(int i=h[u];i!=-1;i=ne[i]) dfs(e[i]);
for(int i=h[u];i!=-1;i=ne[i]){
int y=e[i];
for(int j=n;j>0;j--){//01背包优化:总重从大到小循环
for(int k=0;k<j;k++){//根节点一定要被选:dp[u][j-k]一定要留1
dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[y][k]);
}
}
}
}
int main(){
scanf("%d%d",&m,&n);
n++;//原题为森林,要加0(根节点)-->必须被选
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int aa;
//会有一个空节点0,如果是不需要先修课的就加到头节点下面去
scanf("%d%d",&aa,&dp[i][1]);//不用专门存val
add(aa,i);
}
dfs(0);
printf("%d",dp[0][n]);
return 0;
}
加分二叉树
https://www.luogu.com.cn/problem/P1040
※树形dp写法+二叉树特性
/*【思路】
中序遍历:每一个节点都有可能成为根
计算规则:左子树x右子树+根节点->递归定义
->有重复状态
【区间DP】
dp[i][j] -> 节点i到j成树的最大得分 -> 答案即为dp[1][n]
->区间内枚举根即可
初始化:dp[i][i]=a[i]
->注意左右子树为空的情况(一定不是最优解)
根据中序遍历性质:dp[i][k-1]左子树 dp[i][k+1]右子树
【输出前序遍历】
root[i][j] -> 记录i-j成树时的根节点 -> 递归输出
*/
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int n,a[N];//注意a是存值!
long long f[N][N];//注意开longlong
int root[N][N];
//递归输出前序遍历(输出节点编号):根->左->右
void print(int l,int r){
if(l>r) return;//递归出口
//输出根节点
printf("%d ",root[l][r]);
if(l==r) return;//该树只有一个节点->退出
//找左子树
print(l,root[l][r]-1);
//找右子树
print(root[l][r]+1,r);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
//初始化dp和root
f[i][i]=a[i];
f[i][i-1]=1;
f[i+1][i]=1;
root[i][i]=i;//自己是自己树的根节点
}
for(int len=1;len<=n;len++){
for(int i=1;i+len<=n;i++){
int j=i+len;//要讨论左右子树为空->可初始化左子树空 右子树空在找的时候体现->长度要溢出一格
f[i][j]=f[i+1][j]+f[i][i];//左右子树为空时->一定不是最优解
root[i][j]=i;//默认从起点选根
for(int k=i;k<=j;k++){//会出现下标反的情况->约定为1(看上面初始化)
int res=f[i][k-1]*f[k+1][j]+f[k][k];
if(f[i][j]<res){
f[i][j]=res;
root[i][j]=k;
}
}
}
}
printf("%lld\n",f[1][n]);
print(1,n);
return 0;
}
皇宫看守
https://www.acwing.com/file_system/file/content/whole/index/content/4184022/
【解法一】树形DP
※状态设计
//要开longlong!
/*【解法2:树形dp】
线性dp->转2维->【状态设计】->要拓展不放守卫的情况:父亲,儿子
dp最小值
dp[i][1]:当前点放守卫
dp[i][2]:当前点不放守卫->被子节点监视->找最小儿子
dp[i][3]:当前点不放守卫->被父节点监视->子节点的子节点要放
*/
#include<bits/stdc++.h>
using namespace std;
const int N=15000;
typedef long long ll;
int n;
ll k[N];
int e[N],h[N],ne[N],idx;
ll dp[N][5];
bool has_father[N];
void add(int x,int y){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int u){
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
dfs(j);//先递归找子树->从下向上找
//情况1
dp[u][1]+=min(dp[j][1],min(dp[j][2],dp[j][3]));
//情况3:儿子的儿子一定要有
dp[u][3]+=dp[j][2];
}
//选自己要加上自己
dp[u][1]+=k[u];
//处理情况2:找自己最小的儿子->其他儿子保持原样->无所谓
int sum=0;//先记录处理前的所有子节点的状态
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
sum+=min(dp[j][1],dp[j][2]);//记录最小值
}
//初始化一个最大值
dp[u][2]=2147483640;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];//j点放守卫->去掉j点原先状态,并加上放守卫的状态(其他点无关)
dp[u][2]=min(dp[u][2],sum-min(dp[j][1],dp[j][2])+dp[j][1]);
}
}
int main(){
scanf("%d",&n);
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++){
int tmp;
scanf("%d",&tmp);
scanf("%lld",&k[tmp]);
int m;
scanf("%d",&m);
while(m--){
int son;
scanf("%d",&son);
add(tmp,son);//默认往下找
has_father[son]=1;
}
}
//找根
int root=1;
while(has_father[root]) root++;
dfs(root);
ll ans=min(dp[root][1],dp[root][2]);
printf("%lld",ans);
return 0;
}
叶子的染色
https://fjnuacm.top/d/minor/p/292?tid=66cdb20d71a91e475b1e6ac7
思路
【状态表示】f[i][j] 第i个点 将其染成j颜色 所耗费的次数
【状态转移】
如果某一点需要染成x色,且它的父节点已经被染成x色->它不需要被染色
->(1)直接继承父亲对应颜色的次数
(2)保持父亲为非x色,并单独将此节点染成x色
->状态转移方程:
u是v的父亲节点
f[u][0]+=min(f[v][0]-1,f[v][1])
f[u][1]+=min(f[v][1]-1,f[v][0])
->将一个节点 染成颜色j的代价,即为其所有子节点染成颜色j代价的和

代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10010,M=300010;
const int INF=2147483647;
int m,n;
int c[N];
int h[N],ne[M],e[M],idx;
int f[N][3];
int root=-1;
void add(int x,int y){
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int u,int fa){
if(u<=n) return;//叶节点直接跳过
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(j!=fa){//跳过父节点
dfs(j,u);//从下而上->递归找子树
f[u][0]+=min(f[j][0]-1,f[j][1]);
f[u][1]+=min(f[j][1]-1,f[j][0]);
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>m>>n;//n以内的点都是儿子
for(int i=1;i<=n;i++) cin>>c[i];
memset(h,-1,sizeof h);
for(int i=1;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
root=n+1;//随便找一个点当根
//初始化
for(int i=1;i<=m;i++){
f[i][0]=f[i][1]=1;
if(i<=n) f[i][!c[i]]=INF;//叶节点:表示不应染成该色
}
dfs(root,root);
int ans=min(f[root][0],f[root][1]);
cout<<ans;
return 0;
}
三色二叉树
https://fjnuacm.top/d/minor/p/293?tid=66cdb20d71a91e475b1e6ac7
注意二叉树存树方式:邻接矩阵
注意没有dfs而是用递推(二叉树性质)
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=500010;
string s;
int n;
//二叉树存节点:邻接矩阵
int tree[N][2],idx;
//tr[i][0]表示i的左儿子
//tr[i][1]表示i的右儿子
int dp[N][3];//0染绿色 1不染绿色
int ansmax=-1,ansmin=0x3f3f3f3f;
void tr(int x){
idx++;//idx表示访问过多少个节点(从1开始计数)
if(s[x]=='0') return;//叶节点直接return
if(s[x]=='1'){
tree[x][0]=x+1;//下一个访问的节点的编号一定是这个节点编号+1
tr(x+1);
}
if(s[x]=='2'){
tree[x][0]=x+1;
tr(x+1);
//注意右子树建树过程!
tree[x][1]=idx+1;//右节点一定是总共访问的编号+1
tr(idx+1);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>s;
n=s.size();
s=' '+s;
tr(1);
//递推dp:直接从后往前(叶节点开始)即可
for(int i=n;i>=1;i--){//若i遍历到了叶节点:默认左右子树为0->可初始化染色时方案数为1
dp[i][0]=dp[tree[i][0]][1]+dp[tree[i][1]][1]+1;//若染色:两个子树不染色+1
dp[i][1]=max(dp[tree[i][0]][0]+dp[tree[i][1]][1],dp[tree[i][1]][0]+dp[tree[i][0]][1]);
}
ansmax=max(dp[1][0],dp[1][1]);
memset(dp,0,sizeof dp);
for(int i=n;i>=1;i--){
dp[i][0]=dp[tree[i][0]][1]+dp[tree[i][1]][1]+1;
dp[i][1]=min(dp[tree[i][0]][0]+dp[tree[i][1]][1],dp[tree[i][1]][0]+dp[tree[i][0]][1]);
}
ansmin=min(dp[1][0],dp[1][1]);
cout<<ansmax<<" "<<ansmin;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号