【拓扑排序/图的BFS】

【拓扑排序/图的BFS】

有向图

重边

自环

图的BFS

【思路】

queue<-1
while(queue不空){
	t<-队头
	拓展t所有邻边x
	if（x未遍历）{
		queue<-x
		d[x]=d[t]+1
	}
}

例题:图中点的层次

https://www.acwing.com/problem/content/849/

【代码】

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m; 
//邻接表 
int h[N],e[N],ne[N];
int idx;
//d存距离，q队列bfs 
int d[N],q[N];
void add(int x,int y){
	e[idx]=y;
	ne[idx]=h[x];
	h[x]=idx++;
}
int bfs(){
	int hh=0,tt=0;
	q[hh]=1;
	memset(d,-1,sizeof d);//如果无法到达->输出-1 
	d[1]=0;
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];i!=-1;i=ne[i]){
			int j=e[i];
			if(d[j]==-1){
				d[j]=d[t]+1;
				q[++tt]=j;
			}
		}
	}
	return d[n];
}
int main(){
	scanf("%d%d",&n,&m);
	memset(h,-1,sizeof h);
	for(int i=0;i<m;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	printf("%d",bfs());
	return 0;
}

拓扑序

※图的BFS的应用

性质

（1）只有有向图才有拓扑序
（2）环没有拓扑序
（3）有向无环图一定存在拓扑序列：拓扑图

eg 拓扑序 1 2 3

（4）度数

入度：有多少条边指向自己
出度：它指向多少条边

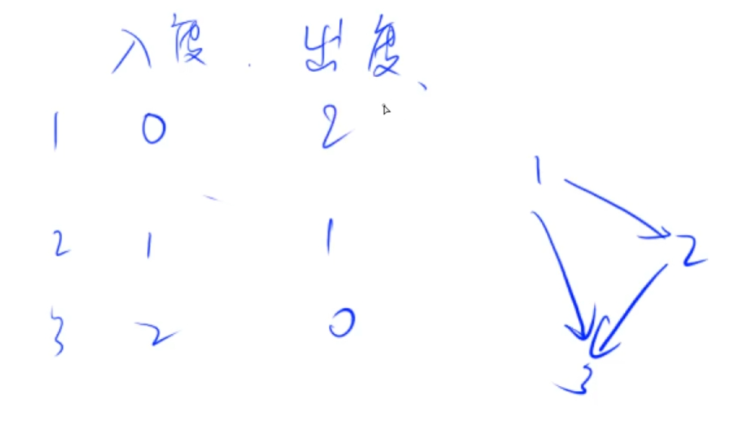
入度为0：没有任何点指向它->适合当首项
一个有向无环图，至少存在一个入度为0的点

求拓扑序

【伪代码】

queue<-所有入度为0的点
while(queue不空){
	t<-队头
	枚举t的所有出边 t->j
		删掉t->j,d[j]--
		if(d[j]==0)
			queue<-j
}

拓扑序：队列的次序

例题

https://www.acwing.com/problem/content/850/

【代码】

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],ne[N],e[N],idx;
int q[N],d[N];//d存入度 
void add(int x,int y){
	e[idx]=y;
	ne[idx]=h[x];
	h[x]=idx++;
}
bool topsort(){
	int hh=0,tt=-1;
	for(int i=1;i<=n;i++){//题目中 点从1开始
		if(!d[i]) q[++tt]=i;
	}
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];i!=-1;i=ne[i]){
			int j=e[i];
			d[j]--;//入度-1（删掉边）
			if(d[j]==0) q[++tt]=j;//入度为0：入队 
		}
	}
	return tt==n-1;
}
int main(){
	scanf("%d%d",&n,&m);
	memset(h,-1,sizeof h);//一定不要忘记h初始化-1！！！
	for(int i=0;i<m;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b); 
		d[b]++;//更新入度 
	}
	if(topsort()){//队列顺序就是拓扑序 
		for(int i=0;i<n;i++) printf("%d ",q[i]);
		puts("");
	}
	else puts("-1");
	return 0;
}

拓扑序求法应用+记忆化搜索：食物链

https://www.luogu.com.cn/problem/P3183

思路

拓扑序+统计每个点的方案数，并进行累加
注意bfs时先排除单个点（入度为0 出度为0） 再进行bfs
答案为所有入度为0且出度不为0的点（结尾）的方案数总和

代码

//拓扑排序+f统计方案 -> 答案为无出度的点的方案数总和 
//入度为0的点为起点 出度为0的点为终点 
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int h[N],e[N],ne[N],idx;
int n,m;
int r[N],c[N];//入度，出度 
int f[N];//记忆化统计方案 
int q[N];
int ans;
void add(int x,int y){
	e[idx]=y;
	ne[idx]=h[x];
	h[x]=idx++;
}
//拓扑排序 
void bfs(){
	int hh=0,tt=-1;
	//搜索每一个入度为0且出度不为0的点->排除单个点 
	for(int i=1;i<=n;i++){
		if(!r[i] && c[i]){
			q[++tt]=i;
			f[i]=1;
		}
	}
	while(hh<=tt){
		int t=q[hh++];
		if(!r[t] && !c[t]) ans+=f[t];//统计答案->前面已经把单个点排除了->这里不用考虑 
		//所有和它相连的点 
		for(int i=h[t];i!=-1;i=ne[i]){
			int j=e[i];
			f[j]+=f[t];//往下走：方案数累加 
			r[j]--;//入度-1 
			if(!r[j]) q[++tt]=j;//当入度为0时加入队列 
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	memset(h,-1,sizeof h);
	for(int i=0;i<m;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
		r[b]++;
		c[a]++;
	}
	bfs();
	printf("%d",ans);
	return 0;
}