【图的存储】

【图的存储】

邻接表/邻接矩阵

※用来存有向图
无向图：一种特殊的有向图->存两次

add(a,b);
add(b,a);

代码实现：链式前向星

头插法

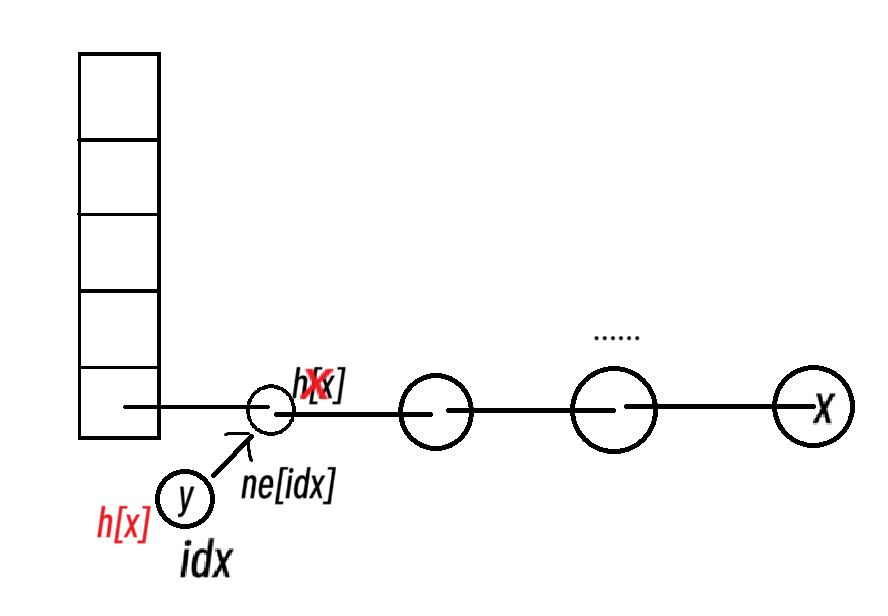
【插入】

int idx=0; //节点序号
int h[M];//头结点：记得初始化为-1！
int e[M];//存储该节点的值 
int ne[M];//存储该节点的下一个点的位置

//x所对应的单链表中插入y x为根结点 
void add(int x,int y){
    e[idx]=y;
    ne[idx]=h[x];
    h[x]=idx++;
}

【遍历】

for(int i=h[u];i!=-1;i=ne[i]){
    int j=e[i]; 
    if(!st[j]){
        
    }
}

如果题目只和边有关系：不一定非得要链式前向星

直接vector<int> g[N]存即可

[例题]Remove Exactly Two

https://codeforces.com/contest/2063/problem/C

#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
vector<int> g[N];//直接使用存儿子的邻接表即可！ 
int deg[N];
void solve() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        g[i].clear();
        deg[i] = 0;
    }
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--; v--;  // 为了方便从0开始编号
        g[u].push_back(v);
        g[v].push_back(u);
        deg[u]++;
        deg[v]++;
    }
    int ans = 0;
    multiset<int> s;
    for (int j = 0; j < n; j++) {
            s.insert(deg[j]);
        }
    for (int i = 0; i < n; i++) {
        s.erase(s.find(deg[i]));
        s.insert(0);
        for (int j : g[i]) {
            s.erase(s.find(deg[j]));
            s.insert(deg[j] - 1);
        }
        int maxDeg = *s.rbegin();
        ans = max(ans, deg[i] + maxDeg - 1);
        s.erase(s.find(0));
        s.insert(deg[i]);
        for (int j : g[i]) {
            s.erase(s.find(deg[j]-1));
            s.insert(deg[j]);
        }
    }
    cout << ans << endl;
}
int main() {
	ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[例题]树的重心

https://www.acwing.com/problem/content/848/
【样例】

【dfs过程】

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=N*2;//存无向图：节点数要*2
int n;
//邻接表存储图 
int h[M];//头结点 
int e[M];//存储该节点的值->原先的编号
int ne[M];//存储该节点的下一个点的位置
int idx=0; 

bool st[M];//标记这个点有没有被走过：dfs每个点只会走1次 
int ans=N; 

//x所对应的单链表中插入y x为根结点 
void add(int x,int y){
    e[idx]=y;
    ne[idx]=h[x];
    h[x]=idx++;
}
int dfs(int u){
    int res=0;//删掉某个节点后，最大的连通块节点数 
    st[u]=true;//标记这个点被走过 
    int sum=1;//以u为根节点的树的节点数->包括u所以初始化为1
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];//这里的值->树原先的编号
        if(!st[j]){
            int s=dfs(j);//递归找子树 
            res=max(res,s);
            sum+=s;//以j为根的树 的节点数 
        }
    }
    //父节点所连通块的节点数：n-sum 
    res=max(res,n-sum);
    ans=min(ans,res);
    return sum;//递归找子树需要返回的节点值 
}
int main(){
    scanf("%d",&n);
    memset(h,-1,sizeof h);//头结点初始化为-1
    //不用初始化ne：在插入的过程中就可以自动变为-1了 
    for(int i=0;i<n-1;i++){//【无环图】n-1行数据：n个节点 n-1条边 
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);//无向图是一种特殊的有向图->插入两次 
    }
    dfs(1);
    printf("%d",ans);
    return 0;
}