【并查集】
并查集
解决连通性问题
模版代码
带启发式合并
struct DSU {
vector<int> fa, p, e, f;
DSU(int n) {
fa.resize(n + 1);
iota(fa.begin(), fa.end(), 0);
p.resize(n + 1, 1);
e.resize(n + 1);
f.resize(n + 1);
}
int get(int x) {
while (x != fa[x]) {
x = fa[x] = fa[fa[x]];
}
return x;
}
bool merge(int x, int y) { // 设x是y的祖先
if (x == y) f[get(x)] = 1;
x = get(x), y = get(y);
e[x]++;
if (x == y) return false;
if (x < y) swap(x, y); // 将编号小的合并到大的上
fa[y] = x;
f[x] |= f[y], p[x] += p[y], e[x] += e[y];
return true;
}
bool same(int x, int y) {
return get(x) == get(y);
}
bool F(int x) { // 判断连通块内是否存在自环
return f[get(x)];
}
int size(int x) { // 输出连通块中点的数量
return p[get(x)];
}
int E(int x) { // 输出连通块中边的数量
return e[get(x)];
}
};
1.将两个集合合并
2.询问两个元素是否在同一集合中
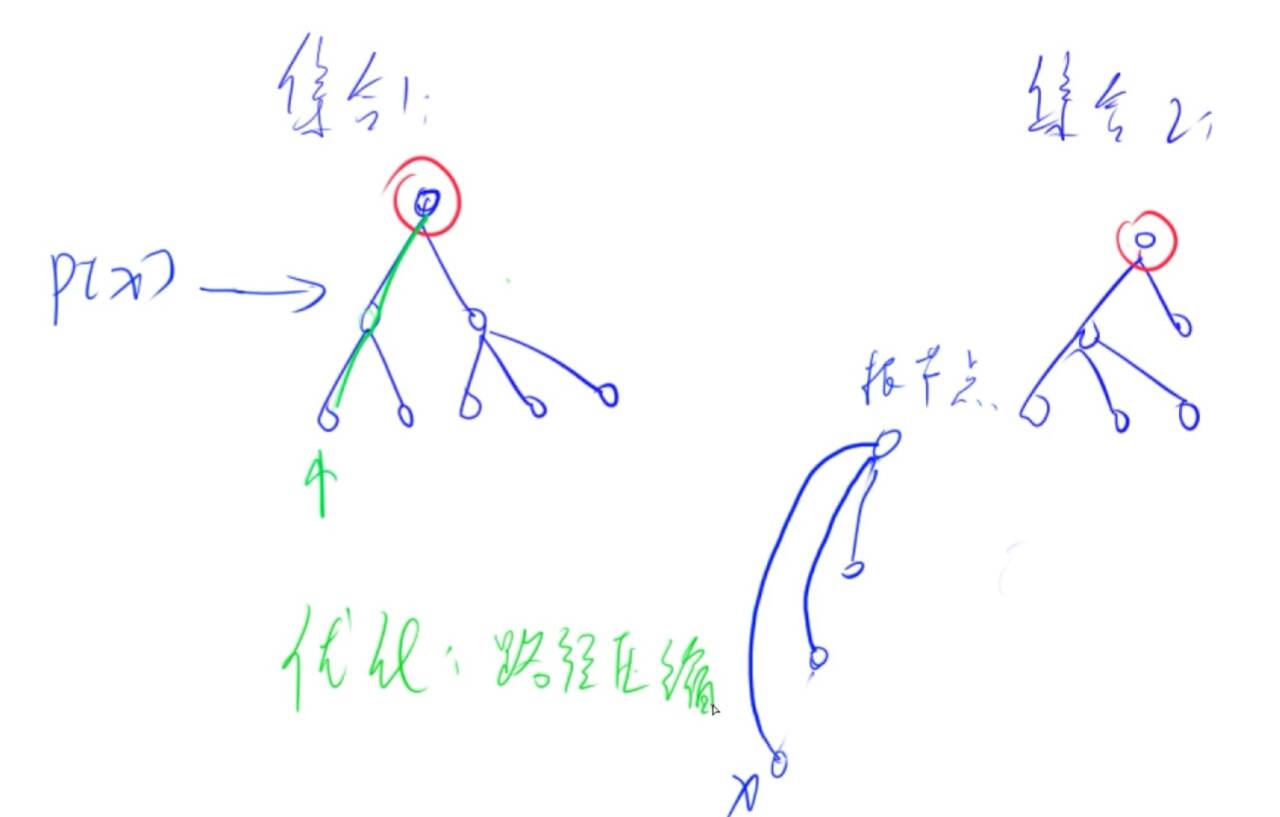
基本原理
每个集合用一棵树来表示
树根的编号为整个集合的编号
每个节点存储它的父节点->p[N]
问题1:如何判断树根 if(p[x]==x)
问题2:如何求x的集合编号 while(p[x]!=x) x=p[x]
问题3:如何合并两个集合
px是x的集合编号 py是y的集合编号
p[px]=py
核心代码:递归查找
int p[N];//记录父亲数组
int find(int x){//返回x所在集合的编号【祖宗节点】 + 路径压缩
if(p[x]!=x) p[x]=find(p[x]);//如果它不是根节点 -> 父节点=父节点的祖宗节点
return p[x];
}
【题目积累】
【并查集基本操作】Graph Composition
https://codeforces.com/contest/2060/problem/E
注意存边
注意操作顺序(先删边后连边)
思路

代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef pair<int,int> PII;
struct DSU{
vector<int> p,sz;
//建立并查集
DSU(int n):p(n + 1),sz(n + 1,1){for(int i = 1;i <= n;i++)p[i] = i;}
//找父亲+合并
int find(int x){return (p[x] == x) ? x : p[x] = find(p[x]);}
//查找是否相同
bool same(int x,int y){return find(x) == find(y);}
//合并两集合
bool merge(int x,int y){
x = find(x),y = find(y);
if(x == y)return false;
sz[x] += sz[y];
p[y] = x;
return true;
}
//查询集合内数量
int size(int x){return sz[find(x)];}
};
int t;
int n,m1,m2;
/*【思路】
删边:遍历F的每一条边 如果在G不连通就删掉 否则在F内连通
加边:遍历G的每一条边 如果在F不连通就加上
*/
void solve(){
cin>>n>>m1>>m2;
vector<PII> gg,ff;//存边
DSU f(n),g(n);//建立并查集
//先把所有边存下来
for(int i=1;i<=m1;i++){
int u,v;
cin>>u>>v;
if(u>v) swap(u,v);
ff.push_back({u,v});
}
for(int i=1;i<=m2;i++){
int u,v;
cin>>u>>v;
if(u>v) swap(u,v);
gg.push_back({u,v});
//建立连通性
g.merge(u,v);
}
ll ans=0;
for(int i=0;i<m1;i++){
int u=ff[i].first,v=ff[i].second;
if(g.same(u,v)) f.merge(u,v);
else ans++;
}
for(int i=0;i<m2;i++){
int u=gg[i].first,v=gg[i].second;
if(!f.same(u,v)){
ans++;
f.merge(u,v);
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--){
solve();
}
return 0;
}
【位运算优化n^2】隐匿社交网络
https://ac.nowcoder.com/acm/contest/100253/D
思路
看w数据范围 -> 每个数在二进制下最多64位(遍历64*n次即可)
->只要有一位一样就可以合并->当位有1就可以合并
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N=100010;
int t,n;
ll w[N];
struct DSU{
vector<int> p,sz;
//建立并查集
DSU(int n):p(n + 1),sz(n + 1,1){for(int i = 1;i <= n;i++)p[i] = i;}
//找父亲+合并
int find(int x){return (p[x] == x) ? x : p[x] = find(p[x]);}
//查找是否相同
bool same(int x,int y){return find(x) == find(y);}
//合并两集合
bool merge(int x,int y){
x = find(x),y = find(y);
if(x == y)return false;
sz[x] += sz[y];
p[y] = x;
return true;
}
//查询集合内数量
int size(int x){return sz[find(x)];}
};
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>w[i];
DSU q(n);
for(int i=63;i>=0;i--){//减少循环次数
int p=-1;//记录当前要合并进的集合
for(int j=1;j<=n;j++){
if(w[j]>>i&1){//取每一位
if(p!=-1) q.merge(p,j);
p=j;
}
}
}
int ans=-1;
for(int i=1;i<=n;i++) ans=max(ans,q.size(i));
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--){
solve();
}
return 0;
}
【图上的运用】在树上游玩
https://ac.nowcoder.com/acm/contest/100671/E
只涉及到边的题目:直接存边即可 不需要邻接表
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=100010;
const int mod=1e9+7;
int n,k;
int a[N];
int cnt[N];
struct DSU{
vector<int> p,sz;
//建立并查集
DSU(int n):p(n + 1),sz(n + 1,1){for(int i = 1;i <= n;i++)p[i] = i;}
//找父亲+合并
int find(int x){return (p[x] == x) ? x : p[x] = find(p[x]);}
//查找是否相同
bool same(int x,int y){return find(x) == find(y);}
//合并两集合
bool merge(int x,int y){
x = find(x),y = find(y);
if(x == y)return false;
sz[x] += sz[y];
p[y] = x;
return true;
}
//查询集合内数量
int size(int x){return sz[find(x)];}
};
vector<PII> deg;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
for(int i=1;i<=k;i++){
int cc;
cin>>cc;
a[cc]=1;
}
/*涉及到对边操作的都直接存边!!!*/
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
deg.push_back({u,v});
}
DSU dsu(n);
//枚举每条边:n-1条边所以可以枚举边
for(auto [u,v]:deg){
if(a[u]&&a[v]) dsu.merge(u,v);
}
//统计出边
for(auto [u,v]:deg){
if(!a[u] && a[v]) cnt[dsu.find(v)]++;//找到父亲再加:为统计连通块数量方便
if(!a[v] && a[u]) cnt[dsu.find(u)]++;
}
int res=0;
ll ans=1;
for(int i=1;i<=n;i++){
if(cnt[i]==0) continue;
res++;//注意这里查询连通块数目的方式!非常简洁
ans=ans*cnt[i]%mod;
}
cout<<res<<" "<<ans;
return 0;
}
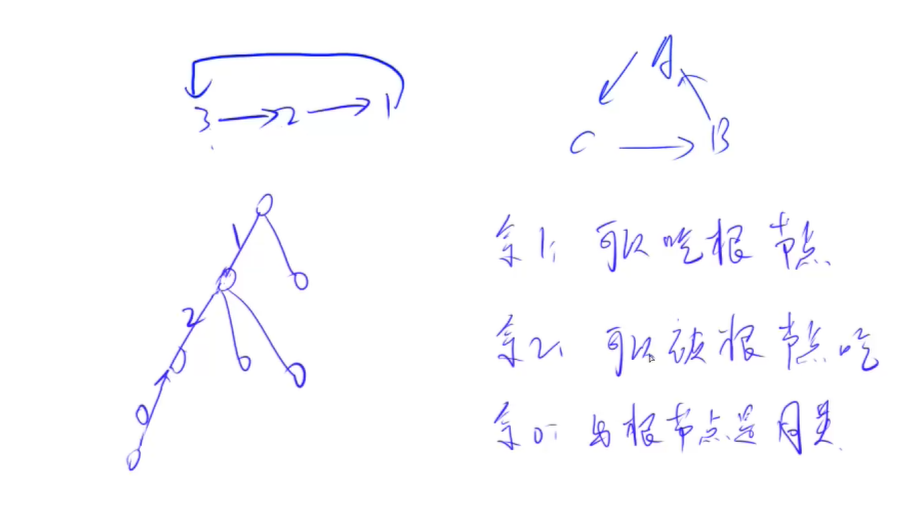
【带权并查集】食物链
题目来源:https://www.acwing.com/problem/content/242/
//【带权并查集】
/*【判断谁吃谁:与根节点距离】差值%3
余1 :可以吃根节点
余2 :可以被根节点吃
余0 : 与根节点同类
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,k;
int p[N],d[N];//d存储该节点到根节点的距离->有规律
int ans=0;
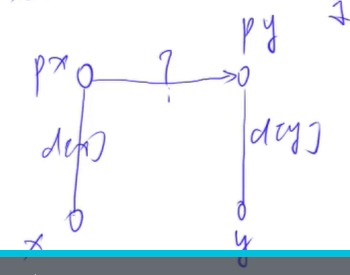
int find(int x){
if(p[x]!=x){
int t=find(p[x]);//p[x]不能先更新!
d[x]+=d[p[x]];//当前点到父节点的距离+父节点到根节点的距离=当前点到根节点的距离
p[x]=t;
}
return p[x];
}
int main(){
scanf("%d%d",&n,&k);
//预处理p数组!!!初始自己的祖宗节点都是自己!!!
for(int i=1;i<=n;i++) p[i]=i;
while(k--){
int a,x,y;
scanf("%d%d%d",&a,&x,&y);
if(x>n || y>n) ans++;
else{
int px=find(x),py=find(y);//先找到各自的节点
if(a==1){//判断同类
if(px==py && (d[x]-d[y])%3) ans++;//在同一个树里->两者差与3的模不为0->不成立为假话
else if(px!=py){//不在同一个树里:真话->变为同一个树
p[px]=py;
d[px]=d[y]-d[x];//与根节点距离相同:同类
}
}
else{
if(px==py && (d[x]-d[y]-1)%3) ans++;//x吃y->x=y+1为规律推出
else if(px!=py){
p[px]=py;
d[px]=d[y]+1-d[x];
}
}
}
}
printf("%d\n",ans);
return 0;
}
【维护点和边】Make it Forest
https://atcoder.jp/contests/abc399/tasks/abc399_c
注意merge内加边和维护边的操作
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=2e5+10;
int n,m;
bool st[N];
/*
并查集 该连通块
若边数>=点数 ans+=边数-点数+1
*/
struct DSU{
vector<int> p,sz1,sz2;
//建立并查集
DSU(int n):p(n + 1),sz1(n + 1,1),sz2(n+1,0){for(int i = 1;i <= n;i++)p[i] = i;}
//找父亲+合并
int find(int x){return (p[x] == x) ? x : p[x] = find(p[x]);}
//查找是否相同
bool same(int x,int y){return find(x) == find(y);}
//合并两集合
bool merge(int x,int y){
x = find(x),y = find(y);
if(x == y){
sz2[x]+=1;
return false;
}
sz2[x]+=sz2[y]+1;
sz1[x] += sz1[y];
p[y] = x;
return true;
}
//查询集合内数量
int size(int x){return sz1[find(x)];}
int size2(int x){
return sz2[find(x)];
}
};
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
DSU dsu(n+1);
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
dsu.merge(u,v);
}
/*
for(int i=1;i<=n;i++){
cout<<dsu.size(i)<<" ";
}
cout<<endl;
for(int i=1;i<=n;i++){
cout<<dsu.size2(i)<<" ";
}
*/
int ans=0;
for(int i=1;i<=n;i++){
int p=dsu.find(i);
if(!st[p]){
ans+=dsu.sz2[p]-dsu.sz1[p]+1;
}
st[p]=1;
st[i]=1;
}
cout<<ans;
return 0;
}
Disappearing Permutation
【只要涉及到多点关联关系的,都可以尝试并查集/连通块的思想解决问题】
https://codeforces.com/contest/2086/problem/C
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
int t;
int n;
struct DSU{
vector<int> p,sz;
//建立并查集
DSU(int n):p(n + 1),sz(n + 1,1){for(int i = 1;i <= n;i++)p[i] = i;}
//找父亲+合并
int find(int x){return (p[x] == x) ? x : p[x] = find(p[x]);}
//查找是否相同
bool same(int x,int y){return find(x) == find(y);}
//合并两集合
bool merge(int x,int y){
x = find(x),y = find(y);
if(x == y)return false;
sz[x] += sz[y];
p[y] = x;
return true;
}
//查询集合内数量
int size(int x){return sz[find(x)];}
};
void solve(){
cin>>n;
vector<int> p(n+1),d(n+1);
for(int i=1;i<=n;i++) cin>>p[i];
for(int i=1;i<=n;i++) cin>>d[i];
int ans=0;
DSU dsu(n);
for(int i=1;i<=n;i++){
dsu.merge(i,p[i]);
}
vector<bool> st(n+1,0);
for(int i=1;i<=n;i++){
int b=dsu.find(p[d[i]]);
if(!st[b]){
ans+=dsu.size(b);
cout<<ans<<" ";
st[b]=1;
}
else{
cout<<ans<<" ";
}
}
cout<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号