HDU 5130 Signal Interference --计算几何,多边形与圆的交面积

题意： 求所有满足PB <= k*PA 的P所在区域与多边形的交面积。

解法： 2014广州赛区的银牌题，当时竟然没发现是圆，然后就没做出来，然后就gg了。

圆的一般式方程：

 

设A(x1,y1),B(x2,y2),P(x,y)， 那么有

 

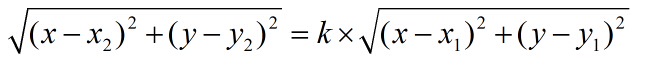
最后化成：

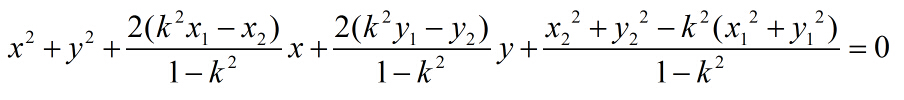
一般式里面的D,E,F自然就出来了，如果不记得一般式的话也可以自己推圆心和半径的，然后就是套的模板，模板的原理自己理吧。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define eps 1e-8
using namespace std;
#define N 100017

struct Point{
    double x,y;
    Point(double x=0, double y=0):x(x),y(y) {}
    void input() { scanf("%lf%lf",&x,&y); }
};
typedef Point Vector;
struct Circle{
    Point c;
    double r;
    Circle(){}
    Circle(Point c,double r):c(c),r(r) {}
    Point point(double a) { return Point(c.x + cos(a)*r, c.y + sin(a)*r); }
    void input() { scanf("%lf%lf%lf",&c.x,&c.y,&r); }
};
int dcmp(double x) {
    if(x < -eps) return -1;
    if(x > eps) return 1;
    return 0;
}
template <class T> T sqr(T x) { return x * x;}
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }
bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }
bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
Vector VectorUnit(Vector x){ return x / Length(x);}
Vector Normal(Vector x) { return Point(-x.y, x.x) / Length(x);}
double angle(Vector v) { return atan2(v.y, v.x); }

bool OnSegment(Point P, Point A, Point B) {
    return dcmp(Cross(A-P,B-P)) == 0 && dcmp(Dot(A-P,B-P)) < 0;
}
double DistanceToSeg(Point P, Point A, Point B)
{
    if(A == B) return Length(P-A);
    Vector v1 = B-A, v2 = P-A, v3 = P-B;
    if(dcmp(Dot(v1, v2)) < 0) return Length(v2);
    if(dcmp(Dot(v1, v3)) > 0) return Length(v3);
    return fabs(Cross(v1, v2)) / Length(v1);
}
double DistanceToLine(Point P, Point A, Point B){
    Vector v1 = B-A, v2 = P-A;
    return fabs(Cross(v1,v2)) / Length(v1);
}
Point DisP(Point A, Point B){
    return Length(B-A);
}
bool SegmentIntersection(Point A,Point B,Point C,Point D) {
    return max(A.x,B.x) >= min(C.x,D.x) &&
           max(C.x,D.x) >= min(A.x,B.x) &&
           max(A.y,B.y) >= min(C.y,D.y) &&
           max(C.y,D.y) >= min(A.y,B.y) &&
           dcmp(Cross(C-A,B-A)*Cross(D-A,B-A)) <= 0 &&
           dcmp(Cross(A-C,D-C)*Cross(B-C,D-C)) <= 0;
}

Point Zero = Point(0,0);
double TriAngleCircleInsection(Circle C, Point A, Point B)
{
    Vector OA = A-C.c, OB = B-C.c;
    Vector BA = A-B, BC = C.c-B;
    Vector AB = B-A, AC = C.c-A;
    double DOA = Length(OA), DOB = Length(OB),DAB = Length(AB), r = C.r;
    if(dcmp(Cross(OA,OB)) == 0) return 0;
    if(dcmp(DOA-C.r) < 0 && dcmp(DOB-C.r) < 0) return Cross(OA,OB)*0.5;
    else if(DOB < r && DOA >= r) {
        double x = (Dot(BA,BC) + sqrt(r*r*DAB*DAB-Cross(BA,BC)*Cross(BA,BC)))/DAB;
        double TS = Cross(OA,OB)*0.5;
        return asin(TS*(1-x/DAB)*2/r/DOA)*r*r*0.5+TS*x/DAB;
    }
    else if(DOB >= r && DOA < r) {
        double y = (Dot(AB,AC)+sqrt(r*r*DAB*DAB-Cross(AB,AC)*Cross(AB,AC)))/DAB;
        double TS = Cross(OA,OB)*0.5;
        return asin(TS*(1-y/DAB)*2/r/DOB)*r*r*0.5+TS*y/DAB;
    }
    else if(fabs(Cross(OA,OB)) >= r*DAB || Dot(AB,AC) <= 0 || Dot(BA,BC) <= 0) {
        if(Dot(OA,OB) < 0) {
            if(Cross(OA,OB) < 0) return (-acos(-1.0)-asin(Cross(OA,OB)/DOA/DOB))*r*r*0.5;
            else                 return ( acos(-1.0)-asin(Cross(OA,OB)/DOA/DOB))*r*r*0.5;
        }
        else                     return asin(Cross(OA,OB)/DOA/DOB)*r*r*0.5;
    }
    else {
        double x = (Dot(BA,BC)+sqrt(r*r*DAB*DAB-Cross(BA,BC)*Cross(BA,BC)))/DAB;
        double y = (Dot(AB,AC)+sqrt(r*r*DAB*DAB-Cross(AB,AC)*Cross(AB,AC)))/DAB;
        double TS = Cross(OA,OB)*0.5;
        return (asin(TS*(1-x/DAB)*2/r/DOA)+asin(TS*(1-y/DAB)*2/r/DOB))*r*r*0.5 + TS*((x+y)/DAB-1);
    }
}
//data segment
Point p[507],A,B;
//data ends

int main()
{
    int n,i,j,cs = 1;
    double k;
    while(scanf("%d%lf",&n,&k)!=EOF)
    {
        for(i=1;i<=n;i++) p[i].input();
        A.input(), B.input(), p[n+1] = p[1];
        double D = (2.0*k*k*A.x-2.0*B.x)/(1.0-k*k);
        double E = (2.0*k*k*A.y-2.0*B.y)/(1.0-k*k);
        double F = (B.x*B.x+B.y*B.y-k*k*(A.x*A.x+A.y*A.y))/(1.0-k*k);
        Circle C = Circle(Point(-D*0.5,-E*0.5),sqrt(D*D+E*E-4.0*F)*0.5);
        double ans = 0.0;
        for(i=1;i<=n;i++)
            ans += TriAngleCircleInsection(C, p[i], p[i+1]);
        printf("Case %d: %.10f\n",cs++,fabs(ans));
    }
    return 0;
}