导数 - 微分 -偏导数 - 偏微分 - 全微分

在一些数学公式的推导中，常会遇到 \(d\) / \(\partial\) / \(\delta\) \ \(\Delta\) 等符号。它们背后分别代表的数学含义？

---

增量

设变量 \(u\) 从它的一个初值 \(u_1\) 变到终值 \(u_2\)，终值与初值的差 \(u_2 - u_1\) 就叫做变量 \(u\) 的增量，记作 \(\Delta u\)，即

\[\Delta u = u_2 - u_1 \]

增量 \(\Delta u\) 可以是正的，也可以是负的。

应该注意到：记号 \(\Delta u\) 并不表示某个量 \(\Delta\) 与变量 \(u\) 的乘积，而是一个整体不可分割的记号。

举例：
现在假定函数 \(y = f(x)\) 在点 \(x_0\) 的某一个邻域内是有定义的。当自变量 \(x\) 在这个邻域内从 \(x_0\) 变到 \(x_0 + \Delta x\) 时，函数值（或因变量） \(f(x)\) 相应地从 \(f(x_0)\) 变到 \(f(x_0 + \Delta x)\)，因此，函数值（或因变量） \(f(x)\) 的对应增量为

\[\Delta y = f(x_0 + \Delta x) - f(x_0) \]

习惯上也称 \(\Delta y\) 为函数的增量。

由此，可以定义函数的连续性，如下：

设函数 \(y = f(x)\) 在点 \(x_0)\) 的某一个邻域内有定义，如果

\[\lim_{\Delta x \to 0} \Delta y = \lim_{\Delta x \to 0} [ f(x_0 + \Delta x) - f(x_0) ] = 0 \quad ， \]

那么就称函数 \(y = f(x)\) 在点 \(x_0\) 连续。

---

导数

导数的定义： 设函数 \(y = f(x)\) 在点 \(x_0\) 的某个邻域内有定义，当自变量 \(x\) 在 \(x_0\) 处取得增量 \(\Delta x\) （点 \(x_0 + \Delta x\) 仍在该邻域内）时，相应地，因变量取得增量 \(\Delta y = f(x_0 + \Delta x) - f(x_0)\)；如果 \(\Delta y\) 与 \(\Delta x\) 之比当 \(\Delta x \to 0\) 时的极限存在，那么称函数 \(y = f(x)\) 在点 \(x_0\) 处可导，并称这个极限为函数 \(y = f(x)\) 在点 \(x_0\) 处的导数，记为 \(f'(x)\) ，即

\[f'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \quad , \]

也可记作 \(y'|_{x = x_0}\)，$$\frac{dy}{dx}|_{x = x_0}$ 或 \(\frac{df(x)}{dx}|_{x=x_0}\)。

可以看出，导数等于 增量 \(\Delta y\) 和增量 \(\Delta x\) 比值的极限。

---

函数的微分

微分的定义： 设函数 \(y=f(x)\) 在某区间内有定义，\(x_0\) 及 \(x_0 + \Delta x\) 在这个区间内，如果函数的增量

\[\Delta y = f(x_0 + \Delta x) - f(x_0) \]

可表示为

\[\Delta y = A \Delta x + \mathit{o}(\Delta x) \]

其中，\(A\) 是不依赖于 \(\Delta x\) 的常数，那么，称函数 \(y=f(x)\) 在点 \(x_0\) 是可微的，而 \(A\Delta x\) 叫做函数 \(y = f(x)\) 在点 \(x_0\) 相应于自变量增量 \(\Delta x\) 的微分，即

\[dy = A \Delta x \]

注： 函数 \(f(x)\) 在点 \(x_0\) 可微的充要条件是函数 \(f(x)\) 在点 \(x_0\) 可导。

微分的意思是指，因变量的增量 \(\Delta y\)，是自变量的增量 \(\Delta x\) 的线性函数，且记作 \(dy\)。所以说，应该有如下关系：
增量 \(\Delta y\) 是实实在在、真实的变化值。只是，只有当可导的时候，才能写成 \(\Delta y = A \Delta x + \mathit{o}(\Delta x) = dy + \mathit{o}(\Delta x) = dy + \mathit{o}(dy)\) 。也就是说，微分，只是增量 \(\Delta y\) 的一个近似值。

另外一点，在定义导数的时候，也是用增量 \(\Delta y\) 与 \(\Delta x\) 的比值来定义的，并不是用微分。只是，导数的值，刚好等于微分 \(dy\) 与 \(dx\) 的比值。

注二： 通常把自变量 \(x\) 的增量 \(\Delta x\) 称为自变量的微分，记作 \(dx\)，即 \(dx = \Delta x\)。于是，函数 \(y = f(x)\) 的微分又可记作为

\[dy = f'(x) dx \]

从而有

\[\frac{dy}{dx} = f'(x) \]

这就是说，函数的微分 \(dy\) 与自变量的微分 \(dx\) 之商等于该函数的导数，因此，导数也叫作“微商”。

微分的几何意义

如下图所示，自变量的增量为 \(\Delta x = PR\) ，因变量的增量为 \(\Delta y = RQ\) 。那么，在 \(x_0\) 点作曲线的切线，则得到函数 \(y=f(x)\) 在点 \(x_0\) 相应于自变量增量 \(\Delta x\) 的微分 \(dy = RQ'\) 。

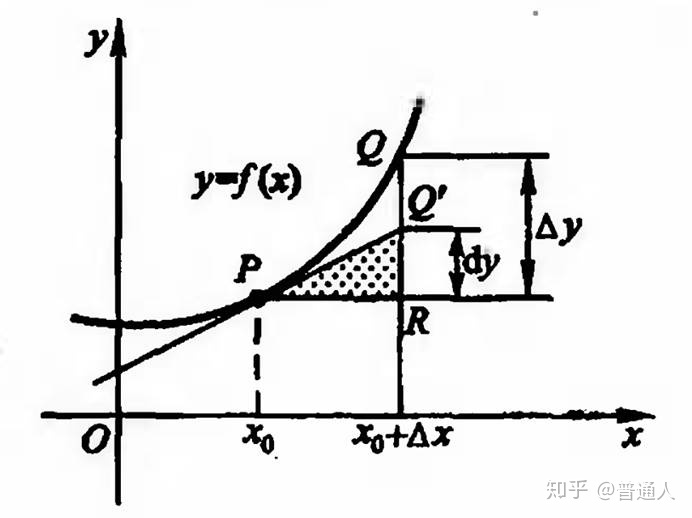
由此可见，对于可微函数 \(y = f(x)\) 而言，当 \(\Delta y\) 是曲线 \(y = f(x)\) 上的点的纵坐标的增量时，\(dy\) 就是曲线的切线上点的纵坐标的相应增量。
只是，当 \(|\Delta x|\) 很小时，$|\Delta y - dy| 比 $|\Delta x| 小得多。因此，在点 M 的邻近，我们可以用切线段来近似代替曲线段。在局部范围内用线性函数近似代替非线性函数，在几何上就是局部用切线段近似代替曲线段。这在数学上称为非线性函数的局部线性化，这是微分学的基本思想之一。

基本初等函数的微分公式与微分运算法则

从函数的微分表达式

\[dy = f'(x) dx \]

可以看出，要计算函数的微分，只要计算函数的导数，再乘自变量的微分。那么，可得到如下的微分公式和微分运算法则：

（略）

---

偏导数

偏导数的定义： 设函数 \(z=f(x,y)\) 在点 \((x_0, y_0)\) 的某一邻域内有定义，当 \(y\) 固定在 \(y_0\) 而 \(x\) 在 \(x_0\) 处有增量 \(\Delta x\) 时，相应的函数有增量

\[f(x_0 + x, y_0) - f(x_0, y_0) \]

如果

\[\lim{\Delta x \to 0} \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} \]

存在，那么称此极限为函数 \(z = f(x, y)\) 在点 \((x_0, y_0)\) 处对 \(x\) 的偏导数，记作

\[\frac{\partial z}{\partial x}\bigg|_{\begin{split} x=x_0 \\ y = y_0 \end{split}}, \quad \]

如果函数 \(z = f(x, y)\) 在区域 \(D\) 内每一个点 \((x, y)\) 处对 \(x\) 的偏导数都存在，那么这个偏导数就是 \(x\)，\(y\) 的函数，它就称为函数 \(z = f(x, y)\) 对自变量 \(x\) 的偏导函数，记作

\[\frac{\partial z}{\partial x}, \quad \frac{\partial f}{\partial x}, \quad 或 \quad f_x(x, y) \]

类似地，可以定义函数 \(z=f(x,y)\) 对自变量 \(y\) 的偏导函数，记作

\[\frac{\partial z}{\partial y}, \quad \frac{\partial f}{\partial y}, \quad 或 \quad f_y(x, y) \]

注：偏导数仍然是增量的比值。

偏导数的几何意义：偏导数 \(f_x(x, y)\) 的几何意义是曲面被平面 \(y = y_0\) 所截得的曲线在点 \(x_0\) 处的斜率。

---

偏微分 / 全微分

根据一元函数微分学中增量与微分的关系，可得

\[\begin{split} f(x+\Delta x, y) - f(x, y) \approx f_x(x, y) \Delta x, \\ f(x, y+\Delta y) - f(x, y) \approx f_y(x, y) \Delta y, \end{split}\]

上面两式的左端分别叫做二元函数对 \(x\) 和对 \(y\) 的偏增量，而右端分别叫做二元函数对 \(x\) 和对 \(y\) 的偏微分。

全增量： 设函数 \(z = f(x,y)\) 在点 \(P(x, y)\) 的某个邻域内有定义，\(P'(x + \Delta x, y+\Delta y)\) 为这个邻域内的任意一点，则称这两点的函数值之差 \(f(x+\Delta x, y+\Delta y) - f(x,y)\) 为函数在点 \(P\) 对应于自变量增量 \(\Delta x\) 和 \(\Delta y\) 的全增量，记作 \(\Delta z\) ，即

\[\Delta z = f(x +\Delta x, y+\Delta y) - f(x, y) \]

注：一般来说，计算全增量 \(\Delta z\) 比较复杂。与一元函数的情形类似，我们希望用自变量的增量 \(\Delta x\) 和 \(\Delta y\) 的线性函数来近似地代替函数的全增量 \(\Delta z\)，从而引入如下定义：

全微分的定义： 设函数 \(z = f(x, y)\) 在点 \((x, y)\) 的某个邻域内有定义，如果函数在点 \((x, y)\) 的全增量

\[\Delta z = f(x +\Delta x, y+\Delta y) - f(x, y) \]

可表示为

\[\Delta z = A\Delta x +B\Delta y +\mathit{o}(\rho) \]

其中，\(A\) 和 \(B\) 不依赖于 \(\Delta x\) 和 \(\Delta y\) 而仅与 \(x\) 和 \(y\) 有关，\(\rho = \sqrt{(\Delta x)^2 +(\Delta y)^2}\)，那么称函数 \(z=f(x,y)\) 在点 \((x,y)\) 可微分，而 \(A\Delta x + B\Delta y\) 称为函数 \(z=f(x,y)\) 在点 \((x, y)\) 的全微分，记作 \(dz\) ，即

\[dz = A\Delta x + B\Delta y \]

可微与可导的关系
定理1： 如果函数 \(z = f(x, y)\) 在点 \((x, y)\) 可微分，那么该函数在点 \((x, y)\) 的偏导数 \(\frac{\partial z}{\partial x}\) 与 \(\frac{\partial z}{\partial y}\) 必定存在，且函数 \(z = f(x, y)\) 在点 \((x, y)\) 的全微分为

\[dz = \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y \]

定理2： 如果函数\(z = f(x, y)\) 的偏导数 \(\frac{\partial z}{\partial x}\) 与 \(\frac{\partial z}{\partial y}\) 在点 \((x, y)\) 连续，那么该函数在该点可微分。

---

小结

总的来说，讲的是 增量、导数、微分 之间的关系。增量是变化的准确值，而微分，则是增量的一个近似值。导数，是该点处的斜率，也是增量比值的极限。