数据库系统概论——关系数据理论

函数依赖

• 函数依赖：X→Y的意义是对于X属性的相同的值，对应的Y的值一定是相同的，即X如果确定，一定可以通过X确定出Y
• 传递函数依赖：X→Y，Y→Z,且Y与Z不含于X，Z不含于Y，并且Y无法→X,则称Z传递依赖于X
• 候选键：能够决定R模式中的其他的所有关系，如果候选键多个，则可以选择一个为主码；含于任意候选键中的属性，称为主属性
• 闭包F+：F中的函数依赖所能推出的所有的函数依赖关系的集合
• 覆盖：F+=G+
• 属性闭包X+f：能够由X推出来的元素构成的集合（包括X）

规范形式

• 1NF:R中的属性值不能再分属性值
• 2NF：非主属性要求完全依赖于候选键，不可以部分依赖
• 3NF：候选键与非主属性之间不存在传递依赖
• BCNF：F中的袭来关系中存在左边不含有候选键的依赖

模式分解

模式分解即把一个关系R，分解成多个Ri，分解的过程中，要考虑分解的无损连接性以及保持依赖性两个问题

无损连接的检验算法

无损连接的定义在于将R关系分解成的n个小关系自然连接后如果仍与R保持一致则保证了无损连接

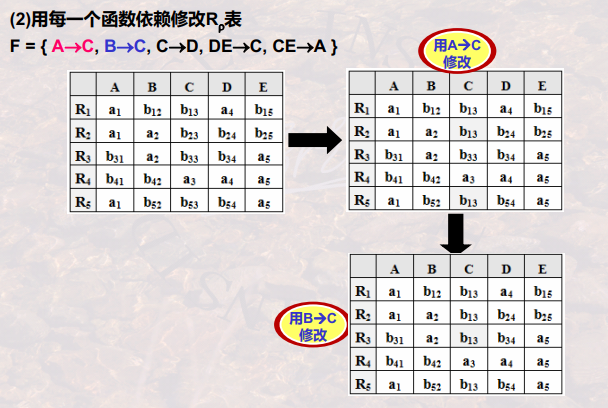
• 基本判断方法：将关系R（ABCDEF）中的每一个属性作为列项，将ρ=R{R1,R2,R3,....} 作为横项，F为函数依赖集合{A→B，B→C.....},针对于R1、R2中含有的属性项均标记为a，不含有的标记为b，形成初始化的列表，针对于A→B，A中属性值相同的行，B中的属性值也要要求相同。当将表修改完毕后，出现一行全部是a的项，则成为了无损连接，否则为有损链接。
  
  
  
• 特殊判定方法将R分解成R1、R2两个模式时的检验方法：如果R1与R2的交集能够决定R2——R1或者R1——R2时，则可以判断其是无损连接

保持依赖分解的检验算法

ρ=R{R1,R2,R3,....}，Ri所产生的函数依赖的∪产生的G覆盖F，即G+=F+，则可以说明分解保持依赖分解

分解为BCNF范式

• 普通分解BCNF:通过观察F，将含有候选键的关系组成Ri，其余的单独组成Ri
  

）先求最小依赖集，候码非码成子集 ）余下左侧全候码，完成BCNF题。
例.关系模式R,有U={A,B,C,D,E,G},F={B->G,CE->B,C->A,CE->G,B->D,C->D}，将关系模式分解BCNF

第一步：先求最小依赖集。可以发现CE->G多余，因此最小依赖集为F={B->G,CE->B,C->A,B->D,C->D}。

第二步：候码非码成子集。由于候选码为(CE)因此将CE->B划分出子集（BCE），而B->G，B->D左侧均不含主属性(C、E)中的任何一个故划分出(BG),(BD）

第三步：此时剩余依赖F={C->A,C->D}剩余元素{A,C,D}检查发现函数依赖左侧都是候选码即完成BCNF分解，如果不满足则继续分解余下的。

于是BCNF分解的最后结果为{（BG）,(BD),(ACD),(BCE)}。

• 无损连接分解BCNF：从R中不断地将不满足BCNF模式的关系拿出来单独形成一个Ri，直到剩余的模式是BCNF为止
  

分解为BCNF并保持无损连接的例子
关系模式R<U,F>，其中：U={A,B,C,D,E}， F={A→C,C→D,B→C,DE→C,CE→A}，将其分解成BCNF并保持无损连接。
① 令ρ={R(U,F)}。

② ρ中不是所有的模式都是BCNF，转入下一步。

③ 分解R：R上的候选关键字为BE（因为所有函数依赖的右边没有BE）。考虑A→C函数依赖不满足BCNF条件（因A不包含候选键BE），将其分解成R1(AC)、R2(ABDE)（(U-C)(A)）。计算R1和R2的最小函数依赖集分别为：F1={A→C}，F2={B→D,DE→D,BE→A}（這個不是Fm，衹是它的一個等價）。其中B→D是由于R2中没有属性C且B→C,C→D；DE→D是由于R2中没有属性C且DE→C,C→D；BE→A是由于R2中没有属性C且B→C,CE→A。又由于DE→D是蕴含关系，可以去掉，故F2={B→D,BE→A}。

分解R2：R2上的候选关键字为BE。考虑B→D函数依赖不满足BCNF条件，将其分解成R21(BD)、R22(ABE)。计算R21和R22的最小函数依赖集分别为：F21={B→D}，F22={BE→A}。

分解成3NF范式

F中的每一个依赖单独构成一个模式，而后考虑能够合并

• 保持依赖分解3NF：先对依赖集F进行一个极小化处理，将F中未能出现的属性放在一起构成一个关系模式Ri，其余的单独成为一个模式，若X决定Y，X决定Z，则{XYZ}构成一个模式
• 既保持依赖，又无损连接：上述算法产生的模式中，存在一个模式含有候选键，则可以在保持依赖的基础上保持无损连接
  
  

分解为依赖又无损连接的3NF的例题
已知R(ABCDE), F={A ->D,E->D,D->B,BC->D,DC->A}求保持函数依赖的3NF分解，和具有无损连接性及保持函数依赖的3NF分解

第一步：保函依赖分解题，先求最小依赖集。先求出R的最小依赖集，可得F={A ->D,E->D,D->B,BC->D,DC->A}

第二步：依赖两侧未出现，分成子集放一边。首先可以发现没有不出现在两侧的元素不用单独分出一个子集，“剩余依赖变子集”然后我们将各依赖分别划分为子集得到：{AD} {ED} {DB} {BCD} {DCA}，即为所求保持函数依赖的3NF分解

第三步：若要连接成无损，再添候选做子集。

(1)候选码的求解：所谓候选码即能决定整个关系的，我们通过找未出现在依赖右边的和两侧均未出现的元素即可求得，

(2)可以发现C E未出现在右边，因此候选码为{CE}。故所求具有无损连接性及保持函数依赖的3NF分解为{AD} {ED} {DB} {BCD} {DCA} {CE}

————————————————

例子链接：https://blog.csdn.net/qq_26769591/article/details/60327723
————————————————
例子连接：https://blog.csdn.net/sumaliqinghua/article/details/86246762