MO 复健

不定期传一些最近写的 MO 题．

1. 如图，在锐角 \(\triangle ABC\) 中，\(O, H\) 分别是外心和垂心，\(K\) 是 \(AH\) 的中点，\(P\) 在 \(AC\) 上，且满足 \(\angle BKP = 90^\circ\)．求证：\(OP \parallel BC\)．

   

   证明：

   

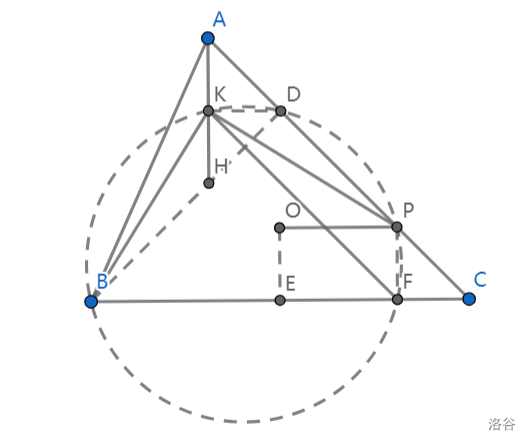
   如图，作直线 \(BH\) 交 \(AC\) 于点 \(D\)，连结 \(KD\)；分别过 \(O, P\) 作 \(BC\) 的垂线交于 \(E, F\)．

   由 \(\angle BKP = \angle BDP = \angle BFP\)，知 \(B, F, P, D, K\) 五点共圆．在 \(\text{Rt}\triangle HDA\) 中，\(KD = KH = \displaystyle \frac{AH}{2}\)，\(\angle KDA = \angle KAD = 90^\circ - \angle C\)，故 \(\angle KDP = 90^\circ + \angle C\)．

   又 \(\angle CPF = 90^\circ - \angle C\)，知 \(\angle DPF = 90^\circ + \angle C = \angle KDP\)，结合四点共圆，知四边形 \(PDKF\) 为等腰梯形．由此，\(PF = DK = \displaystyle \frac{AH}{2}\)．又 \(OE = R \cdot \cos A, AH = AB \cdot \cos A \cdot \sec (90^\circ - C) = 2R \cos A \Rightarrow OE = \displaystyle \frac{AH}{2} = PF\)，\(OE \perp BC, PF \perp BC \Rightarrow OE \parallel PF\)，知四边形 \(OEFP\) 是平行四边形，于是 \(OP \parallel BC\)，得证．

2. 如图，\(\triangle ABC\) 内接于 \(\odot O\)，\(AA'\) 为 \(BC\) 边上的高，\(X\) 在射线 \(AA'\) 上，\(\angle BAC\) 的平分线交 \(\odot O\) 于 \(D\)，\(N\) 在 \(XD\) 的延长线上，且满足 \(ON \parallel AD\)，\(M\) 是 \(XD\) 的中点．求证：\(\angle BAM = \angle CAN\)．

   

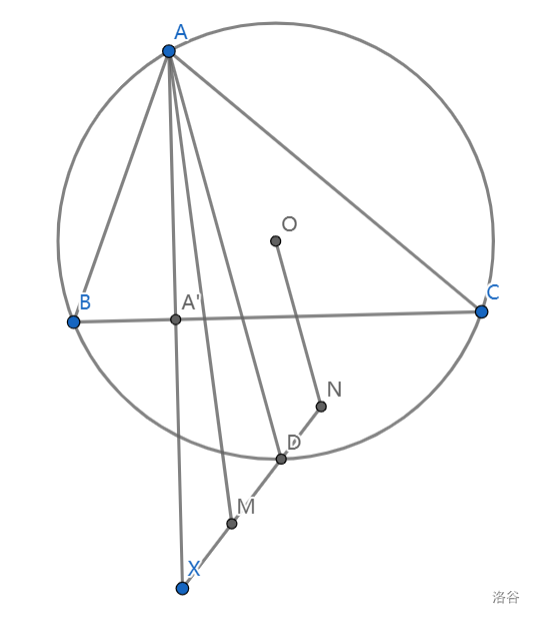
   证明：

   

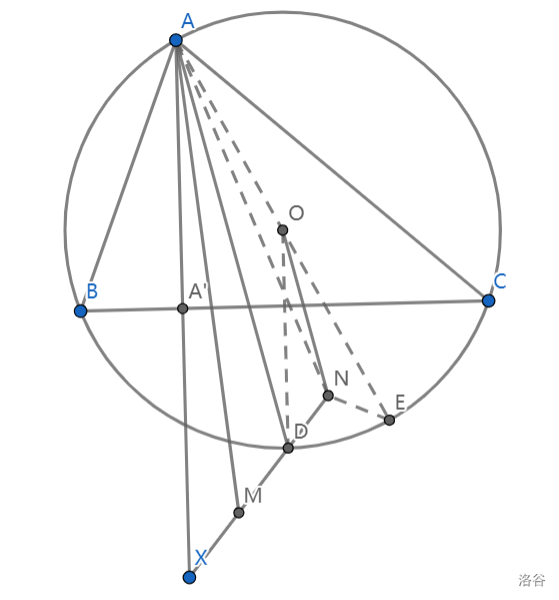
   如图，连结 \(AO\) 并延长交 \(\odot O\) 于点 \(E\)，连结 \(OD, NE, AN\)．

   由于 \(\angle BAX = 90^\circ - \angle B = \angle CAO\)，故 \(AD\) 平分 \(\angle XAE\)．又 \(OD \parallel AX, ON \parallel AD\)，得 \(ON\) 平分 \(\angle DOE\)．又 \(OD = OE\)，\(N\) 在角平分线上，知 \(\triangle ODN \cong \triangle OEN\)．而 \(AX \parallel OD\)，知 \(\triangle AXD \sim \triangle ODN \Rightarrow \triangle AXD \sim \triangle OEN \Rightarrow \displaystyle \frac{AX}{XD} = \frac{OE}{EN} \Rightarrow \frac{AX}{XM} = \frac{AE}{EN}\)．又 \(\angle AXD = \angle ODN = \angle OEN\)，知 \(\triangle AXM \sim \triangle AEN\)，于是 \(\angle XAM = \angle EAN \Rightarrow \angle BAM = \angle CAN\)．证毕．

3. \(a, b, c \in R_+\)，\(abc = 1\)，求证：\((a + b)(b + c)(c + a) \geq 4(a + b + c - 1)\)．

   证明：设 \(p = a + b + c, q = ab + bc + ca, r = abc = 1\)．则要证 \(pq - r \geq 4(p - 1)\)．

   由 \(r = 1\)，只需证 \(pq + 3 \geq 4p\)，又由舒尔不等式，\(q^2 \geq 3pr, r = 1 \Rightarrow q \geq \sqrt{3p}\)，只需证 \(p\sqrt{3p} + 3 \geq 4p\)，整理平方得 \(3p^3 - 16p^2 + 24p - 9 \geq 0\)．设 \(f(x) = 3x^3 - 16x^2 + 24x - 9 = (x - 3)(3x^2 - 7x + 3)\)，则 \(f(3) = 0\)，\(f'(x) = 9x^2 - 32x + 24\)，当 \(x \geq 3\) 时，易知 \(f'(x) \geq 0\)，于是 \(f(x) \geq 0\)，那么只需证 \(p \geq 3\)．而 \(p^2 \geq 3q \geq 3\sqrt{3p} \Rightarrow p \geq 3\)，得证．

4. 如图，\(\triangle ABC\) 中，\(AB = AC\)，\(D\) 为 \(BC\) 中点，过点 \(B\) 的 \(\odot O\) 分别交 \(AB, AD, BC\) 于 \(L, M, N\)，\(MN\) 交 \(AC\) 于 \(K\)，过 \(C\) 作 \(LN\) 的平行线分别交 \(AD, KL\) 于 \(S, T\)，证明：\(M, T, B, S\) 共圆．

   

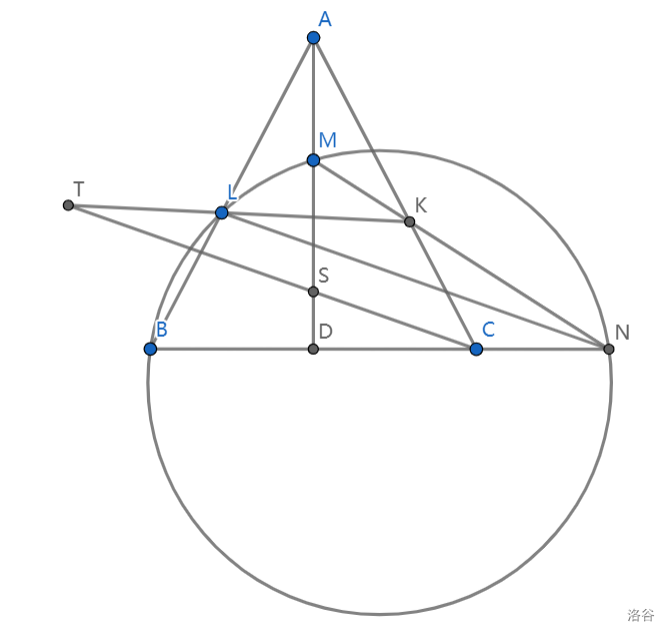
   证明：

   

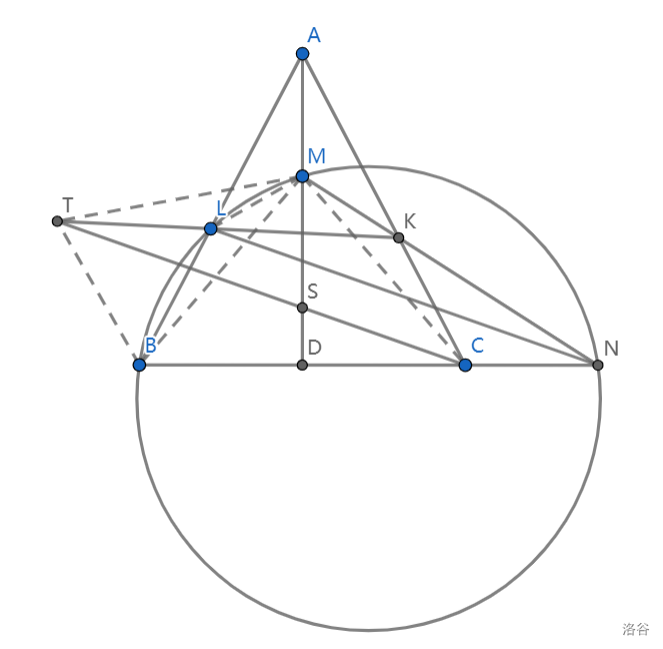
   如图，连结 \(MT, MB, MC, ML\)．易知 \(MB = MC\)．

   \(\angle LMN = 180^\circ - \angle LBN = 180^\circ - (90^\circ - \displaystyle \frac{\angle A}{2}) = 90^\circ + \frac{\angle A}{2}\)，故 \(M\) 是 \(\triangle ALK\) 的内心，于是 \(\angle CKN = \angle AKM = \angle MKL, \angle CNK = \angle ALM = \angle MLK\)，故 \(\triangle KCN \sim \triangle KML\)，则有 \(\triangle KMC \sim \triangle KLN\)，所以 \(\angle KMC = \angle KLN = \angle KTC(LN \parallel TC)\)，故 \(K, M, T, C\) 四点共圆．

   \(\angle MTC = \angle NKC = \angle AKM = \angle MKT = \angle MCT \Rightarrow MT = MC = MB\)，故 \(M\) 是 \(\triangle TBC\) 的外心，\(\angle BTS = \angle BTC = \displaystyle \frac{\angle BMC}{2} = \angle BMS\)，故 \(M, T, B, S\) 四点共圆．证毕．

5. 如图，完全四边形 \(ABCDEF\) 中，\(\angle A = 90^\circ\)，点 \(O\) 为 \(\triangle BCE\) 外心，\(\triangle CDF\) 的外接圆 \(\odot P\) 交 \(OD\) 于另一点 \(K\)，证明：\(\angle FDB = \angle FKB\)．

   

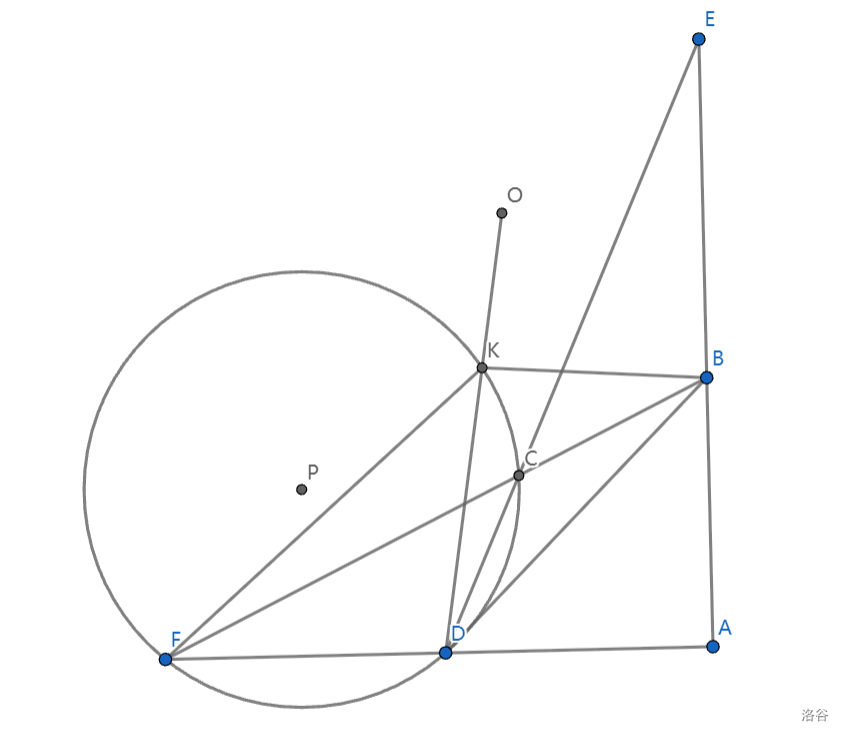
   证明：

   

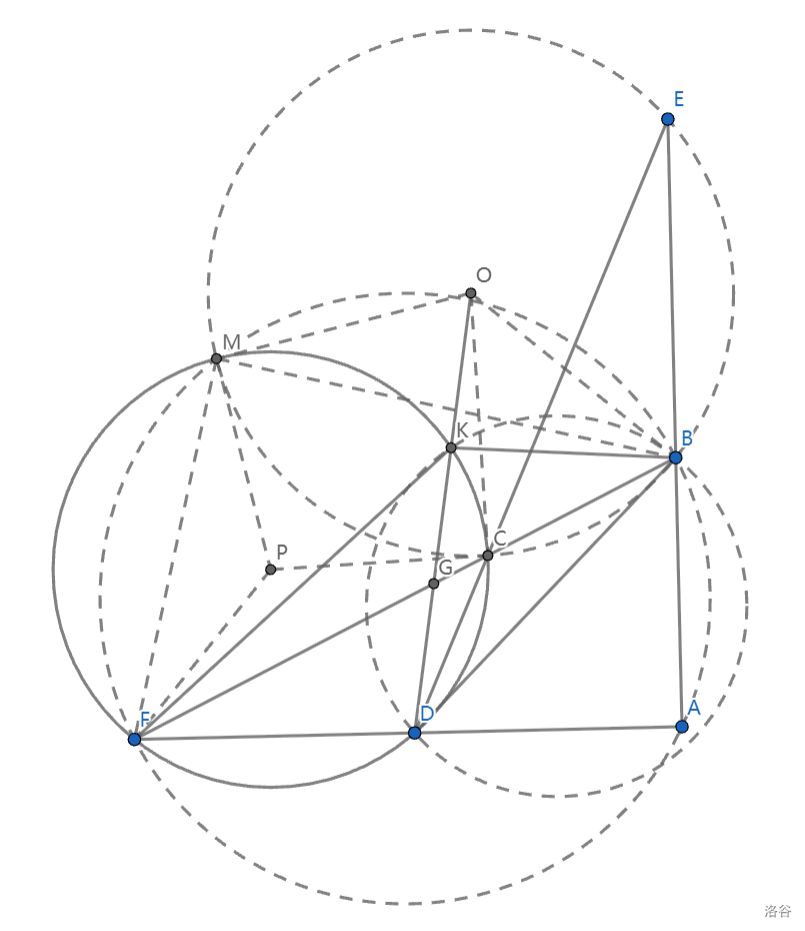
   如图，作出 \(\triangle CBE\) 的外接圆，交 \(\odot P\) 于点 \(M\)，\(OD\) 交 \(BF\) 于点 \(G\)，连结图中线段．

   由密克定理，\(M, C, B, E\)、\(M, F, A, B\) 分别四点共圆．\(\angle MPF = 2\angle MDF = 2\angle MEA = 2\angle MEB = \angle MOB\)，又 \(MP = FP, MO = BO\)，故 \(\triangle MFP \sim \triangle MBO\)，于是 \(\triangle PMO \sim \triangle FMB\)，故 \(\angle PMO = \angle FMB = 180^\circ - \angle A = 90^\circ\)．于是 \(\odot O, \odot P\) 正交，\(OC\) 是 \(\odot P\) 的切线．

   由圆幂定理，\(OC^2 = OK \cdot OD\)，又 \(OB = OC\)，知 \(OB^2 = OK \cdot OD\)，于是 \(OB\) 是 \(\triangle KDB\) 的切线，有 \(\angle OBK = \angle BDK\)．

   \(\angle KBF - \angle DBF = \angle BFD + \angle BDF - \angle BFK - \angle BKF\)．而 \(\angle KBF - \angle DBF = \angle OBC - \angle OBK - \angle DBF = (90^\circ - \angle BMC) - \angle KDB - \angle DBF = \angle FMC - \angle FGD = \widehat{FC} - \widehat{FD} + \widehat{KC} = \widehat{CD} - \widehat{KC} = \angle CFD - \angle CFK = \angle BFD - \angle BFK\)，带回前式知 \(\angle BDF - \angle BKF = 0\)，于是 \(\angle FDB = \angle FKB\)，证毕．

6. \(a, b, c \in R_+\)，求证：\(\displaystyle \sum \frac{1}{a^3 + b^3 + abc} \leq \frac{1}{abc}\)．

   证明：原式 \(\Leftrightarrow \displaystyle \sum \frac{abc}{a^3 + b^3 + abc} \leq 1 \Leftrightarrow \sum \frac{1}{\frac{a^2}{bc} + \frac{b^2}{ac} + 1} \leq 1\)，令 \(x = \displaystyle \frac{a^2}{bc}, y = \frac{b^2}{ac}, z = \frac{c^2}{ab}\)，则 \(xyz = 1\)，原式 \(\Leftrightarrow \displaystyle \sum \frac{1}{x + y + 1} \leq 1\)，两边通分并整理得原式 \(\Leftrightarrow \displaystyle \sum xy(x + y) - 2\sum x + y \geq 0 \Leftrightarrow \sum (xy - 1)(x + y) \geq 0\)．不妨设 \(x \geq y \geq z\)，显然 \(x + y \geq x + z \geq y + z, xy - 1 \geq xz - 1 \geq yz - 1\)．对上式使用排序不等式，有 \(\displaystyle \sum(xy - 1)(x + y) \geq \frac{2}{3}(\sum xy - 3)\sum x\)，而 \(\displaystyle \sum xy - 3 \geq 3\sqrt[3]{x^2y^2z^2} - 3 = 0\)，\(\displaystyle \sum x \geq 0\)，有 \(\displaystyle \sum(xy - 1)(x + y) \geq \frac{2}{3}(\sum xy - 3)\sum x \geq 0\)，故原式成立，证毕．

7. \(x, y, z \in R_+\)，\(xyz \geq 1\)，求证：\(\displaystyle \sum \frac{x^5 - x^2}{x^5 + y^2 + z^2} \geq 0\)．

   证明：

   ​ 引理 \(1\)：对 \(x, y > 0\)，有 \(x^4 + y^4 \geq x^3y + xy^3\)．

   ​ 引理 \(1\) 证明：\(x^4 + y^4 \geq x^3y + xy^3 \Leftrightarrow x^4 + y^4 - x^3y - xy^3 \geq 0 \Leftrightarrow (x - y)^2(x^2 + xy + y^2) \geq 0\) 显然成立，得证．

   ​ 引理 \(2\)：对 \(x, y, z > 0\)，有 \(x^4 + y^3z + yz^3 \geq xyz(x + y + z)\)

   ​ 引理 \(2\) 证明：

   \[x^4 + y^3z + yz^3 = (2 \cdot \frac{x^4}{4} + \frac{y^3z}{4} + \frac{yz^3}{4}) + (2 \cdot \frac{x^4}{8} + 5 \cdot \frac{y^3z}{8} + \frac{yz^3}{8}) + (2 \cdot \frac{x^4}{8} + \frac{y^3z}{8} + 5 \cdot \frac{yz^3}{8}) \\ \geq 4\sqrt[4]{\frac{x^8y^4z^4}{4^4}} + 8\sqrt[8]{\frac{x^8y^{16}z^8}{8^8}} + 8\sqrt[8]{\frac{x^8y^8z^{16}}{8^8}} \\ = x^2yz + xy^2z + xyz^2 = xyz(x + y + z) \]

   ​ 得证．

   回到原题．原式 \(\Leftrightarrow \displaystyle \sum \frac{x^5}{x^5 + y^2 + z^2} \geq \sum \frac{x^2}{x^5 + y^2 + z^2}\)．

   由 \(xyz \geq 1\) 及引理 \(1\)，有 \(\displaystyle \frac{x^5}{x^5 + y^2 + z^2} \geq \frac{x^5}{\frac{x^5}{xyz} + y^2 + z^2} = \frac{x^5yz}{x^4 + y^3z + yz^3} \geq \frac{x^5yz}{x^4 + y^4 + z^4}\)，同理有 \(\displaystyle \frac{y^5}{x^2 + y^5 + z^2} \geq \frac{xy^5z}{x^4 + y^4 + z^4}\)、\(\displaystyle \frac{z^5}{x^2 + y^2 + z^5} \geq \frac{xyz^5}{x^4 + y^4 + z^4}\)，

   则 \(\displaystyle \sum \frac{x^5}{x^5 + y^2 + z^2} \geq \sum \frac{x^5yz}{x^4 + y^4 + z^4} = \frac{xyz(x^4 + y^4 + z^4)}{x^4 + y^4 + z^4} = xyz \geq 1\)．

   由 \(xyz \geq 1\) 及引理 \(2\)，有 \(\displaystyle \frac{x^2}{x^5 + y^2 + z^2} \leq \frac{x^2}{x^5 + xy^3z + xyz^3} = \frac{x}{x^4 + y^3z + yz^3} \leq \frac{x}{xyz(x + y + z)}\)，同理有 \(\displaystyle \frac{y^2}{x^2 + y^5 + z^2} \leq \frac{y}{xyz(x + y + z)}\)、\(\displaystyle \frac{z^2}{x^2 + y^2 + z^5} \leq \frac{z}{xyz(x + y + z)}\)，

   则 \(\displaystyle \sum \frac{x^2}{x^5 + y^2 + z^2} \leq \sum \frac{x}{xyz(x + y + z)} = \frac{x + y + z}{xyz(x + y + z)} = \frac{1}{xyz} \leq 1\)．

   故 \(\displaystyle \sum \frac{x^5}{x^5 + y^2 + z^2} \geq 1 \geq \sum \frac{x^2}{x^5 + y^2 + z^2}\)，原式得证．