关于float和double类型数据在单片机内存中如何存储和转换

关于float和double类型数据在单片机内存中如何存储和转换

1、单精度浮点型float，双精度浮点型double数据在内存中的存储模型

（1）下图为单精度浮点型数据float的存储模型，符号位S在最高位，占用1bit内存，指数位E占用8bits内存，底数部分M占用23bits内存，总共占用4个字节：

（2）下图为双精度浮点型数据double的存储模型，符号位S在最高位，占用1bit内存，指数位E占用11bits内存，底数部分M占用52bits内存,总共占用8个字节：

解释说明：
（一）符号位S：符号位表示浮点型数据的正负，0表示正数，1表示负数，如6.24的符号位S为0，-6.24的符号位S为1；
（二）指数位E：指数位E即2的次方数，如 float n = 6.24，可以表示为
（这里的底数未写全）。这里，E = 2。但是，IEEE754标准中规定E为一个无符号整型，而现实中科学计数法指数位E可能为负数，因此，这里引入了中间值的概念。对于单精度浮点型数据float，E的中间值为127；对于双精度浮点型数据double，E的中间值为1023。在对E进行存储时，需要将其真实值加上中间值后再存入内存。如，6.24的指数位真实值E = 2，则存入内存应为E = 2 + 127(中间值) = 129（这里转为二进制是 10000001 ）。再比如，真实指数位E = -2时，存入内存应为 E = -2 + 127 =125；
（三）底数位M：M位可理解为有效数据（或者称为底数部分），其取值范围是1≤M<2，因为M小数点前面的数永远为1，为了增加浮点型数据的精度及可表示的数据的范围，IEEE754标准规定M在内存中只存储小数点后边的位，如float n =6.24表示为
（这里的底数未写全），M = 1. 10001111010111000010100，写入内存时舍去小数点前面的1，仅存入10001111010111000010100 (占用23位)。

举例说明单精度浮点型数据转换为16进制的方法：

例如：float n=6.24，二进制表示（转换为二进制方法见附录）为
110.0011110101110000101000111101011100001010001111011
将其转化为科学计数法：
1.100011110101110000101000111101011100001010001111011e2
根据以上信息可得：
符号位S：0 B
指数位E：10000001 B
底数位M：10001111010111000010100 B
将以上二进制位拼接起来就是
0100 0000 1100 0111 1010 1110 0001 0100B=0x40C7AE14
即以上就是单精度浮点型数据转换为16进制的方法；

2、16进制转换为float类型数据

同样的根据0x40C7AE14举例说明转换为float数据，首先根据底数位M：
10001111010111000010100 B
转换为小数部分为（2进制转为10进制）：

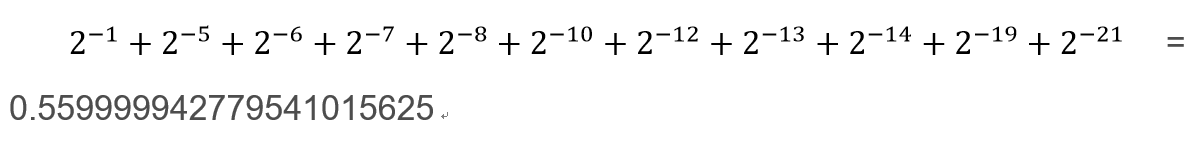
然后还要加上内存不记录的1，所以得到科学计数法里的底数为 1.559999942779541015625
又因为指数E=129-127=2，所以根据公式得到float类型数据为：

由于精度原因，与最初设置的6.24有一定误差，这是正常现象；

3、单片机中如何将float类型数据存储到内存

（1）创建float类型数据的共用体
typedef union
{
float f_num;
char h_num[4];
} Data_Typedef;

（2）指针转换
float data;
uint32_t temp;
temp = *(uint32_t *)&data;

4、四字节数组转为float

/**
*作用：把u8四字节数组转为float
*note：低地址放float的低字节
*/
float ByteToFloat(u8 str)
{
float data;
data = ((float)str);
return data;
}

附录1：将一个float型转化为内存存储格式的步骤

 （1）先将这个实数的绝对值化为二进制格式。 
 （2）将这个二进制格式实数的小数点左移或右移n位，直到小数点移动到第一个有效数字的右边。 
 （3）从小数点右边第一位开始数出二十三位数字放入第22到第0位。 
 （4）如果实数是正的，则在第31位放入“0”，否则放入“1”。 
 （5）如果n 是左移得到的，说明指数是正的，第30位放入“1”。如果n是右移得到的或n=0，则第30位放入“0”。 
 （6）如果n是左移得到的，则将n减去1后化为二进制，并在左边加“0”补足七位，放入第29到第23位。
	   如果n是右移得到的或n=0，则将n化为二进制后在左边加“0”补足七位，再各位求反，再放入第29到第23位。

附录2：将一个内存存储的float二进制格式转化为十进制的步骤

 （1）将第22位到第0位的二进制数写出来，在最左边补一位“1”，得到二十四位有效数字。将小数点点在最左边那个“1”的右边。 
 （2）取出第29到第23位所表示的值n。当30位是“0”时将n各位求反。当30位是“1”时将n增1。 
 （3）将小数点左移n位（当30位是“0”时）或右移n位（当30位是“1”时），得到一个二进制表示的实数。 
 （4）将这个二进制实数化为十进制，并根据第31位是“0”还是“1”加上正号或负号即可。

附录3：整数和小数的二进制表示

 (1)  十进制整数如何转化为二进制数
       算法很简单。举个例子，11表示成二进制数：
                 11/2=5   余   1
                   5/2=2   余   1
                   2/2=1   余   0
                   1/2=0   余   1
                      0结束         
				11二进制表示为(从下往上):1011
  (2) 十进制小数如何转化为二进制数
       算法是乘以2直到没有了小数为止。举个例子，0.9表示成二进制数
                 0.9*2=1.8   取整数部分  1
                 0.8(1.8的小数部分)*2=1.6    取整数部分  1
                 0.6*2=1.2   取整数部分  1
                 0.2*2=0.4   取整数部分  0
                 0.4*2=0.8   取整数部分  0
                 0.8*2=1.6   取整数部分  1
                 0.6*2=1.2   取整数部分  0
	.........      0.9二进制表示为(从上往下): 1100100100100......