C语言第八章数组

上节回顾：

变量的作用域和存储类型

变量的作用域：可被访问的范围，分为局部变量和全局变量

变量的存储类型：变量在内存中被分配内存的方式，分为静态存储区、动态存储区

变量的存储类型决定变量的存储周期，静态存储区分配内存的变量生命周期比较长

 

auto：动态局部变量，容易与(static)静态局部变量，两者作用域相同，但是生存周期不一样。动态局部变量离开语句块再次进入该语句块，变量的值就消失了，变为随机值；而静态局部变量，下次再进入语句块，值仍然保留。动态局部变量每次进入语句块都需要初始化，否则是随机值；而静态局部变量则只需要初始化一次，如果不显式初始化的话，则默认初始化为0.

 

第八章   数组

函数之前，自底向上的设计，函数之后，自顶向下的设计。

数组之前，简单的数据结构。

数组之后，复杂的数据结构。

 

为什么要学习数组呢？

如果要读入十个数据，需要十个变量一个一个读取，用数组可以循环读入，只需要一条scanf语句。

数组适合处理大量的有相同数据类型的问题

 

一维数组的定义和初始化

int a[10];定义一个有10个元素的一维数组，编译器分配10个连续的整形存储空间，首地址用数组名来表示，即a。

 

不能定义一个动态可变长度的数组，一旦定义，就不能改变其长度。因此，在标准C中是不允许将数组下标定义成变量的。可以使用宏定义的方式来实现数组长度的修改。

 

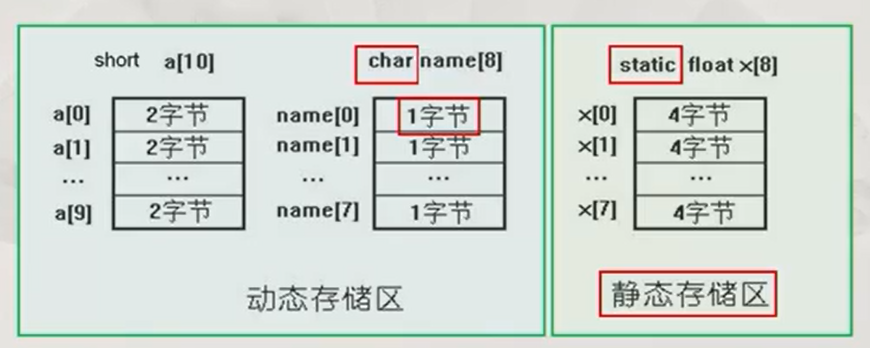
根据数组的数据类型，为每一元素安排相应字节数的存储空间。

根据数组的存储类型，将其安排在内存的动态、静态存储区或者寄存器区。

 

一维数组的引用

允许快速随机访问，可以使用变量或者表达式，如a[i]。

 

未初始化的数组元素的值是什么？

静态数组和全局数组会自动初始化为0，其他的是随机值。

 

一维数组的初始化

 

怎么判断两个数组相等，或者说怎么把一个数组的值赋值给另外一个数组？

使用循环语句赋值即可。

更高效的数组初始化方法：用sizeof（a）获取数组a所占内存的字节数。

memset(a,0,sizeof(a));

更搞笑的数组赋值方法：将a数组的值赋给b

memcpy(b,a,sizeof(a));

使用以上两个函数，需要使用string.h头文件

 

例：编程实现用户输入月数显示天数（不考虑闰年）

  

访问数组的时候，下标越界是大忌，编译的时候不会报错，会发生运行时错误！！

当下标小于0或者越界的时候会出现什么情况？c和a的值会被修改，并且程序运行结束的时候会让你关闭程序。

 

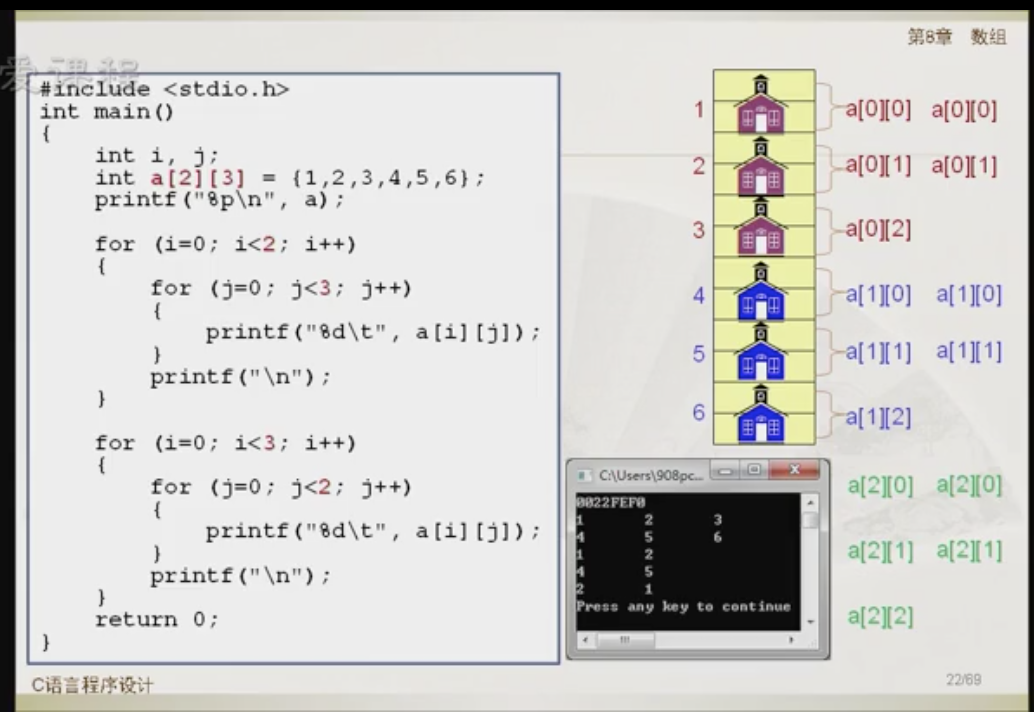
二维数组的定义和初始化

二维数组逻辑上是有行有列的，在内存当中，仍然是线性存储的。n维数组需要n个下标确定元素在数组中的位置。

 

存放顺序：按行存放，线性存储。先顺序存放第0行，再第1行...

二维数组初始化的时候，第二维的大小不能省略，列数一定要指定，因为是按行存的。

 

二维数组的下标越界会出现什么情况？后果也很严重！

 

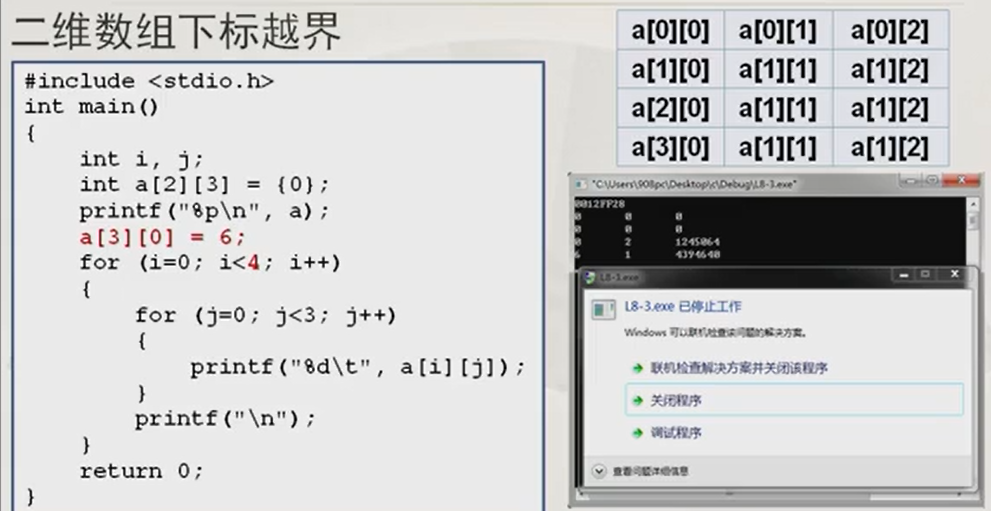
修改一下程序，下标越界后修改了数组中的值a[1][0]

 

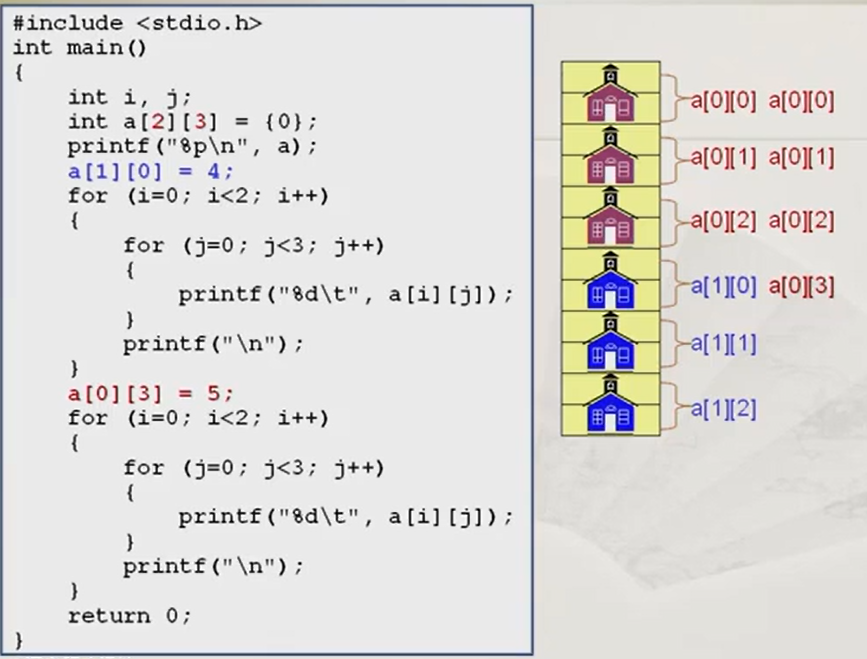
再修改一下，第一次输出3行2列，第二次输出2行3列，会出现什么结果？

 

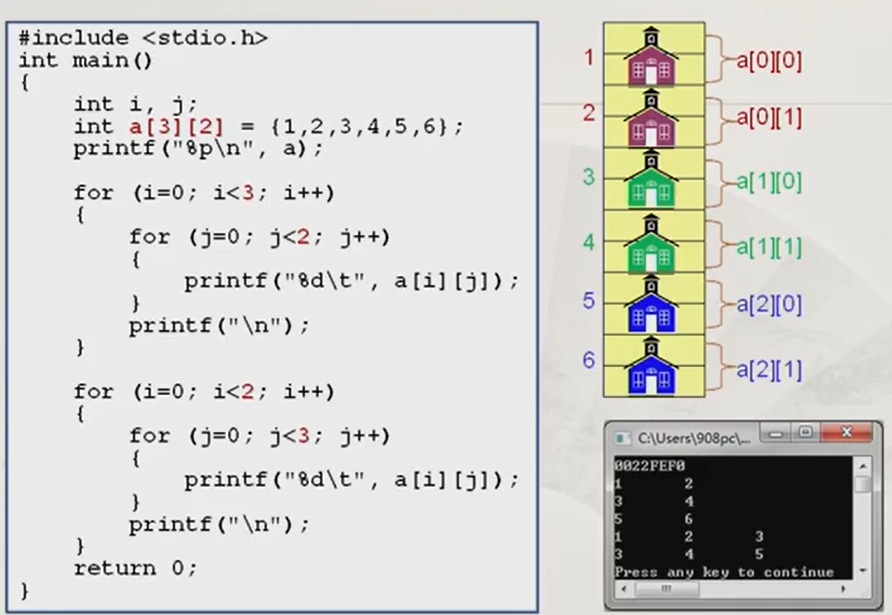
再把程序修改一下  ：a[3][2]改为a[2][3]，然后按照3行2列输出

 

 例：从键盘输入某年某月（包括闰年），编程输出该年的该月拥有的天数

 

如何向函数传递一维数组，就是将数组作为函数参数？

数组作为函数参数，按地址调用；传递数组的首地址，实参与形参数组占同一段内存单元

普通变量作函数参数，按值调用；传递变量值的副本，实参与形参变量占不同的内存单元。

 

传递数组首地址，效率更高。

 

例1：计算平均分：计数控制-键盘输入学生人数

例2：计算平均数：标记控制-负值作为输入结束标记

例3：计算最高分 int score[5] = {84, 83, 88 ,87 ,61]

返回最高分的数组下标

 int FindMaxNum(int Score[], int n){
       int i,maxNum;
       maxNum = 0;
       for(i=1; i<n; i++){
           if(Score[i] > Score[maxNum]){
               maxNum = i;
           }
      }
      return maxNum;
  }

 

排序和查找是常用的操作

    比如，对扑克牌进行排序；青年歌手大奖赛成绩排名；从图书馆的书架上查找某一本书；

　　百度、谷歌等网站搜索

 

排序算法

交换排序、选择排序、冒泡排序、插入排序、快速排序 

 

1、交换法排序

n个数需要n-1次比较

例：使用交换法对成绩降序排序

借助中间变量实现两数交换

for ( i=0; i<n-1; i++){
    for(j=i+1; j<n; j++){
        if(score[i] < score[j]){
            temp = score[i];
            socre[i] = score[j];
            score[j] = temp;
        }
    }
}

 

不借助中间变量完成两数交换,这种方法不安全并且可读性不高。加法可能会产生溢出，除法可能除数为0，此类方法不如有中间变量的交换

a = a+b;

b = a-b;

a = a-b;

或者

b = a*b

a = b/a

b = b/a

 

2、选择排序

选择一个最高的，记住其下标位置 

升序还是降序看大于号还是小于号；

按照成绩降序排序：

for ( i=0; i<n-1; i++){
    k = i;
    for( j = i+1; j<n; j++){
        if(score[j] > score[k]){
            k = j;
        }
    }
    if (k!= i){
        temp = score[k];
        score[k] = score[i];
        score[i] = temp;

        temp2 = num[k];
        num[k] = num[i]
        num[i] = temp2;
    }

数组越界：

例如 int a[2][3];

a[0][3] 的值其实就是a[1][0],这种越界虽然不会会带来隐患。

 

选择排序的效率比交换要高

 

查找算法

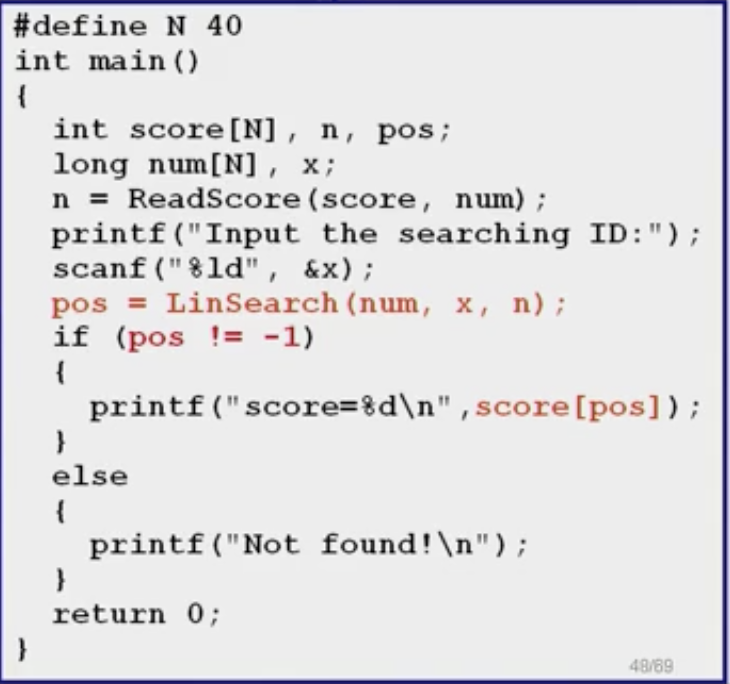
1、顺序查找

事先不必排序，考虑最坏情况的话，查找次数等于数据量大小，效率低下

找到返回该值，找不到返回-1。

   int LinSearch(long num[], long x, int n){
       int i;
       for(i=0;i<n;i++){
           if(num[i] == x){
               return i;
           }
      }
      return -1;
  }

例：顺序查找某学号对应的学生的成绩

 

猜数游戏解决问题的方法：找中间数猜

2、二分查找（折半查找）

1024个查找需要10次，即2的幂次方。

折半查找首先要进行排序，找到的情况：

 

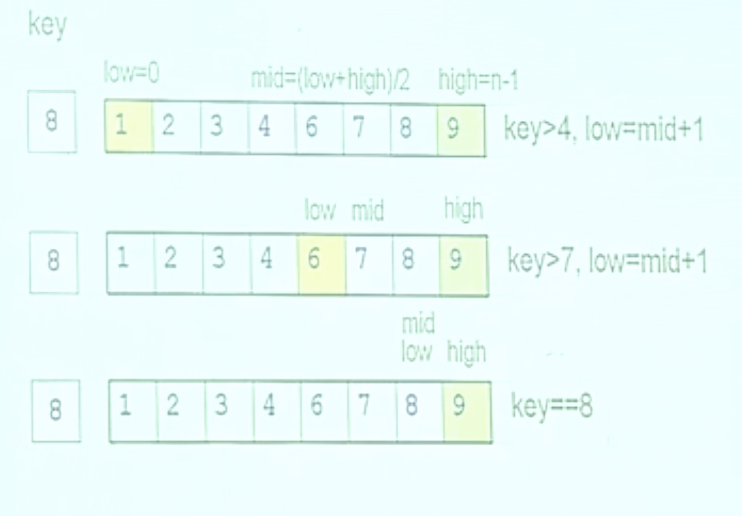
什么情况下没找到呢？ low>high

例：折半查找算法：

int BinSearch(long num[] ,long x, int n){
    int low,high,mid;
    low =0;
    high = n-1;
    while(low<=high){
        mid = (high+low)/2;
        if(x > num[mid]){
            low = mid+1;
        }
        else if(x < num[mid]){
            high = mid-1;
        }
        else{
            return mid;
        }
    }
    return -1;
}

如果这个数组很大，high和low都很大的时候，数组下标mid可能会溢出，使mid成为一个负数。

防止溢出的解决办法：修改计算中间值的方法，用减法代替加法

mid = low + (high-low)/2

我们这一章很大程度上都在讲安全性，safety（程序内部的安全） security(抵御外部入侵）

 

向函数传递二维数组

在声明函数的二维数组形参时，为什么不能省略数组第二维的长度？

元素a[i][j]在数组中相对于第一个元素的位置：

　　i*第二维长度+j

元素地址：首地址+偏移量

实际的地址：首地址+偏移量*每个数组元素所占的内存字节数（sizeof(short)）

 

数组的应用

1、保存n个学生一门课程的成绩，用一维数组

int Average(int score[],int n);

通常不指定数组的长度，用另一个形参来指定数组的大小

2、保存n个学生m门课程的成绩

用二维数组

void Average(int score[][COURSE_N], float aver[],int n);

可以省略数组第一维的长度，不能省略第二维的长度

数组aver可保存每个学生的平均分，或每门课程的平均分

 

例：计算每个学生的总分和平均分

void AverforStud(int score[][COURSE_N], int sum[],float aver[], int n){
    int i,j;
    for(i = 0; i<n; i++){//先遍历每个学生
        sum[i] = 0
        for(j=0; j<COURSE_N; j++){//遍历每门课程
            sum[i] = sum[i] + score[i][j];
        }
        aver[i] = (float) sum[i]/COURSE_N;
    }
}

如何计算每门课程的总分和平均分：先遍历每门课，再遍历每个学生

 

数组的其他应用

1、如何判断一个整数x是否是素数

不能被1和x以外的其他整数的正整数

试商法，用2~x-1之间的整数去试商看能否整除

用2~sqrt(x)之间的整数去试商看能否被整除即可。

int IsPrime(int x){
    int i,flag = 1;
    int squareRoot = sqrt(x);
    if(x<=1) flag = 0;
    for(i = 2; i<=squareRoot && flag;i++){
        if(x%i == 0) flag = 0;
    }
    return flag;
}

 

求100以内的所有素数，可以将上面的程序循环100次，但是效率低下。

使用筛法求100以内的所有素数（排除法）

依次从数组a中筛选2的倍数，3的倍数，5的倍数，7的倍数...

自顶向下，逐步求精设计算法

1：设计总体算法

　　初始化数组a，使a[2]=2,a[3]=3,...a[N]=[N]

　　对i=2,3.....sqrt(N)分别做“筛掉a中所有a[i]的倍数”

　　输出数组中余下的数(a[i]!=0的数）

2：对“筛掉a中所有的a[i]的倍数”求精

　　对数组a中的下标i后j对应所有的数分别做：

　　若“改数a[j]是a[i]的倍数”，则“筛掉该数a[j]”

3：对若“该数a[j]是a[i]的倍数”，则“筛掉该数a[j]"求精

if(a[i]!=0 && a[j]!=0 && a[j]%a[i] == 0){
    a[j] = 0;        
}

 

整个程序：

int i,j,a[N+1]
for( i=2; i<=N; i++){
    a[i] = i;
}

for(i = 2; i<=sqrt(N); i++){
    for(j = i+1; j<=N; j++){
        if(a[i]!=0 && a[j]!= 0 && a[j]%a[i]==0 ){
            a[j] = 0;
        }
    }
}

 

筛法用在其他问题上：

1、鲁智深吃馒头

据说，鲁智深一天中午匆匆来到开封府大相国寺，想蹭顿饭吃，当时大相国寺有99个和尚，只做了99个馒头。智清长老不愿得罪鲁智深，便把他安排在一个特定位置，之后对所有人说：从我开始报数（围成一圈），第5个人可以吃到馒头（并退下）

按此方法，所有和尚都吃到了馒头，唯独鲁智深没有吃上，请问他在什么位置？借鉴筛法求出剩下的最后一个人的位置

2、50位的n!计算？

为什么结果会这样？小数点16位之后都是0.

实数是按阶码和尾数来存储的，存在精度问题，double类型精度32位，但是表示范围就小了。

挑战类型表示的极限-大数存储的问题，用数组的每个元素来存储每一位，并且实现自动进位

 

小结

如何定义数组

如何向函数传递一位数组

　　传递数组的首地址，形参数组和实参数组共享同一段内存

　　通常不指定数组的长度，用另一个形参来指定数组的大小

如何向函数传递二维数组

　　可省略数组第一维的长度，不能省略第二维的长度

常用算法：排序、查找、求最值