Codeforces Round 960 (Div. 2) A - D

link

好图好图 qwq

这次也是终于装上插件 codeforces better! 了，妈妈再也不用担心我的英语啦

---

A - Submission Bait

A 先手，B 后手，优先往奇偶性的方向想

一开始我只是单纯考虑 A 总是选最大值的数的奇偶性，样例过了？交上去发现 wa 2

然后恼 ... 瞎搞了个 3 3 3 4 4，发现 A 可以先选 3 则必赢，

咦？如果所有偶数位都只能按照 B -> A，B -> A ... 这样后手一定在 A 上，则 A 必赢

考虑从大到小，有多个 ai 是偶数个，aj 为 第一个 是奇数个的数，那么走一次 aj，B 就只能往更大的数走，但是更大的数都是偶数个，这样就必赢

也就是说，只要有这个 aj 存在就一定能赢，所以，这题的结论就是判断是否（一开始我有考虑多个奇数个数是否影响结论，但这显然不会，因为 A 可以总是选最大的那个，也就是 aj，这样比它小的就没吊用）有奇数个的数即可

code

#include <bits/stdc++.h>
#define re register int 

using namespace std;
const int N = 100;

int T, n, a[N], bucket[N];

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> T;
	while (T --)
	{
		cin >> n;
		
		for (re i = 1; i <= N; i ++) bucket[i] = 0;
		
		for (re i = 1; i <= n; i ++)
		{
			cin >> a[i];
			bucket[a[i]] ++;
		}
		int ji = 0, ou = 0;
		for (re i = 1; i <= N; i ++)
		{
			if (bucket[i] == 0) continue;
			if (bucket[i] % 2 == 0) ou ++;
			else
			{
				ji ++;
			}
		}
		
		cout << (ji ? "Yes" : "No") << '\n';
	}
	
	return 0;
}

---

B - Array Craft

烦死了这题，没看到 y < x，一直按照 1 ≤ x < y ≤ n 做就不知道为什么一直 wa，要认真审题呀！

构造题

题意就是要构造两个函数，

使 prefix 的最大值区间左界为 x，suffix 的最大值区间右界在 y

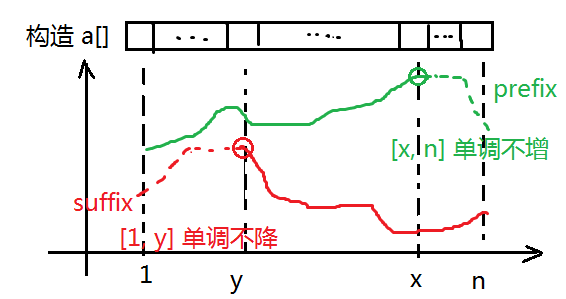
构造的话，就很显然了

[1, y) 和 (x, n] 可以直接弱化为常数函数，也就是 1, -1, 1 ... 交替

中间一种可行的构造就是保证从左往右单调递增，从右往左也单调递增，那么 [y, x] 全部为 1

注意：在交界处，不能使两个 1 相邻，这样就会拓展出去，

所以必须是 ... 1, -1, 1(y), 1, ... 1, 1(x), -1, 1 ...

code

#include <bits/stdc++.h>
#define re register int 

using namespace std;
const int N = 1e5 + 10;

int T, n, x, y;

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> T;
	while (T --)
	{
		cin >> n >> x >> y;
		
		int l = y - 1, r = n - x;
		if (l % 2) 
			for (re i = 1; i <= y - 1; i ++) cout << (i % 2 ? -1 : 1) << ' ';
		else  
			for (re i = 1; i <= y - 1; i ++) cout << (i % 2 ? 1 : -1) << ' ';
		
		for (re i = y; i <= x; i ++) cout << 1 << ' ';
		
		for (re i = x + 1, p = 1; i <= n; i ++) cout << (p ++ % 2 ? -1 : 1) << ' ';
			
		cout << '\n';
	}
	
	return 0;
}

---

C - Mad MAD Sum

似乎就是简单枚举？那就摸几个样例看看性质

• 显然的，发现 \(\forall\) b[] ，数组中的数 从左往右是单调不降的

• 好像还有一种三角形性质？

不关心 a[]，它的贡献仅仅是一开始的累加 \(ans += \sum\limits_{i = 1}^{n}a_i\)，比如第一个 b[]：0 1 1 2 3 3 4 4 4

b1： 0 1 1 2 3 3 4 4 4
b2： 0 0 1 1 1 3 3 4 4
b3： 0 0 0 1 1 1 3 3 4
b4： 0 0 0 0 1 1 1 3 3
b5： 0 0 0 0 0 1 1 1 3
b6： 0 0 0 0 0 0 1 1 1
b7： 0 0 0 0 0 0 0 1 1
b8： 0 0 0 0 0 0 0 0 1
b9： 0 0 0 0 0 0 0 0 0

三角形这个性质好啊！发现这里的贡献可以分为两种：

• 一种是边界形似三角形的数，比如 1，它实际的贡献其实是不规则的，但因为单调不降的性质，我们可以先把它直接当做整个三角形累加，后边减去相应的数 pre 再累加贡献即可

• 一种是孤立的点，比如 2，那贡献就是它本身，注意也要减去 pre，但是注意，单点是不会传递为 pre 的

code

#include <bits/stdc++.h>
#define re register int 

using namespace std;
typedef long long LL;
const int N = 2e5 + 10;

int T, n, a[N], b[N];
LL ans;

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> T;
	while (T --)
	{
		cin >> n;
		int mx = 0, bucket[N];
		for (re i = 1; i <= N; i ++) bucket[i] = 0;
		ans = 0;
		
		for (re i = 1; i <= n; i ++)
		{
			cin >> a[i];
			bucket[a[i]] ++;
			ans += a[i];
			
			if (a[i] > mx && bucket[a[i]] >= 2) mx = a[i];
			b[i] = mx;
		}
	
		int pre = 0;
		for (re i = 1; i <= n; i ++)
		{
			if (b[i] == 0) continue;
			
			int j = i;
			while (j + 1 <= n && b[j + 1] == b[i]) j ++;
			
			if (j == i) ans += b[i] - pre;
			else
			{
				int len = n - i + 1;
				ans += (LL)(b[i] - pre) * (len + 1) * len / 2;
				pre = b[i];
			}
			
			i = j;
		}
		cout << ans << '\n';
	}
	
	return 0;
}

---

D - Grid Puzzle

咕咕咕

E1 - Catch the Mole(Easy Version)（交互题）

E2 - Catch the Mole(Hard Version)

F - Polygonal Segments