树论
树的重心
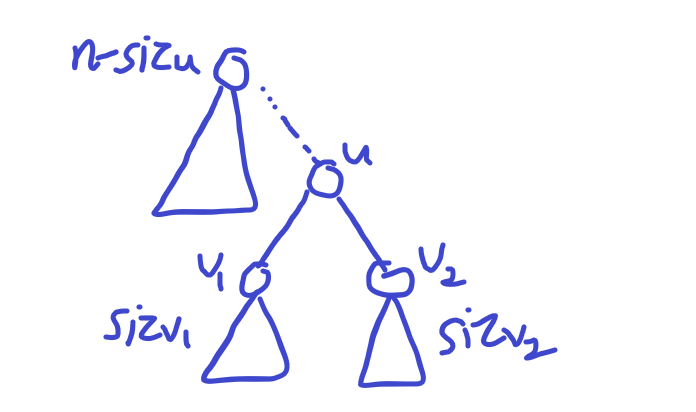
定义 max_part(u) 表示 max{n - siz[u], siz[v1], siz[v2]},表示对于当前点向三个方向上的最大子树大小
定义树的重心即为树中 max_part(u) 取得 最小 时的节点
很容易 dfs 得到树的重心
code
#include <bits/stdc++.h>
#define re register int
using namespace std;
const int N = 5e4 + 10, inf = 0x3f3f3f3f;
struct Edge
{
int to, next;
}e[N << 1];
int top, h[N];
int n, siz[N];
struct Node
{
int ans, id;
}a[N];
int cnt;
int res[N], idx;
bool cmp(Node i, Node j) { return i.ans < j.ans; }
inline void add(int x, int y)
{
e[++ top] = (Edge){y, h[x]};
h[x] = top;
}
void dfs(int u, int fa)
{
siz[u] = 1;
int max_part = 0;
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
dfs(v, u);
siz[u] += siz[v];
max_part = max(max_part, siz[v]);
}
max_part = max(max_part, n - siz[u]);
a[++ cnt] = (Node){max_part, u};
// cout << "id - max: " << u << ' ' << max_part << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for (re i = 1; i < n; i ++)
{
int x, y; cin >> x >> y;
add(x, y), add(y, x);
}
dfs(1, 0);
sort(a + 1, a + cnt + 1, cmp);
int mn = a[1].ans;
res[++ idx] = a[1].id;
for (re i = 2; i <= cnt; i ++)
{
if (a[i].ans > mn) break;
res[++ idx] = a[i].id;
}
sort(res + 1, res + idx + 1);
for (re i = 1; i <= idx; i ++) cout << res[i] << ' ';
return 0;
}
树的直径
树的直径就是树上最远两点间简单路径的距离,也就是树上最长的简单路径。
可以用 树形 dp 的思想做
考察树上任意节点 u,若它有 i 条子树,则就有 i 条过 u 点(严格是以 u 为端点)的路径,要找到 悬挂 在 u 点的最长路径,贪心地想就是找到 最长路径 和 次长路径 合起来就是过 u 点的可能解
设 d1,d2 分别表示最长路径,次长路径,边界肯定就是 0(直径只包含一个点)
对于 (u, v) 方向上的子树路径长度 d,可以递推求解
- d > d1,则 d2 = d1, d1 = d
- d > d2,则 d2 = d
结果就是对所有点的最长路径取最大值 \(\large\max\limits_{i\in V}\{d1_i + d2_i\}\),复杂度 \(O(n)\)
code
int dfs(int u, int fa)
{
int d1 = 0, d2 = 0;
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].w;
if (v == fa) continue;
int d = dfs(v, u) + w;
if (d > d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
res = max(res, d1 + d2);
return d1;
}
// 当然,如果要记录下来,也可以写成 dp 数组的形式
void dfs(int u, int fa)
{
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].w;
if (v == fa) continue;
dfs(v, u);
if (f[v][1] + w > f[u][1])
{
f[u][0] = f[u][1];
f[u][1] = f[v][1] + w;
}
else if (f[v][1] + w > f[u][0])
f[u][0] = f[v][1] + w;
}
len = max(len, f[u][1] + f[u][0]);
}
然鹅,dp 方法不好记录直径的路径
所以,有另一种方法,贪心两次 dfs,从任意点出发,dfs 到离它最远的点 p,再从 p dfs 到离它最远的点 q,则 p、q 一定是树上一条直径的两个端点。
但是,这种方法 不能处理含负边权的情况
证明
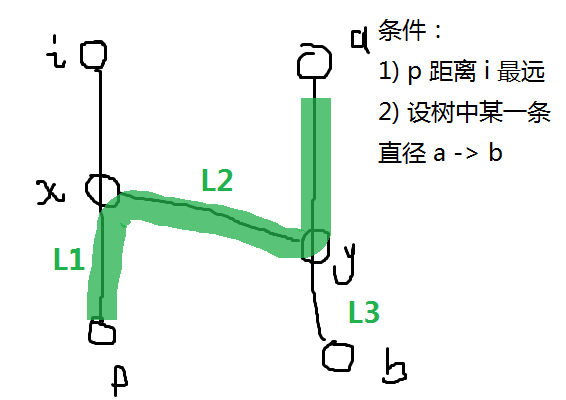
当然,这个证明也很简单,我也可以口胡一下。要证明 p -> q 是一条直径,因为 q 已经约束为离 p 最远的点,那么如果 p 是某条直径的端点,则必然有 q 是直径的端点,所以只需证明前者即可。
因为是一棵树,那么点之间必然可以互相到达,即有 i -> x -> y -> b
因为 p 距离 i 最远,则有 \(L_1 \geq L_2 + L_3\)
变形:\(L_1 - L_2 \geq L_3\)
当 \(L_1,L_2,L_3\in [0,+\infty)\),有 \(L_1+L_2\geq L_1 - L_2 \geq L_3\)那么 a -> p 的长度肯定是不短于直径 a -> b 的,
所以 a -> p 也是直径,p 也就是直径的端点。(同时证明中的约束条件也反映出这种做法在有负边权时是无效的)
code
int maxs = 0;
void dfs(int u, int fa, int size, int & to, int & res, int type)
{
if (size > maxs)
{
maxs = size;
to = u;
if (type) res = size; //type 区分 1 -> p 或 p -> q
}
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
if (type) pre[v] = u;
dfs(v, u, size + e[i].w, to, res, type);
}
}
直径中点 trick
性质:
在森林中,对两颗树分别连直径的中点,得到的新直径 \(\large\lceil \frac{d_i}{2} \rceil + \lceil \frac{d_j}{2} \rceil + w_k\) 一定是所有连接方案中最短的
这是显然的,要尽可能使原子树的直径均分,差值最小。
注意: 这个性质是普适的,但给出的代数式有局限的,只满足当树的边权都为 1 时,因为当边权不为 1 时,代数求得中点并不一定有对应的实际的点
练习:
P3761 [TJOI2017] 城市(这个题就是边权不为 1 要求树的半径,60pts 还没调出来)
很多时候,树的直径的题目没什么思考方向时,可以想一想如果找到了直径中点,有什么很好的东西
LCA
| 方法 | 预处理 | 查询 |
|---|---|---|
| 倍增法 | \(O(n\log n)\) | \(O(\log n)\) |
| 树链剖分 | \(O(n)\) | \(O(\log n)\)(任意一条路径不会被切分为超过 \(\log n\) 条链) |
| 欧拉序转化成 rmq 问题(结合 st 表) | \(O(n\log n)\) | \(O(1)\) |
(注意,虽然树剖查询的理论复杂度跟倍增法一样,但常数小很多,所有实际跑起来会更快,比如在模板题上,倍增法跑完大数据要 880ms±,而树剖是 360ms±)
倍增法
#include <bits/stdc++.h>
#define re register int
using namespace std;
const int N = 5e5 + 10, logN = 50;
struct Edge
{
int to, next;
}e[N << 1];
int top, h[N];
int n, q, s, dep[N], f[N][logN], lg[N];
inline void add(int x, int y)
{
e[++ top] = (Edge){y, h[x]};
h[x] = top;
}
void dfs(int u, int fa)
{
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for (re i = 1; i <= lg[n]; i ++)
f[u][i] = f[f[u][i - 1]][i - 1];
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
dfs(v, u);
}
}
inline int lca(int x, int y)
{
if (dep[x] < dep[y]) swap(x, y);
for (re i = lg[n]; i >= 0; i --)
if (dep[f[x][i]] >= dep[y]) x = f[x][i];
if (x == y) return x;
for (re i = lg[n]; i >= 0; i --)
if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> q >> s;
for (re i = 1; i < n; i ++)
{
int x, y; cin >> x >> y;
add(x, y), add(y, x);
}
lg[0] = -1;
for (re i = 1; i <= n; i ++) lg[i] = lg[i / 2] + 1;
dfs(s, 0);
while (q --)
{
int x, y; cin >> x >> y;
cout << lca(x, y) << '\n';
}
return 0;
}
树链剖分
#include <bits/stdc++.h>
#define re register int
using namespace std;
const int N = 5e5 + 10;
struct Edge
{
int to, next;
}e[N << 1];
int idx, h[N];
int fa[N], son[N], top[N], dep[N], siz[N];
int n, q, s;
inline void add(int x, int y)
{
e[++ idx] = (Edge){y, h[x]};
h[x] = idx;
}
void dfs1(int u, int fu)
{
fa[u] = fu;
dep[u] = dep[fu] + 1;
siz[u] = 1;
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fu) continue;
dfs1(v, u);
siz[u] += siz[v];
if (siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int t)
{
top[u] = t;
if (!son[u]) return;
dfs2(son[u], t);
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline int lca(int u, int v)
{
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
return (dep[u] > dep[v] ? v : u);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> q >> s;
for (re i = 1; i < n; i ++)
{
int x, y; cin >> x >> y;
add(x, y), add(y, x);
}
dfs1(s, 0);
dfs2(s, s);
while (q --)
{
int x, y; cin >> x >> y;
cout << lca(x, y) << '\n';
}
return 0;
}
两简单路径相交(点)trick
命题:
在一棵树中,有两组端点 \((a, b),(c, d)\),即两条简单路径,两组端点的 lca 分别是 \(x, y~(x\not = y)\),
若两路径存在交点,则必然有 \(x\) 在 c - d 的路径上或 \(y\) 在 a - b 的路径上。
这里我用反证法证明
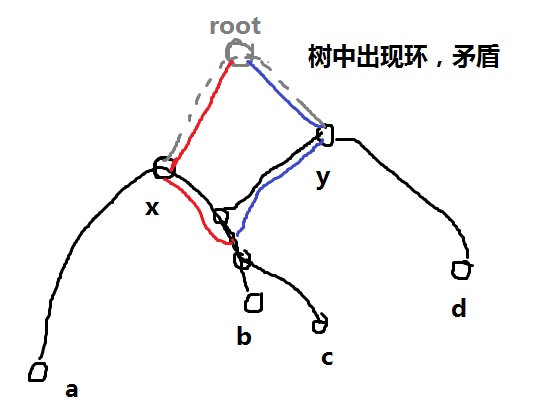
若交点集合不包括两 lca,我可以构造如下情况
x,y 到相交点集合中任意点存在不同路径,到根节点也存在不同路径,形成环路,矛盾
练习:
维护路径边权最值
很简单,倍增 lca 的同时再开个 st 表记录最值。
code
void dfs(int u, int fa)
{
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for (re i = 1; i <= log2(n); i ++)
{
f[u][i] = f[f[u][i - 1]][i - 1];
fw[u][i] = max(fw[u][i - 1], fw[f[u][i - 1]][i - 1]);
}
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].w;
if (v == fa) continue;
fw[v][0] = w;
dfs(v, u);
}
}
inline int lca(int u, int v)
{
int res = 0;
if (dep[u] < dep[v]) swap(u, v);
for (re i = log2(n); i >= 0; i --)
if (dep[f[u][i]] >= dep[v])
{
res = max(res, fw[u][i]);
u = f[u][i];
}
if (u == v) return res;
for (re i = log2(n); i >= 0; i --)
if (f[u][i] != f[v][i])
{
res = max(res, max(fw[u][i], fw[v][i]));
u = f[u][i];
v = f[v][i];
}
return max(res, max(fw[u][0], fw[v][0]));
}
树链剖分
顺便写这好了
初学感觉 树链剖分 就是在树形结构上维护区间修改和区间查询(类似序列上的线段树)
一些注意点:
-
特别地,单个叶子节点也算作一条重链
-
整棵树会被完全剖分成若干条重链
-
每条重链的顶点一定是轻儿子
-
任意一条路径不会被切分为超过 \(\log n\) 条链
口胡证明:
对一条轻边 \(x - y(dep_x < dep_y)\),因为 \(y\) 是 \(x\) 的轻儿子,不妨设重儿子为 \(z\),则根据定义有 \(size_z\geq size_y\)
那么就有 \(size_x \geq size_y+size_z\geq 2size_y\)既然对于任意轻边有 \(size_x\geq size_y\),那么每次上跳经过一个轻边,子树大小就会变成原来的至少两倍
那么最多上跳的轻边为 \(\log n\) 条,同理,最多上跳的重边不超过 \(\log n\) 条
树链剖分,简而言之,就是将树分成一条条链,然后用数据结构去维护这些链,以支持树上两点间的各种询问操作。
树链剖分大约有三种,分别是重链剖分、长链剖分和实链剖分(Link Cut Tree)。其中的重链剖分最为常见,所以一般说树链剖分(简称树剖)就是指重链剖分。
例如如果要分别在树上支持以下两种操作:
- 在两点间的简单路径上每个点的权值 + k
很显然,我们可以通过树上点差分,找到 lca,\(O(\log n)\) 处理,dfs 一遍 \(O(n + m)\) 还原实现
- 求两点间的简单路径上的节点权值之和
也很显然,可以先 dfs一遍 \(O(n + m)\) 预处理出根节点到每个点的节点权值和 \(sum\),每次查询通过树上点前缀和 \(O(\log n)\) 找到 lca 求解
但是。。。
如果要同时在线支持两种操作呢?暴力结合这两种做法就是 \(O(q(2\log n + n + m))\),也就是 \(O(qn)\) 级别,无法接受
所以,
树链剖分就是将树分成不同的链,并再次对每条链的点重新编号,
使每条链的节点编号是连续的,这样就可以将每条链到线段树上去维护
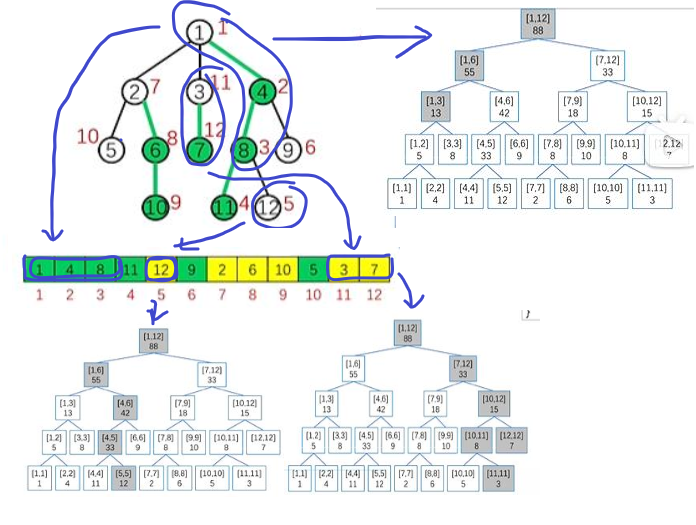
例如更新路径 7 - 12(这个图节点编号和权值相等),就分别上跳(类似),直至同一条链
树链剖分查询路径上覆盖的链需要 \(O(\log n)\),线段树对每条链更新、查询需要 \(O(\log n)\)
所以总的时间复杂度就是 \(O(q\log^2 n)\),非常优秀
code
#include <bits/stdc++.h>
#define re register int
#define lp p << 1
#define rp p << 1 | 1
using namespace std;
const int N = 1e5 + 10;
struct Edge
{
int to, next;
}e[N << 1];
int idx, h[N];
struct Tree
{
int l, r, sum, tag;
}t[N << 2];
int n, q, s, mod, a[N];
int fa[N], son[N], top[N], dep[N], siz[N];
int id[N], cnt, mat_w[N];
inline void add(int x, int y)
{
e[++ idx] = (Edge){y, h[x]};
h[x] = idx;
}
inline void push_up(int p)
{
t[p].sum = t[lp].sum + t[rp].sum;
}
inline void push_down(int p)
{
if (t[p].tag)
{
t[lp].sum += (t[lp].r - t[lp].l + 1) * t[p].tag;
t[rp].sum += (t[rp].r - t[rp].l + 1) * t[p].tag;
t[lp].tag += t[p].tag;
t[rp].tag += t[p].tag;
t[p].tag = 0;
}
}
void build(int p, int l, int r)
{
t[p].l = l, t[p].r = r;
if (l == r)
{
t[p].sum = mat_w[l];
return;
}
int mid = (l + r) >> 1;
build(lp, l, mid);
build(rp, mid + 1, r);
push_up(p);
}
inline void update(int p, int l, int r, int k)
{
if (l <= t[p].l && t[p].r <= r)
{
t[p].sum += (t[p].r - t[p].l + 1) * k;
t[p].tag += k;
return;
}
push_down(p);
int mid = (t[p].l + t[p].r) >> 1;
if (l <= mid) update(lp, l, r, k);
if (r > mid) update(rp, l, r, k);
push_up(p);
}
inline int query(int p, int l, int r)
{
if (l <= t[p].l && t[p].r <= r) return t[p].sum;
push_down(p);
int res = 0;
int mid = (t[p].l + t[p].r) >> 1;
if (l <= mid) res += query(lp, l, r) % mod;
if (r > mid) res += query(rp, l, r) % mod;
return res % mod;
}
void dfs(int u, int fu)
{
fa[u] = fu;
dep[u] = dep[fu] + 1;
siz[u] = 1;
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fu) continue;
dfs(v, u);
siz[u] += siz[v];
if (siz[son[u]] < siz[v]) son[u] = v;
}
}
void mark(int u, int t)
{
top[u] = t;
id[u] = ++ cnt;
mat_w[cnt] = a[u];
if (!son[u]) return;
mark(son[u], t);
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa[u] || v == son[u]) continue;
mark(v, v);
}
}
inline void update_path(int u, int v, int k)
{
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
update(1, id[top[u]], id[u], k);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
update(1, id[v], id[u], k);
}
inline int query_path(int u, int v)
{
int res = 0;
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res += query(1, id[top[u]], id[u]) % mod;
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res += query(1, id[v], id[u]) % mod;
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> q >> s >> mod;
for (re i = 1; i <= n; i ++) cin >> a[i];
for (re i = 1; i < n; i ++)
{
int x, y; cin >> x >> y;
add(x, y), add(y, x);
}
dfs(s, 0);
mark(s, s);
build(1, 1, n);
while (q --)
{
int op; cin >> op;
if (op == 1)
{
int x, y, z; cin >> x >> y >> z;
update_path(x, y, z);
}
if (op == 2)
{
int x, y; cin >> x >> y;
cout << query_path(x, y) % mod << '\n';
}
if (op == 3)
{
int x, z; cin >> x >> z;
update(1, id[x], id[x] + siz[x] - 1, z);
}
if (op == 4)
{
int x; cin >> x;
cout << query(1, id[x], id[x] + siz[x] - 1) % mod << '\n';
}
}
return 0;
}
写树剖这种代码量的算法,难调是真的,还是要细心
这里再记录一下我遇到的一些情况:
在某些树剖题中,有的出题人喜欢节点编号从 0 开始(
然后,你直接套板子上去,根节点从 0 开始,你就会发现 siz[0] = 1 !
这样的后果就是可能无法更新重儿子,从实际含义出发理解也可以,之前,根节点为 1 时,初始 son[1] = 0 为空,此时 siz[0] = 0,而现在 siz[0] = 1 就可能会导致 siz[son[u]] < siz[v] 不能成立,即有的重儿子没有被记录
重儿子少了,第二次搜索时连成的重边,重链就少了,上跳复杂度就从 \(O(\log n)\) 退化到 \(O(n)\)
基环树
n 个点,n 条边的图,也就是树上加一条边有且仅有一个环
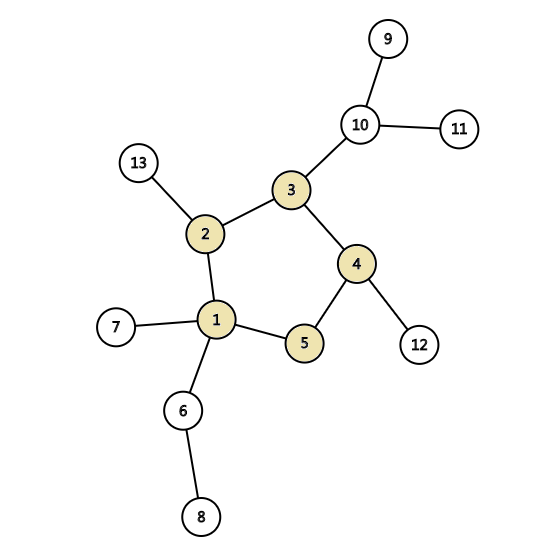
基环树(也称环套树)分三类
无向基环树,内向树、外向树(有向图中)
首先基环树最主要的特征,就是环,所有先要找到环
显然地,把无向边看作双向边,我们可以用拓扑排序 \(O(n)\) 找环,内向树也同样直接处理
外向树呢,我没有想到直接的处理办法,但是可以将它的所有边换向,转化为内向树处理,同样可以记录环,topsort 完后还原即可
code
inline void topsort()
{
queue<int> q;
for (re i = 1; i <= n; i ++)
if (in[i] == 1) q.push(i); // in[i] == 0 (有向图)
while (!q.empty())
{
int x = q.front(); q.pop();
for (re i = h[x]; i; i = e[i].next)
{
int y = e[i].to;
if (-- in[y] == 1) q.push(y); // in[i] == 0
}
}
for (re i = 1; i <= n; i ++)
if (in[i] == 2) ans[++ cnt] = i; // in[i] == 1
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号