前缀和 和 差分 思想的一些运用

前缀和

前缀和的基本模型是：

\(\large{sum_i = \sum\limits_{j=1}^i a_j}~, ~i\in(1,n)\)

若要对 \(a\) 的 \([l,r]\) 查询区间和，等价于 \(sum_r - sum_{l-1}\) .

---

树上前缀和

学树上差分顺便学了个前缀和...

点前缀和

路径 \(x\to y\) 的点权和为：

\[sum[x] + sum[y] - sum[~lca(x,y)~] - sum[~st[~lca(x,y),0]~] \]

边前缀和

路径 \(x\to y\) 的边权和为：

\[sum[x] + sum[y] - 2\times sum[~lca(x,y)~] \]

一切都是如此显然 qwq

• 题目

P8805 [蓝桥杯 2022 国 B] 机房

P4427 [BJOI2018] 求和

差分

差分的基本模型是：

\(\large{d_i = \begin{cases} a_i - a_{i-1} &,i\in[2,n] \\a_1 &,i=1 \end{cases}}\)

若要对 \(a\) 的 \([l, r]\) 区间进行在线区间修改，等价于 \(d_l + k,~d_{r+1} - k\) .

最后离线用前缀和还原结果：\(a_i = \sum\limits_{j=1}^{i}d_j\) ，\(tot = \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{i}d_j =\sum\limits_{i=1}^n (n-i+1)\cdot d_i\) .

---

树上差分

然鹅，这次要重点记录的是 树上差分（学了lca才发现有这玩意），分两种：树上点差分，树上边差分。

先讨论初始值为 0 的情况。

点差分

类似地，假如在一棵树上要对 \(x\to y\) 的唯一路径上的所有点 +1，可以定义一个差分数组 \(d\)，则：

\[d[x] + 1,~d[y] + 1,~d[~lca(x,y)~] -1,~d[~st[~lca(x,y),0]~] - 1 \]

在深搜回溯时累加儿子差值还原，可以发现，\(lca(x,y)\) 被访问了两次， 所以要在上面多 -1，其余和模型同理。

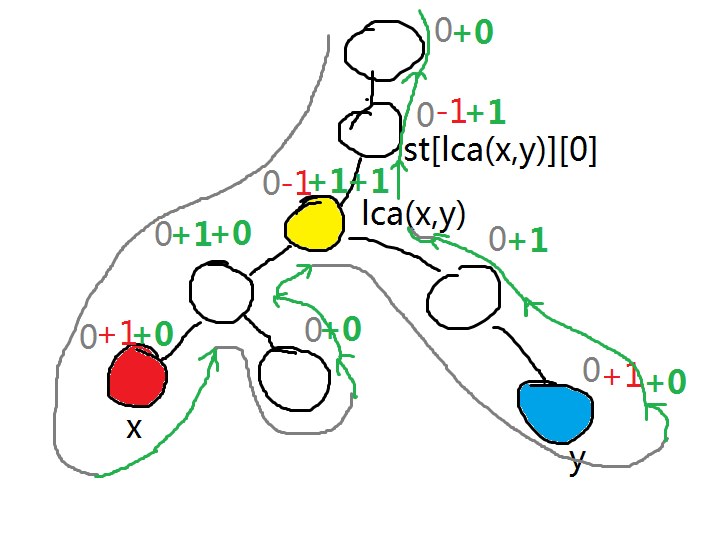
边差分

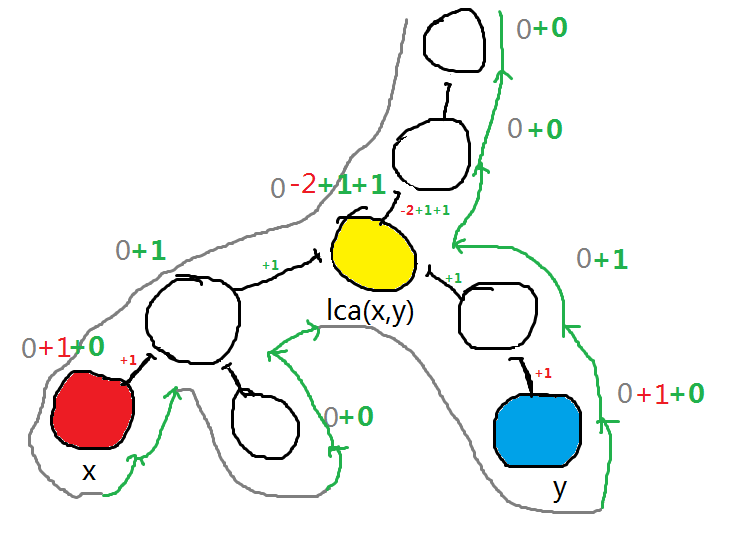
边不好直接处理，但是在树上有个特别的性质，若不看根节点，其余每个点都有一条唯一的边与之对应，这样就巧妙地用点来处理边的信息，则：

\[d[x] + 1,~d[y] + 1,~d[~lca(x,y)~] - 2 \]

从图中可以看到，\(lca(x,y)\) 的点被访问了两次，而其实与之相关的边不在 \(x\to y\) 的路径上，直接减掉就可以。

在此基础上，讨论初始值不为 0 的情况。

其实就是在维护前，预处理出每个点 / 每条边的差分值，与模型同理。

具体地，叶子节点的差分值就是它本身，其余节点的差分值 = 该点值 - 所有儿子的值。

回溯还原时，该点值 = 所有儿子的值 + 该点差分值。边的处理同边差分同理（一堆废话）

• 题目

P3128 [USACO15DEC] Max Flow P

P3258 [JLOI2014] 松鼠的新家

P2680 [NOIP2015 提高组] 运输计划