并查集笔记

原理

在线维护集合的合并和查询

int find(int x)
{
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

时间复杂度

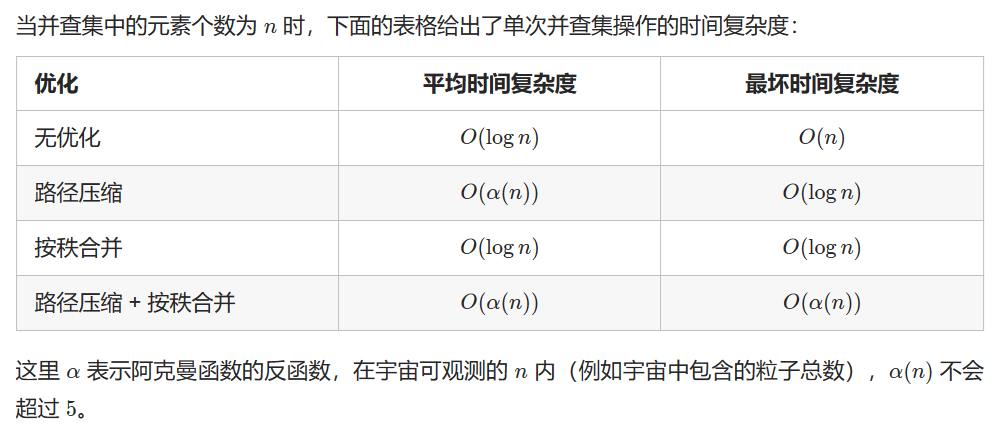
运用

题单

1. P6121 [USACO16OPEN] Closing the Farm G

P3144 [USACO16OPEN] Closing the Farm S（逊版）

思路 \(\scr{Solution}\)

\(10pts\)

每一时刻关闭农场，求是否全联通。也就是维护将单个集合分成多个集合。

很容易想到爆搜算法，用 vector 邻接表建图，每次跑完图就将当前点的连边关系删去。复杂度 \(O(n^2)\)

只能拿 10pts ，居然有 WA qwq

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10;
int n, m;
bool vis[N];
vector<int> g[N];

void dfs(int fa, int x)
{
	for (int i = 0; i < g[x].size(); i ++)
	{
		int y = g[x][i];
		if (y == fa || vis[y]) continue;
		vis[y] = true;
		dfs(x, y);
	}
}

void cut(int x)
{
	for (int i = 0; i <g[x].size(); i ++)
		g[x][i] = -1;
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i ++)
	{
		int x, y;
		cin >> x >> y;
		g[x].push_back(y);
		g[y].push_back(x);
	}
	while (n --)
	{
		memset(vis, false, sizeof(vis));
		int x;
		cin >> x;
		vis[x] = true;
		dfs(0, x);
		bool flag = false;
		for (int i = 1; i <= n; i ++)
			if (!vis[i])
			{
				flag = true;
				break;
			}
		cout << (flag ? "NO" : "YES") << '\n';
		cut(x);
	}
	
	return 0;
}

正着搜不好优化，考虑倒过来思考。

即一开始所有农场都是关闭的，从后往前，判断每一时刻打开一个农场，对应正着想的当前状态下该农场还未关闭。

而正着想是判断当前状态下是否因关闭该农场而被分成了多个集合。

那倒着想就是打开多个农场，判断是否有多个集合（连通块）！

这不就是并查集了吗 ......

每次打开一个农场，默认多了一个集合，再通过图遍历直接相连的点是否打开了，打开了但又不在同一集合里就用并查集合并，同时抹去该单点集合。

每次操作完后就留下了当前状态下打开了的相连农场的集合数量。

\(O(m)~\) done.

#include<bits/stdc++.h>
using namespace std;
const int N =  2e5 + 10;
int n, m, a[N], fa[N], ans[N];
bool vis[N];
vector<int> g[N];

int find(int x)
{
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i ++)
	{
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for (int i = 1; i <= n; i ++) cin >> a[i];
	for (int i = 1; i <= n; i ++) fa[i] = i;
	int sum = 0;
	for (int i = n; i >= 1; i --)
	{
		sum ++;
		int k = a[i];
		vis[k] = true;
		for (int j = 0; j < g[k].size(); j ++)
		{
			int l = g[k][j];
			if (find(k) != find(l) && vis[l])
			{
				merge(k, l);
				sum --;
			}
		}
		ans[i] = sum;
	}
	for (int i = 1; i <= n; i ++)
		cout << (ans[i] == 1 ? "YES" : "NO") << '\n';
		
 	return 0;
}

总结 \(\scr{Summary}\)

有些题目正着想好做但常常不够优，所以当发现正着想超时时可以试着倒着思考；
一些删边的问题可以转化为加边的问题来做，从而考虑并查集；

类似思想的题

2. P7991 [USACO21DEC] Connecting Two Barns S

思路 \(\scr{Solution}\)

\(50pts\)

相当于从 \(1\sim n\) 的一条通路被分成了多条断路，再将它们之间互相连接求最小费用。

可以用并查集维护集合关系，而至多可以连两条路就可以分成三种情况：

0 条，说明 1 和 n 已经连通，费用为 0；
1 条，将 1 和 n 所在集合直接连一条最小边；
2 条，选一个第三方集合作为桥，分别连接两条最小边；

易想到枚举所有其他集合再和 1、n所在集合暴力枚举打擂台，复杂度为 \(O(n^2)\)，只能拿 50pts

点击查看代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 2e5 + 10, inf = LONG_LONG_MAX;
ll t, n, m, fa[N];
vector<ll> a[N];

void init()
{
	for (int i = 1; i <= n; i ++)
	{
		fa[i] = i;
		a[i].clear();
	}
}

ll find(int x)
{
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

ll count(int x, int y)
{
	ll ans = inf;
	for (int i = 0; i < a[x].size(); i ++)
		for (int j = 0; j < a[y].size(); j ++)
		{
			ll k = a[x][i], l = a[y][j];
			ans = min(ans, (k - l) * (k - l));
		}	
	return ans;		
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> t;
	while (t --)
	{
		cin >> n >> m;
		init();
		for (int i = 1; i <= m; i ++)
		{
			int x, y;
			cin >> x >> y;
			merge(x, y);
		}
		for (int i = 1; i <= n; i ++) a[find(i)].push_back(i);
		if (find(1) == find(n)) 
		{
			cout << 0 << '\n';
			continue;
		}
		ll ans = inf;
		for (int i = 1; i <= n; i ++)
		{
			if (find(i) == find(1) || find(i) == find(n) || find(i) != i) continue;
			ans = min(ans, count(find(i), find(1)) + count(find(i), find(n)));
		}
		cout << min(ans, count(find(1), find(n))) << '\n';
	}
	
	return 0;
}

显然是暴力枚举这还可以优化，而回想打擂台的目的是在1、n所在集合里找到与第三方集合里两两最近的点。

保留任意一个集合枚举，那另一个要找到与当前集合的点最近的点。

考虑 二分查找优化

此时就要求维护集合并且集合内有序，可以考虑用 set 实现。

不想手打二分（悲，所以用 .lower_bound(x) 函数可以直接查找第一个 \(\geqslant x\) 的数的地址。

但 set 没有查找第一个 \(< x\) 的函数，所以考虑在1、n所在集合 \(A\) 有 \(A_{i-1} < x \leqslant A_i\)，且集合大小为 \(n_A\)，设 \(x_j \in B\)，且大小为 \(n_B\)

易得：

\[ans = \min\limits_{j\in[1,n_{B}~]} \begin{cases} (A_i-x_j)^2&(i\in[1,n_A]) \\ (A_{i-1}-x_j)^2&(i \not\in[1,n_A]~||~i>1) \end{cases} \]

\(O(n\log \sqrt{n})~\) done.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 2e5 + 10, inf = LONG_LONG_MAX;
ll t, n, m, fa[N];
set<ll> s[N];

void init()
{
	for (int i = 1; i <= n; i ++)
	{
		fa[i] = i;
		s[i].clear();
	}
}

ll find(int x)
{
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

ll count(int x, int y)
{
	ll ans = inf;
	set<ll>::iterator i, j;
	for (i = s[x].begin(); i != s[x].end(); i ++)
	{
		j = s[y].lower_bound(*i);
		if (j != s[y].end()) ans = min(ans, (*j - *i) * (*j - *i));
		if (j == s[y].end() || j != s[y].begin()) ans = min(ans, (*(-- j) - *i) * (*j - *i));
	}
	return ans;		
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> t;
	while (t --)
	{
		cin >> n >> m;
		init();
		for (int i = 1; i <= m; i ++)
		{
			int x, y;
			cin >> x >> y;
			merge(x, y);
		}
		for (int i = 1; i <= n; i ++) s[find(i)].insert(i);
		if (find(1) == find(n)) 
		{
			cout << 0 << '\n';
			continue;
		}
		ll ans = inf;
		for (int i = 1; i <= n; i ++)
		{
			if (find(i) == find(1) || find(i) == find(n) || find(i) != i) continue;
			ans = min(ans, count(find(i), find(1)) + count(find(i), find(n)));
		}
		cout << min(ans, count(find(1), find(n))) << '\n';
	}
	
	return 0;
}

总结 \(\scr{Summary}\)

要熟知 STL 常用容器的特性，不仅可以简化思路，有时可以通过特性找到解题、优化思路；

3. P1840 Color the Axis

思路 \(\scr{Solution}\)

最先想到的肯定是直接模拟染色过程，每次暴力查找，时间为 \(O(nm)\)，直接 T 飞。

然鹅，当范围 \([l,r]\) 里的点都被染成黑色时，完全可以把这个集合看做一个点来进行下一次染色，这样大大压缩查找时间。

想到用并查集维护。

具体地，在下一次染色时该次染色就等价于压缩成点。

而每次查找从左到右，就可以把 \([l,r]\) 的点一一都合并到 \(r\) 作为根的集合，同时记录剩余点数。

注意：可能 \(r = n\)，此时会越界到 \(n+1\) !

\(O(n+m)~\) done.

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, fa[N];

int find(int x)
{
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> n >> m;
	int res = n;
	for (int i = 1; i <= n + 1; i ++) fa[i] = i;
	for (int i = 1; i <= m; i ++)
	{
		int l, r;
		cin >> l >> r;
		int a = find(l);
		while (a <= r)
		{
			merge(a, a + 1);
			a = find(a);
			res --;
		}
		cout << res << '\n';
	}
	
	return 0;
}

总结 \(\scr{Summary}\)

注意越界问题啊啊啊！

类似思想的问题

posted @ 2023-07-31 22:01 Zhang_Wenjie 阅读(47) 评论(0) 收藏举报

刷新页面返回顶部

$\large{\cal{ZhangWenjie}}$

昔日龌龊不足夸，来日放荡思无涯。春风得意马蹄疾，一日看尽长安花。

并查集笔记

原理

运用

1. P6121 [USACO16OPEN] Closing the Farm G

思路 \(\scr{Solution}\)

\(10pts\)

总结 \(\scr{Summary}\)

2. P7991 [USACO21DEC] Connecting Two Barns S

思路 \(\scr{Solution}\)

\(50pts\)

总结 \(\scr{Summary}\)

3. P1840 Color the Axis

思路 \(\scr{Solution}\)

总结 \(\scr{Summary}\)

公告

$\large{\cal{ZhangWenjie}}$

昔日龌龊不足夸，来日放荡思无涯。 春风得意马蹄疾，一日看尽长安花。

并查集 笔记

原理

运用

1. P6121 [USACO16OPEN] Closing the Farm G

思路 \(\scr{Solution}\)

\(10pts\)

总结 \(\scr{Summary}\)

2. P7991 [USACO21DEC] Connecting Two Barns S

思路 \(\scr{Solution}\)

\(50pts\)

总结 \(\scr{Summary}\)

3. P1840 Color the Axis

思路 \(\scr{Solution}\)

总结 \(\scr{Summary}\)

公告

昔日龌龊不足夸，来日放荡思无涯。春风得意马蹄疾，一日看尽长安花。

并查集笔记