221. Maximal Square

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example:

Input: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Output: 4

class Solution {
    public int maximalSquare(char[][] matrix) {
        int r = matrix.length;
        int c = r > 0 ? matrix[0].length : 0; 
        if(r == 0 || c == 0) return 0;
        int[][] dp = new int[r+1][c+1];
        int max = 0;
         
        for(int i = 1; i <= r; i++){
            for(int j = 1; j <= c; j++){
                if(matrix[i-1][j-1] == '1') dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i-1][j-1]), dp[i][j-1]) + 1;
                max = Math.max(max, dp[i][j]);
            }
        }

        return max * max;
    }
}

Algorithm

We will explain this approach with the help of an example.

0 1 1 1 0
1 1 1 1 1
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1

We initialize another matrix (dp) with the same dimensions as the original one initialized with all 0’s.

dp(i,j) represents the side length of the maximum square whose bottom right corner is the cell with index (i,j) in the original matrix.

Starting from index (0,0), for every 1 found in the original matrix, we update the value of the current element as

\text{dp}(i, j) = \min \big( \text{dp}(i-1, j), \text{dp}(i-1, j-1), \text{dp}(i, j-1) \big) + 1.dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1.

We also remember the size of the largest square found so far. In this way, we traverse the original matrix once and find out the required maximum size. This gives the side length of the square (say maxsqlenmaxsqlen). The required result is the area maxsqlen^2maxsqlen2.

To understand how this solution works, see the figure below.

An entry 2 at (1, 3)(1,3) implies that we have a square of side 2 up to that index in the original matrix. Similarly, a 2 at (1, 2)(1,2) and (2, 2)(2,2) implies that a square of side 2 exists up to that index in the original matrix. Now to make a square of side 3, only a single entry of 1 is pending at (2, 3)(2,3). So, we enter a 3 corresponding to that position in the dp array.

Now consider the case for the index (3, 4)(3,4). Here, the entries at index (3, 3)(3,3) and (2, 3)(2,3) imply that a square of side 3 is possible up to their indices. But, the entry 1 at index (2, 4)(2,4) indicates that a square of side 1 only can be formed up to its index. Therefore, while making an entry at the index (3, 4)(3,4), this element obstructs the formation of a square having a side larger than 2. Thus, the maximum sized square that can be formed up to this index is of size 2\times22×2.

干，这么巧妙。

想想大正方形怎么来的？从小正方形累积起来的。dp数组代表以该位置i j为右下角的正方形阶数，自然就得到了。

 

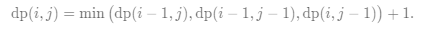
 注意判断空【】的情况，如果row==0就要立即返回，不能再用matrix[0].length表示col的length。