CSU-ACM2025 暑假集训 训练赛2 题解

A

U601940 公平组合游戏

题目很诈骗导致在结训赛落选......

题目名为公平组合游戏，实际上一点也不公平。

首先给出结论：\(Alice\) 先手必胜。

接下来进行证明：

当 \(n\) 为偶数时

第 \(n\) 个蛋糕一定谁也选不到，只有当只剩一个蛋糕时 \(Bob\) 轮空一次才能被 \(Alice\) 选到。所以第 \(n\) 个就是 \(Alice\) 的且不需要付出额外代价，所以可以归纳到 \(n\) 为奇数的情况。

当 \(n\) 为奇数时

令 \(x = \sum\limits_{i=2}^{n}[i\bmod 2=0] a_i\) , \(y = \sum\limits_{i=3}^{n}[i\bmod 2=1] a_i\)。

当 $ x \ge y $ 时

\(Alice\) 可以取 \(1\) 号位的蛋糕。此时后面的蛋糕奇偶颠倒，\(x \ge y\) 等价于此时奇数位之和大于等于偶数位之和。

当 $ x < y $ 时

\(Alice\) 可以取 \(n\) 号位的蛋糕。此时前面的蛋糕奇偶不变，\(x<y\) 等价于此时奇数位之和大于偶数位之和。

综上所述

\(Alice\) 总可以使得奇数位之和大于等于偶数位之和。此时 \(n\) 为偶数轮到 \(Bob\) 行动，当 \(Bob\) 取第 \(m\) 位时 \(Alice\) 总可以取 \(m-1\) 位使得其余所有蛋糕奇偶位不变。

综上

按照以上规则，\(Alice\) 总可以拿到 \(max(x,y)\), \(Bob\) 总是拿到 \(min(x,y)\) 。同时 \(Alice\) 总会多拿一个 \(a_1\)，当 \(n\) 为偶数时又会多拿一个 \(a_n\)， 所以 \(Alice\) 总是大于 \(Bob\)。

所以 \(Alice\) 先手必胜 。

std

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
void solve() {
	cout << "Alice" << endl;
}
signed main() {
	int t = 1;
	cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}

B

P4675 [BalticOI 2016] Park (day1) - 洛谷

经典 Trick :

我们发现不同的游客的大小不一样, 这很麻烦。

那么想办法, 把游客的大小转化成树的大小。

最显然的方法 , 就是对于每个半径为 \(r\) 的游客,让所有的树的半径加上 \(r\)。如图。

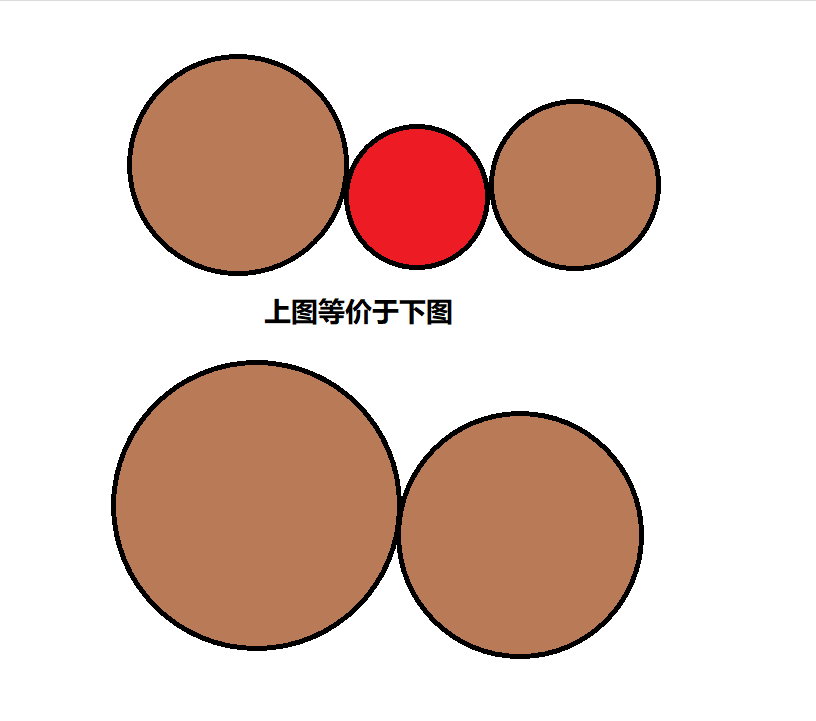
这样我们就可以把游客看做点了，这是后可以判段四个角之间是否联通，方法参考普及组难度题目《奶酪》，把四条边也都当作一个点。

当 \(A\) 与 \(B\) 不能联通有如下 \(3\) 种情况：

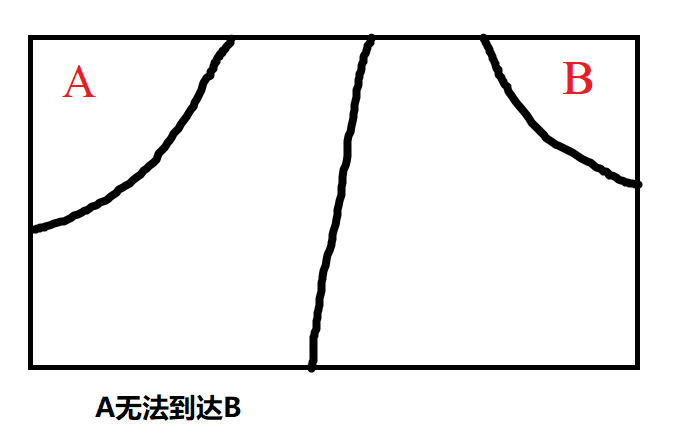
对于这道题,预处理出任意两棵树（包括边界）中间的路堵上所需的游客直径，拿一个指针扫描，然后判段连通性即可，注意根据题目，一个点总是可以到达其起点的。

std

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int  N = 1000005;
int f[N];
int ran[N];
void init(int n) {
	for (int i = 0; i <= n; i++) {
		f[i] = i;
		ran[i] = 1;
	}
}

int find(int x) {
	if (f[x] == x) return x;
	return f[x] = find(f[x]);
}

bool isSame(int x, int y) {
	return find(x) == find(y);
}

bool join(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y)
		return false;
	if (ran[x] > ran[y])
		f[y] = x;
	else {
		if (ran[x] == ran[y]) ran[y]++;
		f[x] = y;
	}
	return true;
}
long double dis[5][5];
signed main() {
	for (int i = 0; i <= 4; i++) {
		for (int j = 0; j <= 4; j++) {
			dis[i][j] = 1e18;
		}
	}
	int n, m;
	cin >> n >> m;
	int w, h;
	cin >> w >> h;
	init(n + 4);
	vector<pair<pair<int, int>, int>>z;
	vector<pair<long double, pair<int, int>>>e;
	for (int i = 1; i <= n; i++) {
		int x, y, r;
		cin >> x >> y >> r;
		int xx = 0;
		for (auto j : z) {
			xx++;
			e.push_back({ sqrtl((x - j.first.first) * (x - j.first.first) + (y - j.first.second) * (y - j.first.second)) - j.second - r, {i,xx} });
		}
		z.push_back({ {x,y},r });
		e.push_back({ x - (long double)r,{i,1 + n} });
		e.push_back({ y - (long double)r,{i,2 + n} });
		e.push_back({ w - x - (long double)r,{i,3 + n} });
		e.push_back({ h - y - (long double)r,{i,4 + n} });
	}
	sort(e.begin(), e.end());
	for (auto i : e) {
		join(i.second.first, i.second.second);
		if (isSame(n + 1, n + 2)) {
			dis[1][2] = min(dis[1][2], i.first);
			dis[2][1] = min(dis[2][1], i.first);
			dis[1][3] = min(dis[1][3], i.first);
			dis[3][1] = min(dis[3][1], i.first);
			dis[1][4] = min(dis[1][4], i.first);
			dis[4][1] = min(dis[4][1], i.first);
		}
		if (isSame(n + 1, n + 3)) {
			dis[1][3] = min(dis[1][3], i.first);
			dis[3][1] = min(dis[3][1], i.first);
			dis[1][4] = min(dis[1][4], i.first);
			dis[4][1] = min(dis[4][1], i.first);
			dis[2][3] = min(dis[2][3], i.first);
			dis[3][2] = min(dis[3][2], i.first);
			dis[2][4] = min(dis[2][4], i.first);
			dis[4][2] = min(dis[4][2], i.first);
		}
		if (isSame(n + 1, n + 4)) {
			dis[1][4] = min(dis[1][4], i.first);
			dis[4][1] = min(dis[4][1], i.first);
			dis[2][4] = min(dis[2][4], i.first);
			dis[4][2] = min(dis[4][2], i.first);
			dis[3][4] = min(dis[3][4], i.first);
			dis[4][3] = min(dis[4][3], i.first);
		}
		if (isSame(n + 2, n + 3)) {
			dis[2][3] = min(dis[2][3], i.first);
			dis[3][2] = min(dis[3][2], i.first);
			dis[2][4] = min(dis[2][4], i.first);
			dis[4][2] = min(dis[4][2], i.first);
			dis[1][2] = min(dis[1][2], i.first);
			dis[2][1] = min(dis[2][1], i.first);
		}
		if (isSame(n + 2, n + 4)) {
			dis[2][4] = min(dis[2][4], i.first);
			dis[4][2] = min(dis[4][2], i.first);
			dis[3][4] = min(dis[3][4], i.first);
			dis[4][3] = min(dis[4][3], i.first);
			dis[1][2] = min(dis[1][2], i.first);
			dis[2][1] = min(dis[2][1], i.first);
			dis[1][3] = min(dis[1][3], i.first);
			dis[3][1] = min(dis[3][1], i.first);
		}
		if (isSame(n + 3, n + 4)) {
			dis[3][4] = min(dis[3][4], i.first);
			dis[4][3] = min(dis[4][3], i.first);
			dis[2][3] = min(dis[2][3], i.first);
			dis[3][2] = min(dis[3][2], i.first);
			dis[1][3] = min(dis[1][3], i.first);
			dis[3][1] = min(dis[3][1], i.first);
		}
	}
	for (int i = 1; i <= m; i++) {
		int c, rr;
		cin >> rr >> c;
		rr *= 2;
		long double r = (long double)rr - 0.0001;
		if (c == 1) {
			cout << 1;
			if (dis[1][2] > r) {
				cout << 2;
			}
			if (dis[1][3] > r) {
				cout << 3;
			}
			if (dis[1][4] > r) {
				cout << 4;
			}
		}
		if (c == 2) {
			if (dis[2][1] > r) {
				cout << 1;
			}
			cout << 2;
			if (dis[2][3] > r) {
				cout << 3;
			}
			if (dis[2][4] > r) {
				cout << 4;
			}
		}
		if (c == 3) {
			if (dis[3][1] > r) {
				cout << 1;
			}
			if (dis[3][2] > r) {
				cout << 2;
			}
			cout << 3;
			if (dis[3][4] > r) {
				cout << 4;
			}
		}
		if (c == 4) {
			if (dis[4][1] > r) {
				cout << 1;
			}
			if (dis[4][2] > r) {
				cout << 2;
			}
			if (dis[4][3] > r) {
				cout << 3;
			}
			cout << 4;
		}
		cout << endl;
	}
	return 0;
}

C

P13105 [GCJ 2019 Qualification] Dat Bae - 洛谷

妙妙交互题。

感觉这种题没有什么通用技巧啊，只能依题目而定。

---

先考虑 \(F = 10\)。

看到 \(N \le 1024\) 即 \(N \le 2 ^ {10}\)，很容易想到操作次数和 \(\log N\) 有关系。

想想怎样才能和 \(\log\) 产生关系。

考虑这样的事实：

将 \(N\) 改写为二进制后，\(N\) 的位数是 \(\log N\) 级别的。

于是我们想到：

用二进制给计算机编号，最后把回答的结果整合回十进制，看看少了哪些数，就知道哪些计算机出了故障。

以第一组样例为例，我们将下面的矩阵一行一行地发送给评测机：

0 0 0 0 1
0 0 1 1 0
0 1 0 1 0

这个矩阵是什么意思呢？其实如果你竖着看，就会发现，第 \(i\) 行其实是 \(i - 1\) 的二进制表达形式。

也就是说，第 \(1\) 列就是二进制下的 \(0\)，第 \(2\) 列就是二进制下的 \(1\)，以此类推。

由于 \(0\) 和 \(3\) 出了故障，所以评测机返还给我们的是这样的：

0 0 1
0 1 0
1 0 0

整合一下，第一列是 \(1\)，第二列是 \(2\)，第三列是 \(4\)。缺少了 \(0\) 和 \(3\)，所以答案就是 0 3。

代码应该很好写，就不给了。

或者直接看后面也行。

---

考虑如何做 \(F = 5\)。

容易观察到 \(B\) 的值实际上很小，这也就意味着我们在传输信息的过程中会浪费很多列的信息。

怎么样才能防止浪费呢？

考虑下面的算法：当 \(N\) 比较大的时候，我们将每若干列分成一块。我们取 \(32\) 列分一块，这样我们每一块只存 \(0\) 到 \(31\) 的二进制表示，最后再逐块整合统计答案。

为什么这样能减少浪费，且不会产生难以辨别的漏洞呢？因为 \(B\) 最大只有 \(15\)，而块长是 \(32\)，所以即使所有的 \(B\) 在同一块内，也不会让其中一块内的计算机全部故障。

这就意味着，只要在整合后我们发现某一列的结果比后一列大，那就可以说明这两列肯定在不同的块内，我们也就可以统计答案了。

具体的，如果我们发现编号 \(i\) 有缺失，那么这台计算机就是第 \((i + 32 \times \texttt{前面出现的完整的块数})\) 台。

std

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
string s[5];
void solve() {
	int n, b, f;
	cin >> n >> b >> f;
	for (int j = 0; j < 5; j++) {
		for (int i = 0; i < n; i++) {
			cout << ((i & (1ll << j)) >> j);
		}
		cout << endl;
		cout.flush();
		cin >> s[j];
	}
	vector<int>ans(n - b + 2);
	for (int i = 0; i < n - b; i++) {
		for (int j = 0; j < 5; j++) {
			ans[i + 1] += (((int)s[j][i] - '0') << j);
		}
	}
	int las = -1;
	int cnt = -1;
	for (int i = 1; i <= n - b; i++) {
		cnt++;
		while (ans[i] != (las + 1) % 32) {
			cout << cnt << ' ';
			cnt++;
			las++;
			las %= 32;
		}
		las++;
	}
	cnt++;
	while (n % 32 != (las + 1) % 32) {
		cout << cnt << ' ';
		cnt++;
		las++;
		las %= 32;
	}
	las++;
	cout << endl;
	cout.flush();
	int x;
	cin >> x;
}
signed main() {
	int t = 1;
	cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}

D

P6008 [USACO20JAN] Cave Paintings P - 洛谷

奇怪的联通性 DP......

一个原始的想法是从下向上 DP。

但是方格之间有支配关系。考虑以下一个例子：

#####
#...#
#.#.#
#...#
#####

答案为 \(4\)，显然观察得到上层的方格一定支配下层方格，一共 \(3\) 层。

但是我们从此得知，两个方格的是否关联要基于 \(2\) 个因素：

1. 在一个联通块中；

2. 支配者层数相同或高于被支配的方格。

所以我们考虑从下向上维护并查集。

状态的转移在这里却是比较平凡的。

对于一个方格 \((x,y)\) 代表的在 \(x\) 层及以下的连通块中，若干可以联通且层数多 \(1\) 的联通块代表元素的集合为 \(S\)。

注意，\(S\) 中元素在 \(x\) 层上是联通的，但是在 \(x+1\) 层上是不联通的。

有：

\[f_{x,y} = 1+\prod_{(i,j)\in S}f_{i,j} \]

因为如果 \((x,y)\) 充水，就只有一种情况，否则 \(S\) 中块互不干扰。

所以有了 \(\mathcal O(nm)\) 次并查集 find 操作复杂度的解法。

具体实现中:

从下到上枚举每一行 \(x\)。

首先存下 \(x+1\) 的所有点在并查集中的父亲。（代表下文「合并前的并查集」。）

然后对于 \(x\) 行的空点，合并与其连通的所有点。（即「合并后的并查集」。）

再枚举 \(x+1\) 行所有空点，如果它在合并后的并查集中的祖先在 \(x\) 行，则说明它对目前答案有贡献，用它在合并前的并查集中的祖先更新合并后的并查集的祖先。

注意这里每个合并前的祖先只能贡献一次。

然后对 \(x\) 行所有点 \(f\) 值 \(+1\)。

这里有并查集合并前与合并后之分，是难理解的地方。

最后答案是所有连通块的答案之积。

std

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int  N = 1000005;
int f[N];
int ran[N];
int ans[N];
void init(int n) {
	for (int i = 0; i <= n; i++) {
		f[i] = i;
		ran[i] = 1;
		ans[i] = 1;
	}
}

int find(int x) {
	if (f[x] == x) return x;
	return f[x] = find(f[x]);
}

bool isSame(int x, int y) {
	return find(x) == find(y);
}

bool join(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y)
		return false;
	f[y] = x;
	return true;
}
string mp[1009];
int x[1009][1009];
int vis[N];
const int mod = 1e9 + 7;
signed main() {
	int n, m;
	cin >> n >> m;
	init(n * m);
	for (int i = 1; i <= n; i++) {
		cin >> mp[i];
	}
	int cnt = 0;
	for (int i = n - 1; i >= 1; i--) {
		vector<int>z;
		for (int j = 1; j < m - 1; j++) {
			if (mp[i][j] == '.') {
				if (mp[i][j - 1] == '#') {
					for (int k : z) {
						if (!isSame(cnt, k)) {
							ans[find(cnt)] *= ans[find(k)];
							ans[find(cnt)] %= mod;
							join(cnt, k);
						}
					}
					z.clear();
					cnt++;
				}
				if (mp[i + 1][j] == '.') {
					z.push_back(x[i + 1][j]);
				}
				x[i][j] = cnt;
			}
		}
		for (int k : z) {
			if (!isSame(cnt, k)) {
				ans[find(cnt)] *= ans[find(k)];
				ans[find(cnt)] %= mod;
				join(cnt, k);
			}
		}
		for (int j = 1; j < m - 1; j++) {
			if (mp[i][j] == '.') {
				int f = find(x[i][j]);
				if (vis[f]) {
					continue;
				}
				vis[f] = 1;
				ans[f]++;
			}
		}
	}
	set<int>z;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j < m - 1; j++) {
			if (mp[i][j] == '.') {
				z.insert(find(x[i][j]));
			}
		}
	}
	int anss = 1;
	map<int, int>zz;
	for (int i : z) {
		int fff = find(i);
		if (zz[fff])
			continue;
		zz[fff] = 1;
		anss *= ans[fff];
		anss %= mod;
	}
	cout << anss << endl;
	return 0;
}

E

P4145 上帝造题的七分钟 2 / 花神游历各国 - 洛谷

---

题目大意：一个序列，支持区间开方与求和操作。

算法：线段树实现开方修改与区间求和

分析：

显然，这道题的求和操作可以用线段树来维护。

但是如何来实现区间开方呢。

大家有没有这样的经历：玩计算器的时候，把一个数疯狂的按开方，最后总会变成 \(1\)，之后在怎样开方也是 \(1\) (\(\sqrt1=1\))。

同样的，\(\sqrt0=0\)。

所以，只要一段区间里的所有数全都 \(\leq 1\) 了，便可以不去修改它。

实现：

• 线段树维护区间和 \(sum\) 与最大值 \(Max\)。
• 在修改过程中，只去修改 \(Max > 1\) 的区间。
• 到了叶子节点对 \(sum\) 和 \(Max\) 进行开方就行了。

复杂度：

• 每个数 \(\leq 10 ^ {12}\),所以至多开方 \(6\) 次便可以得到 \(1\)。
• 每次操作是 \(\log n\) 的，总复杂度 \(O(n \log n)\)。

注意事项：

• 请使用long long
• 可能 \(l > r\) (把我坑了)

std

古早 std 码风很怪

点击查看代码

#define  _CRT_SECURE_NO_WARNINGS
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<set>
#include<vector>
#include<map>
#include<cmath>
#include<string>
#include<queue>
#include<stack>
#include<string.h>
#include<list>
using namespace std;
long long int a[100009];
struct tree {
	long long int l, r;
	long long pre, maxx;
};
tree t[100009 << 2];
void build(long long int p, long long int l, long long int r) {
	t[p].l = l; t[p].r = r;
	if (l == r) {
		t[p].pre = a[l];
		t[p].maxx = a[l];
		return;
	}
	long long int mid = (l + r) >> 1;
	build(p * 2, l, mid);
	build(p * 2 + 1, mid + 1, r);
	t[p].pre = t[p * 2].pre + t[p * 2 + 1].pre;
	t[p].maxx = max(t[p * 2].maxx, t[p * 2 + 1].maxx);
}
void change(long long int p, long long int x, long long int y) {
	if (x <= t[p].l && y >= t[p].r && t[p].l == t[p].r) {
		t[p].pre = sqrt(t[p].pre);
		t[p].maxx = t[p].pre;
		return;
	}
	long long int mid = (t[p].l + t[p].r) >> 1;
	if (x <= mid && t[p * 2].maxx > 1)
		change(p * 2, x, y);
	if (y > mid && t[p * 2 + 1].maxx > 1)
		change(p * 2 + 1, x, y);
	t[p].pre = t[p * 2].pre + t[p * 2 + 1].pre;
	t[p].maxx = max(t[p * 2].maxx, t[p * 2 + 1].maxx);
}
long long int ask(long long int p, long long int x, long long int y) {
	if (x <= t[p].l && y >= t[p].r)
		return t[p].pre;
	long long int mid = (t[p].l + t[p].r) >> 1;
	long long ans = 0;
	if (x <= mid)
		ans += ask(p * 2, x, y);
	if (y > mid)
		ans += ask(p * 2 + 1, x, y);
	return ans;
}
int main() {
	long long int n, m;
	scanf("%lld", &n);
	for (long long int i = 1; i <= n; i++) {
		scanf("%lld", &a[i]);
	}
	build(1, 1, n);
	scanf("%lld", &m);
	for (long long int i = 1; i <= m; i++) {
		long long int q, x, y;
		scanf("%lld", &q);
		if (q == 0) {
			scanf("%lld%lld", &x, &y);
			if (x > y)
				swap(x, y);
			change(1, x, y);
		}
		else {
			scanf("%lld%lld", &x, &y);
			if (x > y)
				swap(x, y);
			printf("%lld\n", ask(1, x, y));
		}
	}
	return 0;
}

F

P10930 异象石 - 洛谷

本题的思考分为两个部分，第一个部分是如何求出连通边集最小大小，第二部分是如何在线维护这个大小。

求连通点边集最小大小

我们可以将问题转化成以一个异象石点所在点为起点，如何以最少的步数将所有点遍历最后回到起点。

如图，最少步数的走法是从 \(1\) 开始，然后绕着所有异象石的外围走一圈，也就是将异象石按 dfs 序的顺序走一遍，这样所用的步数其实就是我们要求的这个边集大小的两倍，我们只要统计这个步数最后 \(\div 2\) 即可。

动态统计的方法

我们可以用 set 等数据结构来维护。

• 当异象石的点集为空时，显然加入点时不会影响答案。
• 当异象石的点集不为空时，加入一个点就是将答案加上它分别与左右两个异象石的距离并减去左右两个异象石互相的距离，删除异象石则反之。特别的，我们将点集看作一个环，所以如果插入或删除的点位于排序后的最左边或最右边，那么它的左边点或右边点为最右点或最左点。

两个点的距离我们可以用 LCA（最近公共祖先）维护。

具体实现

先建树，再预处理树上每个点的 dfs 序，然后在线处理询问即可。

std

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
vector<pair<int, int>>tree[500009];
int siz[500009];
int fa[500009];
int son[500009];
int top[500009];
int dep[500009];
int d[500009];
int cnt = 0;
int dfn[500009];
void dfs1(int u, int f, int w) {
	dfn[u] = ++cnt;
	dep[u] = dep[f] + w;
	d[u] = d[f] + 1;
	fa[u] = f;
	siz[u] = 1;
	int maxx = 0;
	for (auto i : tree[u]) {
		if (i.first == f)
			continue;
		dfs1(i.first, u, i.second);
		siz[u] += siz[i.first];
		if (siz[i.first] > maxx) {
			maxx = siz[i.first];
			son[u] = i.first;
		}
	}
}
void dfs2(int u, int f) {
	top[son[u]] = top[u];
	for (auto i : tree[u]) {
		if (i.first == f)
			continue;
		dfs2(i.first, u);
	}
}
int LCA(int a, int b) {
	while (top[a] != top[b]) {
		if (d[top[a]] < d[top[b]])
			swap(a, b);
		a = fa[top[a]];
	}
	if (d[a] > d[b])
		return b;
	else
		return a;
}
void init(int n, int root) {
	dfs1(root, 0, 0);
	for (int i = 1; i <= n; i++) {
		top[i] = i;
	}
	fa[root] = root;
	dfs2(root, 0);
}
int getdis(int u, int v, int l) {
	return dep[u] + dep[v] - 2 * dep[l];
}
signed main() {
	int n;
	cin >> n;
	for (int i = 1; i < n; i++) {
		int x, y, z;
		cin >> x >> y >> z;
		tree[x].push_back({ y,z });
		tree[y].push_back({ x,z });
	}
	init(n, 1);
	int q;
	cin >> q;
	set<pair<int, int>>s;
	int ans = 0;
	while (q--) {
		char op;
		cin >> op;
		if (op == '+') {
			int x;
			cin >> x;
			if (s.size() == 1llu) {
				int t = LCA((*s.begin()).second, x);
				ans = getdis(x, (*s.begin()).second, t) * 2;
			}
			else if (s.size() > 1) {
				int l, r;
				if (dfn[x] < (*s.begin()).first || (*s.rbegin()).first < dfn[x]) {
					l = (*s.begin()).second, r = (*s.rbegin()).second;
				}
				else {
					auto it = s.lower_bound({ dfn[x],x });
					r = (*it).second;
					it--;
					l = (*it).second;
				}
				int t;
				t = LCA(l, x);
				ans += getdis(x, l, t);
				t = LCA(r, x);
				ans += getdis(x, r, t);
				t = LCA(l, r);
				ans -= getdis(l, r, t);
			}
			s.insert({ dfn[x],x });
		}
		else if (op == '-') {
			int x;
			cin >> x;
			auto it = s.lower_bound({ dfn[x], x });
			auto ed = s.end();
			if (s.size() == 1llu || s.size() == 2llu) {
				ans = 0;
			}
			else {
				ed--;
				int l, r;
				if (it == s.begin()) {
					ed = s.begin();
					r = (*s.rbegin()).second;
					ed++;
					l = (*ed).second;
				}
				else if (it == ed) {
					l = (*s.begin()).second;
					ed--;
					r = (*ed).second;
				}
				else {
					it++;
					r = (*it).second;
					it--, it--;
					l = (*it).second;
					it++;
				}
				int t;
				t = LCA(l, x);
				ans -= getdis(x, l, t);
				t = LCA(r, x);
				ans -= getdis(x, r, t);
				t = LCA(l, r);
				ans += getdis(l, r, t);
			}
			s.erase(it);
		}
		else {
			cout << ans / 2 << endl;
		}
	}
	return 0;
}

G

P4747 [CERC2017] Intrinsic Interval - 洛谷

第一场最后一题的后续题目。

析合树解法，缺点是代码确实有点长，优点是基于析合树看这个问题就变得非常显然了。

析合树是一种方便处理连续段\(^1\)相关问题的数据结构，我们简单介绍一下流程：

对于给定的序列，连续段的数量是 \(O(n^2)\) 的，显然不可能用 \(O(n^2)\) 的连续段来构造析合树，于是引入本原连续段\(^2\)，容易发现，如果两个连续段之间没有包含关系，那么他们一定各自独立，且任意一个连续段都可以被一个或多个本原连续段组成，由于原序列是 \(1 \sim n\) 的一个排列，故原序列也是一个本原连续段，而且是所有本原连续段中最大的那个。

于是以原序列为根节点，其他本原连续段为其他结点，包含关系作为边，建得一棵析合树，注意现在的结点不再是一个数而是一个区间，单个数 \(x\) 可以看成形如 \([x,x]\) 的区间。

• 合点：将一个结点的儿子结点按值域离散化后组成的排列有序，则这个结点为合点。

• 析点：不满足合点性质的点。

使用增量法建树，时间复杂度 \(O(n \log n)\)。

考虑用一个栈维护前 \(i-1\) 个结点（注意栈中的结点数目不一定为 \(i-1\)），对于第 \(i\) 个结点：

1. 尝试与栈顶结点连边，如果可以连边则结束，将栈顶结点当作第 \(i\) 个结点考量。

2. 尝试与栈顶结点合并，如果可以合并则结束，将合并后的结点当作第 \(i\) 个结点考量。

连边很简单，考虑合并操作：

首先考虑另一个问题：我如何知道一个子段是连续段？

通过连续段的定义，我们很容易推出判定条件：区间极差与区间长度的差为 \(-1\)。

不难想到使用 ST表 维护这个区间极差，时间复杂度 \(O(n\log n)-O(1)\)。

显然这样维护静态区间是很好处理的，但是增量的过程中，区间是在不断变化的，这样单纯寻找这样一个条件就不现实了。

对它进行一个移项，令 \(q_k\) 为区间 \([k,i]\) 中极差与区间长度的差再减一，这样我们的条件就变成了 \(q_k=0\)。

令 \(pos\) 为满足这个条件且包含当前结点所表示区间的左端点最大值，发现这个形式很像单调栈，于是增量的过程使用单调栈来维护。要获取这个 \(pos\)，只需要知道 \(q\) 中满足 \(q_i=0\) 的 \(i\) 的最大值即可。查询 \(q_i=0\) 可以变为查找 \(q_i\) 的最小值，\(pos\) 即为这个最小值所在的位置。

当下次增量操作开始，所有存储的区间长度均会增加一，所以我们对 \(q\) 全体减一来维护，既要查询最小值，又要区间减，于是考虑使用线段树来维护 \(q\)。

最后具体到这个题目来说，我们找到给定 \(l_i,r_i\) 所对应结点的 \(\rm LCA\)。如果此结点为合点，答案为 \(l_i,r_i\) 对应形成的儿子区间；如果此节点为析点，答案即为它所对应的区间。

连续段\(^1\)：值域连续的区间，即 \([l,r]\) 满足 \(\nexists x,y \in [l,r],k \notin [l,r],a_x<a_k<a_y\)。

本原连续段\(^2\)：对于一个连续段，如果在原序列中所有的连续段中，不存在其他的连续段和它相交且并不属于它，那么认为这个连续段是本原连续段。

std

std 用了析合树板子，有详细的注释。

点击查看代码

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int MAXN = 1e5 + 5;
int n, a[MAXN];
struct NODE {
	int l, r; bool type; // 每一个结点的值域区间与类型（析/合）
	NODE(int l = 0, int r = 0, bool type = 0) : l(l), r(r), type(type) {}
}t[MAXN << 1]; // 注意点数是 2n-1，因此要开两倍空间
// 每一个结点的儿子序列，其实也就是出边
vector < int > d[MAXN << 1];
// 这里对于每一个结点要多维护一个 M 表示其最右侧的一个儿子的左端点，方便判断当前点是否可以成为栈顶的新儿子，详细的可以看 build() 函数
int tot = 0, M[MAXN << 1];
struct Segtree {
	int t[MAXN << 2], tag[MAXN << 2];
	void pushup(int rt) {
		t[rt] = min(t[rt << 1], t[rt << 1 | 1]);
	}
	void update(int rt, int z) {
		t[rt] += z;
		tag[rt] += z;
	}
	void pushdown(int rt) {
		if (tag[rt]) {
			update(rt << 1, tag[rt]);
			update(rt << 1 | 1, tag[rt]);
			tag[rt] = 0;
		}
	}
#define LSON rt << 1, l, mid
#define RSON rt << 1 | 1, mid + 1, r
	void build(int rt, int l, int r) {
		tag[rt] = 0;
		if (l == r) return t[rt] = l, void();
		int mid = (l + r) >> 1;
		build(LSON); build(RSON);
		pushup(rt);
	}
	int query(int rt, int l, int r) { // 找出最左的一个 0
		if (l == r) return l;
		int mid = (l + r) >> 1; pushdown(rt);
		return t[rt << 1] ? query(RSON) : query(LSON);
	}
	int ask(int rt, int l, int r, int x) { // 单点查询，若是 0 则说明可以形成连续段
		if (l == r) return t[rt];
		int mid = (l + r) >> 1; pushdown(rt);
		return x <= mid ? ask(LSON, x) : ask(RSON, x);
	}
	void modify(int rt, int l, int r, int x, int y, int z) { // 区间修改
		if (x <= l && r <= y) return update(rt, z);
		int mid = (l + r) >> 1; pushdown(rt);
		if (x <= mid) modify(LSON, x, y, z);
		if (y > mid) modify(RSON, x, y, z);
		pushup(rt);
	}
}sgt;
int stk1[MAXN], tp1, stk2[MAXN], tp2, s[MAXN], tp;
int id[MAXN], root;
// 树剖求 LCA
int dep[MAXN << 1], tt[MAXN << 1], fa[MAXN << 1], sz[MAXN << 1], son[MAXN << 1];
void dfs(int x) {
	sz[x] = 1; for (auto v : d[x]) {
		fa[v] = x; dep[v] = dep[x] + 1;
		dfs(v); sz[x] += sz[v];
		if (sz[v] > sz[son[x]]) son[x] = v;
	}
}
void dfs2(int x, int lt) {
	tt[x] = lt; if (son[x]) dfs2(son[x], lt);
	for (auto v : d[x]) if (v != son[x]) dfs2(v, v);
}
int LCA(int x, int y) { // 树剖求 LCA
	while (tt[x] ^ tt[y]) {
		if (dep[tt[x]] < dep[tt[y]]) swap(x, y);
		x = fa[tt[x]];
	}
	return dep[x] > dep[y] ? y : x;
}
void build() {
	sgt.build(1, 1, n); // 建树，初值为 l
	for (int i = 1; i <= n; i++) {
		sgt.update(1, -1); // 右端点移动时全局减
		// 单调栈维护 max/min 常数似乎小一些，注意弹栈时要撤销贡献
		while (tp1 && a[i] <= a[stk1[tp1]]) {
			sgt.modify(1, 1, n, stk1[tp1 - 1] + 1, stk1[tp1], a[stk1[tp1]]);
			--tp1;
		}
		while (tp2 && a[i] >= a[stk2[tp2]]) {
			sgt.modify(1, 1, n, stk2[tp2 - 1] + 1, stk2[tp2], -a[stk2[tp2]]);
			--tp2;
		}
		sgt.modify(1, 1, n, stk1[tp1] + 1, i, -a[i]);
		stk1[++tp1] = i;
		sgt.modify(1, 1, n, stk2[tp2] + 1, i, a[i]);
		stk2[++tp2] = i;
		// 建立一个新的待插入结点
		t[id[i] = ++tot] = NODE(i, i, 0);
		const int lim = sgt.query(1, 1, n);
		int u = tot;
		while (tp && t[s[tp]].l >= lim) { // 注意这里要反复进行
			if (t[s[tp]].type && !sgt.ask(1, 1, n, M[s[tp]])) { // 第一类分讨，看是否能成为儿子
				t[s[tp]].r = i;
				M[s[tp]] = t[u].l;
				d[s[tp]].push_back(u);
				u = s[tp--];
			}
			else if (!sgt.ask(1, 1, n, t[s[tp]].l)) { // 第二类分讨，看是否能合并
				t[++tot] = NODE(t[s[tp]].l, i, 1);
				M[tot] = t[u].l;
				d[tot].push_back(s[tp--]);
				d[tot].push_back(u);
				u = tot;
			}
			else { // 第三类分讨，尽可能少的结点合并建立析点
				d[++tot].push_back(u);
				do {
					d[tot].push_back(s[tp--]);
				} while (tp && sgt.ask(1, 1, n, t[s[tp]].l));
				t[tot] = NODE(t[s[tp]].l, i, 0);
				d[tot].push_back(s[tp--]);
				u = tot;
			}
		}
		s[++tp] = u; // 最后入栈
	}
	dep[root = s[1]] = 1;
	dfs(root);
	dfs2(root, root); // 建析合树
}
bool cmp(int x, int y) {
	return t[x].l < t[y].l;
}
signed main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	build();
	int q;
	cin >> q;
	while (q--) {
		int l, r;
		cin >> l >> r;
		l = id[l]; r = id[r];
		int lca = LCA(l, r);
		if (t[lca].type) {
			auto L = upper_bound(d[lca].begin(), d[lca].end(), l, cmp);
			auto R = upper_bound(d[lca].begin(), d[lca].end(), r, cmp);
			int ll = *(--L);
			int rr = *(--R);
			cout << t[ll].l << ' ' << t[rr].r << endl;
		}
		else {
			cout << t[lca].l << ' ' << t[lca].r << endl;
		}
	}
	return 0;
}