基础图论学习笔记

有向无环图（DAG）和拓扑排序

拓扑排序是解决 DAG 上问题的利器。

【例题 1】P2505 [HAOI2012] 道路

对于每个点为原点分别计算，记 \(\mathrm{dis}_i\) 表示到 \(i\) 的最短路。

对于一条边 \((u, v,w)\) ，若 \(\mathrm{dis}_u + w > \mathrm{dis}_v\)，则这条边是不可能成为答案的，所以只有 \(\mathrm{dis}_u + w = \mathrm{dis}_v\) 的边才可能作为答案，扣出所有这样的边，得到图称为最短路 DAG。

在最短路 DAG 上的一条边 \((u, v)\)，可能经过的次数就是从起点开始到 \(u\) 的方案数乘上 \(v\) 到终点的方案数，可以通过正反两边拓扑排序结局。

【例题 2】P3243 [HNOI2015] 菜肴制作

首先，题目要求的不是字典序最小，例如 \((2, 4, 1, 3)\) 劣于 \((3, 1, 2, 4)\)，但是可以发现，大的数字在后面是一定不劣的，于是自然得到答案就是反字典序最大的拓扑序。

要得到字典序最大，只需要把队列换成优先队列即可。

【例题 3】[AGC010E] Rearranging

首先注意到若 \(x, y\) 不互质，则两者的相对位置是不能改变的。方便起见，下文对序列进行了排序。

我们把相对位置不能改变的数对两两连边，得到一个无向图。因为高桥君希望字典序尽可能小，在这些不能交换的关系中，他一定是从小到大给出的。于是我们可以跑一个 DFS 树出来，每次向最小的点走，因为字典序是一个经典的贪心，所以这样显然是对的。

最后轮到青木君来操作，那么他会选择最大的拓扑序，使用优先队列即可。

【例题 4】P7831 [CCO2021] Travelling Merchant

好题。

设 \(f_u\) 表示要从 \(u\) 开始能无限走所需要的最小的初始权值，对于一条边 \((u,v,r,p)\) 容易得到 \(f_u = \min(f_u, \max(r, f_v - p))\)，但是环上的 DP 显然做不了。

首先发现：出度为 \(0\) 的点显然无解，那么可以把这些点删去。

然后发现：在一个图中，如果以 \(\max(r)\) 为初始权值，一定能走下去。

那么我们从大到小考虑每一条边 \((u, v, r, p)\)，首先删去出度为 \(0\) 的点，用其更新其他点（这是因为此时显然这个点的答案已经确定了），实际上就是做一个拓扑排序。

然后判断一下当前这条边有没有被删除，如果没有，那么考虑用 \(v\) 更新 \(u\) 的答案，然后删去这条边。因为我们是按照 \(r\) 从大到小考虑的，此时更新的答案可能偏大，但是不会影响后面的决策。

【例题 5】P9534 [YsOI2023] 广度优先遍历

拓扑排序还可以用来解决偏序关系的构造问题。

对于这个题，我们考虑一条边 \((u, v)\)，若其连接了两个同层的点，那么这条边显然是没用的，顺序可以随意钦定，否则这一定连接了两个相邻的层，否则无解，因为 BFS 树实际上也是一个最短路树。

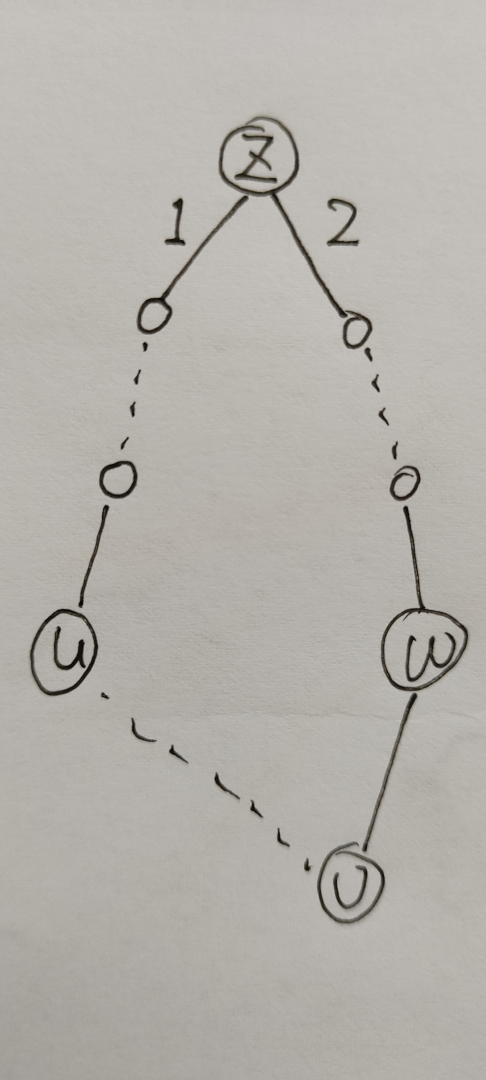
借用官方题解的图，发现连 \((w,v)\) 而不是 \((u,v)\) 的充要条件为边 \(1\) 在边 \(2\) 后面出现，那么就有了一个偏序关系，找到一个拓扑序即可。

最小生成树

普通的 Prim 和 Kruskal 就不说了。

Boruvka

【例题 0】CF888G Xor-MST

Boruvka 是一种最小生成树算法，用于求解稠密图的 MST。

基本流程：首先初始化每个连通块为自身，每次对于 \(u \in S\) 找到满足题意的最小的边连到 \(v \notin S\) 并把两个连通块合并。直到只剩下一个连通块，也就是整个图联通。

因为每次都至少把连通块数量除以二，所以只需要做 \(\log_2 n\) 次即可。

我们用并查集维护集合关系，我们在每次循环开头判断当前连通块个数。

int cnt = 0;
F(i, 1, n) {
    if (f[i] == i) {
        bl[i] = cnt + 1; 
        cnt++;
        to[cnt] = val[cnt] = -1;
    }
}
if (cnt == 1) break;

一般的，我们把 to[x] 和 val[x] 记为从 x 这个连通块出发能到达的满足条件的最优点和边权。

我们考虑一下本题，怎么找“最优边”？异或最小，显然想到使用 01-Trie 维护，但是我们需要写的是支持删除的 01-Trie 所以需要额外记录 \(\text{size}\)。

复杂度是 Boruvka 的本身 \(\mathcal{O}(n\log n)\) 乘上你需要额外支持快速查询最小边的数据结构的复杂度，在本题中为 \(\mathcal{O}(\log V)\)，\(V\) 为值域。

总复杂度 \(\mathcal{O}(n\log n \log V)\) 常数也较大，注意卡常。

【例题 1】P4197 Peaks

这个题引入了 Kruskal 重构树的概念。

在跑 Kruskal 的过程中我们会从小到大加入若干条边。现在我们仍然按照这个顺序。

首先新建 \(n\) 个集合，每个集合恰有一个节点，点权为 \(0\)。

每一次加边会合并两个集合，我们可以新建一个点，点权为加入边的边权，同时将两个集合的根节点分别设为新建点的左儿子和右儿子。然后我们将两个集合和新建点合并成一个集合。将新建点设为根。

不难发现，在进行 \(n - 1\) 轮之后我们得到了一棵恰有 \(n\) 个叶子的二叉树，同时每个非叶子节点恰好有两个儿子。这棵树就叫 Kruskal 重构树。

来自 OI-wiki

这个重构树有很多优美的性质，以最小生成树为例，\((x,y)\) 的 LCA 的权值就是两点路径上的最大边权，那么我们可以倍增跳到困难值小于等于 \(x\) 的最高点，这个点的子树都是可达的，问题变成求子树 \(k\) 小值，主席树即可。

【例题 2】P9488 ZHY 的生成树

这个题有点启发，如果 \(\mathcal{O}(n^2)\) 的建边行不通，可以考虑缩小边权，因为这个题数据范围很大，不会去考虑 Boruvka，发现每个点都只和自己的倍数去连边就行了，这样是 \(\mathcal{O}(n \ln n)\) 的，还是过不去，发现有许多数被反复枚举了，那么我们改成枚举质数倍即可，最终复杂度 \(O(n \ln \ln n)\)。

【例题 3】CF1981E Turtle and Intersected Segments

同样是完全图，要么考虑 Boruvka，要么考虑减少边的数量。这题 Boruvka 是 \(\mathcal{O}(n \log^2 n)\) 的，比较不牛。

观察两两相交的线段 \((l_1,r_1,a_1)\)，\((l_2,r_2,a_2)\)，\((l_3,r_3,a_3)\)，不妨认为 \(a_1 < a_2 < a_3\)，那么发现 \(|a_1 - a_3|\) 这个边一定是没用的，我们把边在 \(l\) 处加入，在 \(r\) 处删除，加入的时候查询一下 \(a\) 的前驱和后继，向它们连边即可，这样边数就缩减到了 \(\mathcal{O}(n)\)。

最短路

单源最短路一般使用 Dijkstra，全源最短路一般使用 Floyd 和 Johnson 算法。

【例题 1】P4768 [NOI2018] 归程

可以用上文提到的 Kruskal 重构树解决第一部，我们发现此时要查询的是子树内的点到 \(1\) 号点最短路的最小值，那么直接维护一下就好了。

【例题 2】P4568 [JLOI2011] 飞行路线

经典的分层图。观察到 \(k\le 10\)，我们可以记录 \(\mathrm{dis}_{i,j}\) 表示到 \(i\) 用了 \(j\) 次免费机会的最短路，这其实就是在 DP 的过程中加入了一维状态。

【例题 3】CF295B Greg and Graph

思考 Floyd 的最外层循环到底是在干什么，这其实是一个不断加入点的过程，那么我们倒序做一遍就好了。

【例题 4】gym100917F Find the Length

对于一个点 \(u\) 的答案，我们直接枚举 \(i,j\)，答案就是 \(\min(w_{u,i} + w_{j,v} + \mathrm{dis}_{i,j})\)，此时的最短路是不能经过 \(u\) 的，也就是我们要知道删去一个点的最短路情况，可以分治解决这个问题。

具体的，我们加入一个点，先加入和其相连的边，然后用这个点，像 Floyd 一样更新和其他点之间的最短路。

【例题 5】CF1051F The Shortest Statement

发现这个图就是一个树随机加上 \(m - n \le 20\) 条边，最终的最短路要么不经过这些边，直接树上求一下距离即可，否则我们把这些点标记出来，分别求一个单源最短路，查询的时候枚举一个点 \(\mathrm{dis}_{i,x} + \mathrm{dis}_{i,y}\) 就是答案，这种枚举中间点或边的方法也是很常见的。

【例题 6】P5905 全源最短路（Johnson）

首先我们用 Bellman-Ford 或 SPFA 跑出从一个超级源点到所有点的最短路，记为 \(h_i\)，对于原图中的一条边 \((u,v,w)\)，我们把边权改为 \(h_u + w - h_v\)，这样可以保证边权非负，否则 \(h_v\) 就不是最短路了，那么可以启动一个 Dijkstra，直接做到 \(\mathcal{O}(n(n + m)\log m)\)。

正确性考虑途中的一条路径 \(s \leadsto t\)，那么现在的边权是 \(\sum w + h_s - h_t\)，因为 \(h_s - h_t\) 是不变的，那么这条路径最小当且仅当 \(\sum w\) 最小，也就是这和原图中的最短路一一对应。

【例题 7】CF843D Dynamic Shortest Path

暴力是 \(O(q(n + m)\log m)\) 的，每次跑 Dijkstra，但是实际上我们只想要知道最短路的增量即可，借用 Johnson 算法的思想，新的边权设为 \(\mathrm{dis}_u + w - \mathrm{dis}_v\)，在这个图上我们得到的最短路就是增量大小，而一次操作导致的增量变化是至多是 \(n- 1\)，于是我们可以开桶来记录边权，每次相当于在队列中操作，这样就可以做到 \(O(n + m)\) 求最短路。

0-1 BFS 扩展到 a-b BFS

开两个队列，经过 \(a\) 边的点放一个，经过 \(b\) 边的点放另一个，每次两个队列头部取出最小的转移即可。

差分约束

这个可以用来判断若干个变量之间的不等式关系是否合法并给出一组解。

观察一个不等式 \(x_i + c \ge x_j\)，把 \(x_i\) 想象成是图上某个点到 \(i\) 的最短路，根据最短路的三角形不等式，我们连边 \((i,j,c)\) 即可。

其他不等式都可以转化成这个形式，有没有解判断负环即可。

【例题 1】P4926 倍杀测量者

对于 \(\dfrac{x_i}{x_j} \le c\) 的约束条件，我们可以两边取一个 \(\log\)，转化成了 \(\log x_i - \log x_j \le \log c\)，直接按照上文的方法解决即可。

同余最短路

我不会转圈算法，成为了时代的眼泪。

可以高效的解决一些背包问题。

【例题 1】P2371 [国家集训队] 墨墨的等式

我们钦定一个物品 \(a_i\)，对于其他的物品，其在 \(\bmod a_i\) 意义下若能凑出 \(x\)，则最后 \(x + ka_i\) 就是能被表示出来的，这个可以模拟连边，跑最短路即可。

连通性问题（Tarjan）

强连通分量

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。

这里要介绍的是如何来求强连通分量。

首先要了解 DFS 树，如下图所示。

DFS 生成树

红色的边连向自己的祖先，称为返租边，绿色的边连向自己的字数中的点，称为前向边，蓝色的边连接两个不同的子树，称为横叉边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。

记录 \(\mathrm{dfn}_i\) 表示到 \(i\) 的遍历顺序，\(\mathrm{low}_i\) 表示从 \(i\) 的子树出发，能到达的在搜索栈中的点的 \(\mathrm{dfn}\) 最小值。

int dfn[N], low[N], ins[N], s[N], scc[N];
vector<int> G[N];
void tarjan(int u) {
    low[u] = dfn[u] = ++cnt;
    s[++top] = u, ins[u] = 1;
    for(auto i : G[u]) {
        if(!dfn[i]) {
            tarjan(i);
            low[u] = min(low[u], low[i]);
        } else if (ins[i]) {
            low[u] = min(low[u], dfn[i]);
        }
    }
    if(low[u] == dfn[u]) {
        scc[u] = ++cscc;
        do {
            ins[s[top]] = 0;
            scc[s[top]] = cscc;
        } while(s[top--] != u) ;
    }
}

有向图 SCC 可以用来缩点，这样可以把图变成 DAG，在遇到可以重复经过点的问题的时候会考虑。

无向图的双连通分量

分为边双和点双。

一些性质：

一条边恰好在一个点双内，至多在一个边双内。
一个点恰好在一个边双内，可以同时位于多个点双内。
割边不在任何一个边双内。将所有割边删去后，剩下的每个连通块即为原图的所有边双。非割边恰好在一个边双内。割点一定在多个点双内（即若干点双的交点）。非割点恰好在一个点双内。
有向图缩点之后是 DAG，边双缩点之后是树，点双可以考虑建立圆方树。

【例题 1】NOIP 模拟赛 T3

小 T 在筹集自己的势力，但是他不小心误入了夜落的陷阱，他发现有一个 \(n\) 个结点，\(m\) 条边的无向简单图，所有结点编号为 \(1\) 到 \(n\)，第 \(i\) 条边为 \((a_i,b_i),(1 ≤ i ≤ m)\)。

他准备用 \(k\) 种颜色对无向图的所有边染色。由于他的染料充足，每种颜色可以染任意多条边（也可以是 \(0\) 条）。

这张图有一个神奇的特性：小 T 可以选择图中任意一个简单环（即不经过重复结点的环），然后将环上的边的颜色循环移动一位。形式化地，设 \(e_1 , e_2 , \dots , e_a\) 为沿着简单环走一圈依次经过的边，那么 \(e_2\) 的颜色变为 \(e_1\) 原来的颜色，\(e_3\) 的颜色变为 \(e_2\) 原来的颜色，......，\(e_a\) 的颜色变为 \(e_{a−1}\) 原来的颜色，且 \(e_1\) 的颜色变为 \(e_a\) 原来的颜色。
他发现只需要求出有多少种不同的染色方案，输出答案对 \(10^9 + 7\) 取模的结果。

题目是对边的操作，而一条边恰好在一个点双内，所以要考虑点双！赛时我一直考虑在边双上做这个问题，结果做不出来。

在点双上有一个很牛的结论：如果不是一个大环，点双内边可以任意交换。

但是在边双上是不行的。

对于可以任意交换的情况，答案是一个组合数，那么可以使用插板法计算。

那么只要解决只有一个大环的情况即可，可以利用循环节长度来容斥计算，设 \(f_i\) 表示循环节长度为 \(i\) 的环的方案数量，那么 \(f_i = k^i - \sum_{i | j}f_j\)，复杂度是调和级数。

【例题 2】QOJ 8686. Zoo Management

这个就是上题的点双变成边双，没有了那么好的结论，做法待补，我还不会。

圆方树

如果题目和割点有关，要查询两个点上路径信息的并，那么可以考虑一下圆方树。

【例题 1】P4320 道路相遇

从一个点到另一个点，必经的点，显然需要是割点，否则就是可以绕过的。

那么要求的是两点之间割点的数量，我们知道圆方树上两个方点之间的点就是割点，那么直接计算树上路径长度即可。

【例题 2】CF487E Tourists

比较 naive 的想法是每个方点表示相连的圆点的权值 \(\min\)，这样的话更新一个点是 \(\mathcal{O}(n)\) 的，不妨只让其存储儿子的信息，查询的时候判断一下 LCA 的父亲即可，然后可以 \(\text{multiset}\) 加上树剖维护掉。

2-SAT 问题

2-SAT，简单的说就是给出 \(n\) 个集合，每个集合有两个元素，已知若干个 \((a, b)\)，表示 \(a\) 与 \(b\) 矛盾（其中 \(a\) 与 \(b\) 属于不同的集合）。然后从每个集合选择一个元素，判断能否一共选 \(n\) 个两两不矛盾的元素。显然可能有多种选择方案，一般题中只需要求出一种即可。

常见的方法是利用 Tarjan 来缩点后计算。

如果 \(a\) 和 \(\neg a\) 在同一个 SCC 内，显然无解，否则考虑给出一种构造，我们得到 SCC 的顺序就是一个反拓扑序。

如果 \(a\) 的拓扑序比 \(\neg a\) 小，那么说明 \(a \rightarrow \neg a\)，也就是选 \(a\)，否则选 \(\neg a\)。

没啥好的例题。

欧拉图

无向图：

欧拉回路：每个点度数都是偶数。
欧拉路径：\(0\) 或 \(2\) 个点度数是奇数。

有向图：

欧拉回路：每个点入度等于出度
欧拉路径：要么是欧拉回路，要么恰好有一个点 \(\mathrm{ind}_i = \mathrm{outd}_i + 1\)，有一个点 \(\mathrm{ind}_i = \mathrm{outd}_i - 1\)。

一般遇到问题让你首尾相接的可以考虑。

二分图

可以把图分成左右两部，同一部的点之间没有连边，不同之间有连边，有很多性质。

最小点覆盖：选最少的点，满足每条边至少有一个端点被选，二分图中，最小点覆盖 \(=\) 最大匹配。
最大独立集：选最多的点，满足两两之间没有边相连。

因为在最小点覆盖中，任意一条边都被至少选了一个顶点，所以对于其点集的补集，任意一条边都被至多选了一个顶点，所以不存在边连接两个点集中的点，且该点集最大。因此二分图中，最大独立集 \(=\) 最小点覆盖。

解决二分图问题很多时候需要用到网络流或者匈牙利算法。

【例题】[ABC227H] Eat Them All

如果我们知道了每个边的经过次数，是容易构造一个欧拉回路的。

然后发现一个点一进一出恰好就是 \(1\) 的贡献，那么要 \(a\) 的贡献要求周围边的经过次数为 \(2a\)，网格图是经典的二分图，那么可以直接用最大流去得到一组解。

但是得到的图可能不联通，那么可以指数级的去枚举一个生成树，保证其联通。

图论技巧与杂项

建立虚点

【例题 1】[ARC061E] すぬけ君の地下鉄旅行

对于同一种线路之间，显然都可以以 \(1\) 的代价互相到达，直接连完全图是不牛的，我们可以搞一个虚点出来，每个点向虚点连边就能达到一样的效果。

【例题 2】CF1775D Friendly Spiders

如果两个数字 \(\gcd\) 不为 \(1\)，那么其一定有公共的质因子，对其建立虚点，那么每个点向其质因子连边可以得到等价的连通性。

posted @ 2024-07-18 06:59 紊莫阅读(61) 评论(0) 收藏举报

刷新页面返回顶部

Loading

紊莫的博客

基础图论学习笔记