FPGA 有限状态机的写法

逻辑电路可以分为两大类：“组合”逻辑电路和“时序”逻辑电路。组合逻辑电路的输出只取决于当前的输入。时序逻辑电路的输出不仅取决于当前的输入，而且取决于过去的输入序列，这个序列是任意长的。

对于组合逻辑电路，可以通过输入输出之间的真值表来描述其功能。而对于时序逻辑电路，使用真值表描述其功能是不现实的，无法确定需要取一个多长的输入组合取值序列，因此时序逻辑电路一般采用有限状态机作为电路行为的描述。

有限状态机主要由数量有限的状态和状态之间的转换规则组成。数字逻辑电路中的状态变量都是二进制数值，对应着电路中的某些逻辑信号。如交通信号灯电路中，不同信号灯的亮灭可以使用数个二进制值来表示。时序电路的状态变化大多依靠时钟信号来规定，在时钟的边沿，状态机根据规则转换当前的状态。

1. D触发器

大多数时序电路均采用D触发器来存储它们的状态变量，上升沿触发的D触发器逻辑符号和功能表如图所示。

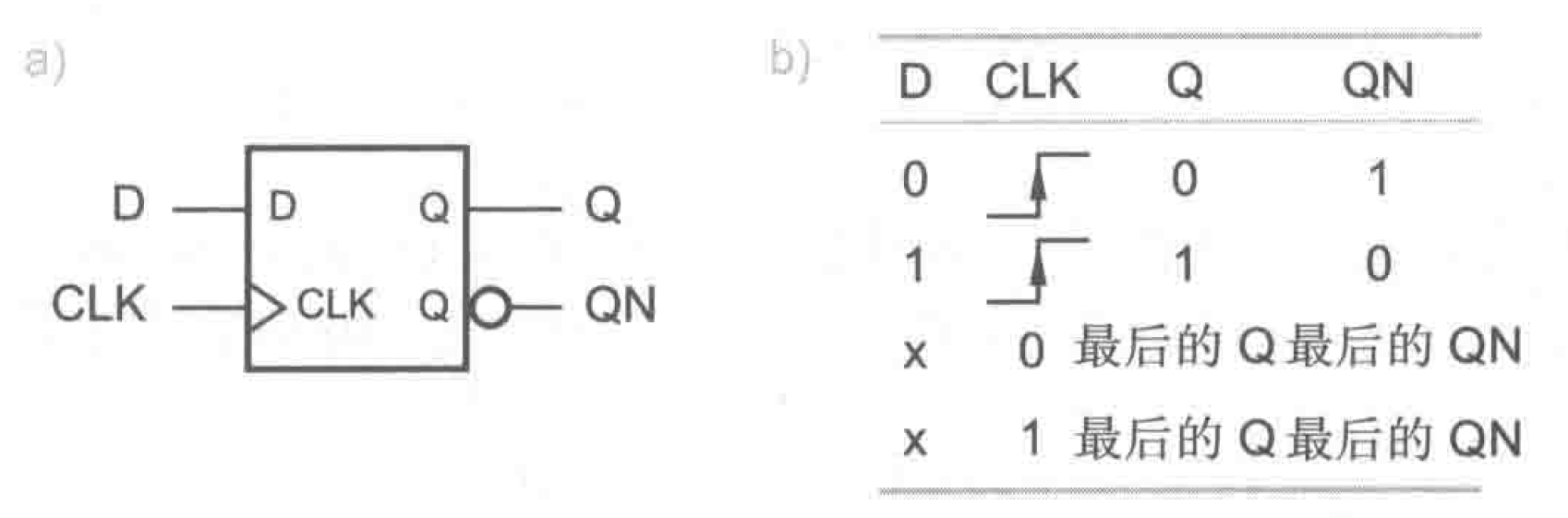
电路的输入是数据信号D和时钟信号CLK，输出为Q以及可选的QN（Q补）。当CLK从低电平转换到高电平时，电路对D进行采样，并把Q置为当前D的值（QN置为D的反）。上述CLK从低电平到高电平的变化期间，Q（以及QN）的值保持不变。下图展示了一个上升沿触发的D触发器针对所举例的输入序列的功能特性。

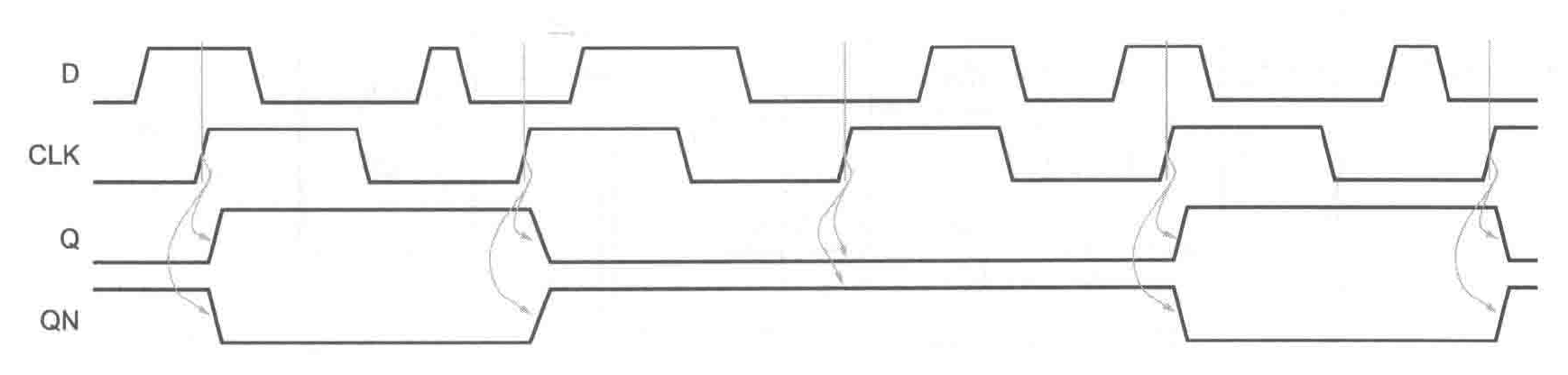
在Verilog中可以使用行为建模对正边沿触发的D触发器建模，如下所示。

module D_ff_behavior (input D, input CLK, output reg Q); 
    always @ (posedge CLK)
        Q <= D;
endmodule

2. Mealy 有限状态机和 Moore 有限状态机

下面两张图给出了两种常用状态机的结构，主要由三部分构成。图中的“当前状态时序逻辑”是存储当前状态的 \(n\) 个触发器，可用于表达 \(2^n\) 种状态。状态机中的所有触发器都由一个公共的时钟信号驱动，在时钟信号的触发沿（上升沿或下降沿）上改变其状态。状态机状态（即触发器的值）由“下一状态转移组合逻辑 \(F\)"的输出决定，该组合逻辑 \(F\) 接收当前状态和当前输入作为状态转移判断。电路输出由“输出组合逻辑 \(G\)”来决定，根据该组合逻辑 \(G\)​​ 是否接收输入信号，可以将状态机分为 Mealy 机 和 Moore 机 两种，分别如下图所示。

Mealy 有限状态机：

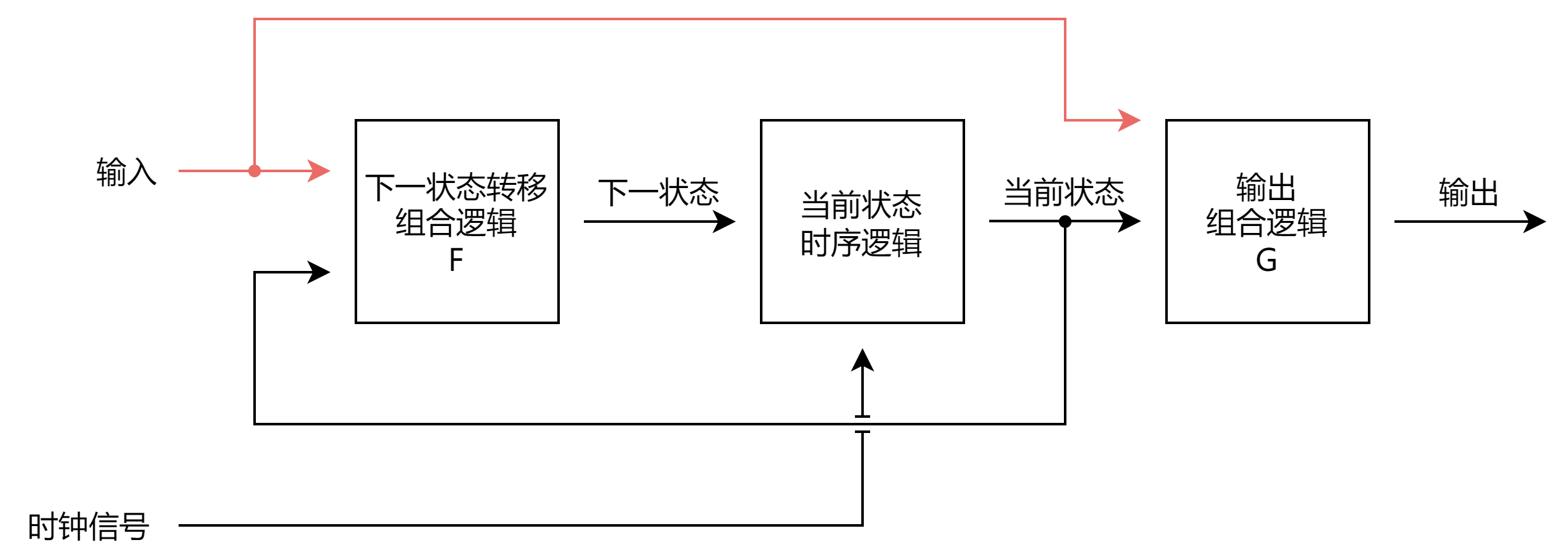
Moore 有限状态机：

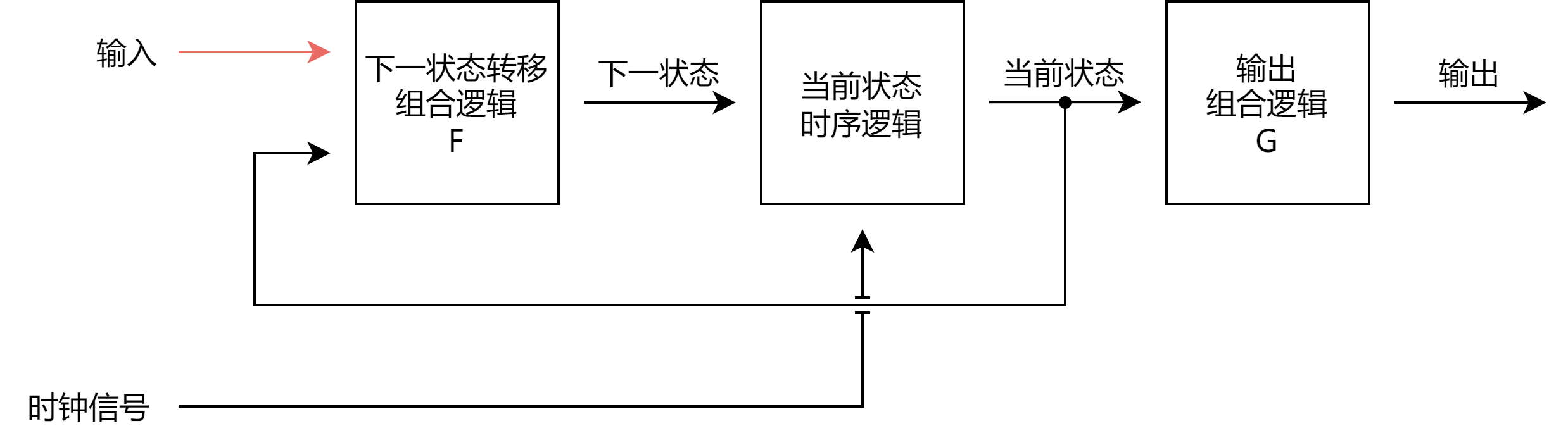
Mealy 机和 Moore 机拥有各自的优缺点，在实际的电路设计中都有可能被使用。由于 Mealy 机可以由当前输入直接得到输出结果而不经过状态转换，因此在实现相同功能时，Mealy 机可以比 Moore 机少一个状态，而且 Mealy 机的输出可以比 Moore 机提前一个时钟周期。但由于 Mealy 机的输出可能由当前输入得出，因此系统的输出容易受到输入信号中的毛刺影响，如果系统不能承受这种影响，则应使用 Moore 机。

我们通过一个例子来更深入地理解 Mealy 机和 Moore 机的异同。下图是一个 Mealy 机的状态图，该状态机的作用是将输入的二进制序列转换为补码，先输入的是最低有效位。状态图中，每个节点对应着一个状态，每条有向边表示一个状态转移。由于 Mealy 机的输出是当前状态和输入的函数，因此 Mealy 机的输出被标注在每一条有向边上。

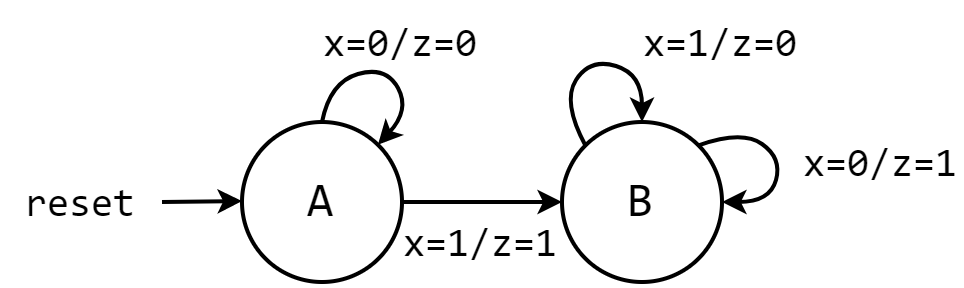
其对应的 Verilog 代码是：

module top_mealy (input clk, input reset, input x, output z); 
    parameter A = 2'b01;
    parameter B = 2'b10;

    reg [1:0] next_state;
    reg [1:0] state;

    // comb logic to generate next state
    always @(state, x) begin
        case (state)
            A: next_state = x ? B : A;
            B: next_state = B;
            default: next_state = A;
        endcase
    end

    // seq logic to generate current state
    always @(posedge clk or posedge reset) begin
        if (reset)
            state <= A;
        else
            state <= next_state;
    end

    // comb logic to generate output
    reg output_z;
    always @(state, x) begin
        case (state)
            A: output_z = x ? 1 : 0;
            B: output_z = x ? 0 : 1;
            default: output_z = 1'b0;
        endcase
    end
    assign z = output_z;

endmodule

如果使用 Moore 机来实现相同的功能，则需要新增一个中间状态，其状态图如下图所示。由于 Moore 机的输出与输入无关，仅由状态机当前的状态决定，因此 Moore 机的输出被标注在每一个节点上。

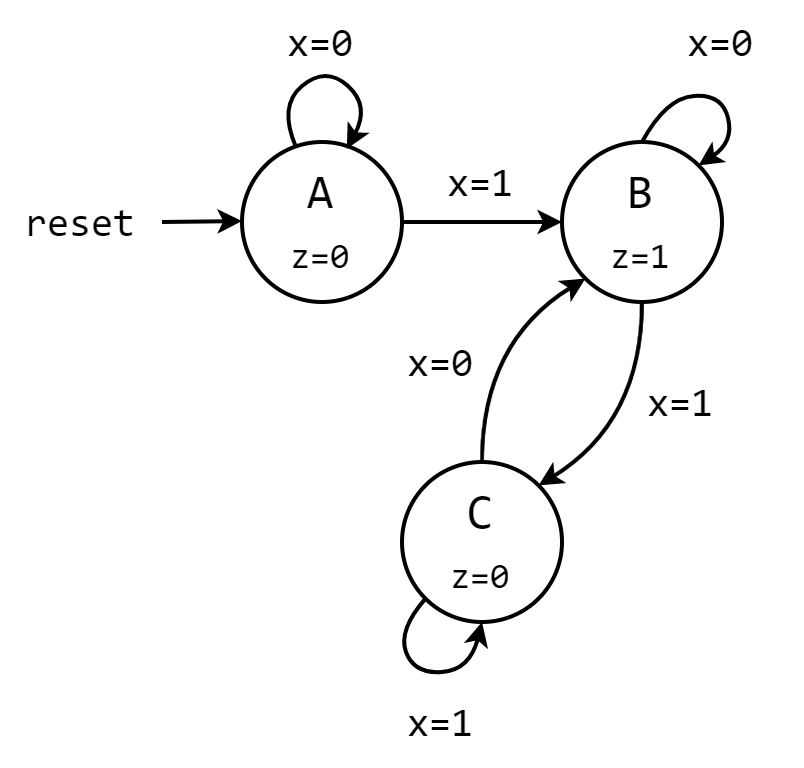
其对应的 Verilog 代码是：

module top_moore (input clk, input reset, input x, output z); 
    parameter A = 3'b001;
    parameter B = 3'b010;
    parameter C = 3'b100;
    
    reg [2:0] next_state;
    reg [2:0] state;

    // comb logic to generate next state
    always @(state, x) begin
        case (state)
            A: next_state = x ? B : A;
            B: next_state = x ? C : B;
            C: next_state = x ? C : B;
            default: next_state = A;
        endcase
    end

    // seq logic to generate current state
    always @(posedge clk or posedge reset) begin
        if (reset)
            state <= A;
        else
            state <= next_state;
    end

    // comb logic to generate output
    assign z = (state == B) ? 1 : 0;

endmodule

3. 状态机的两段式和三段式写法

在上一节中我们已经初步学习了使用 Verilog 表示状态机的方法，即使用一个 always 块表示当前状态的时序逻辑，使用两个 always 块表示下一状态转移的组合逻辑 \(F\) 与输出的组合逻辑 \(G\)。这种实现方法被称作状态机的两段式写法，即触发器分割了两部分的组合逻辑，电路的时序路径较短，可以获得更高的性能。由于两段式写法的输出由组合逻辑给出，因此输出信号可能存在毛刺。为了解决这个问题，可以使用三段式写法实现状态机。

在状态机的三段式写法中，输出端会增加一级触发器一滤除输出组合逻辑 \(G\) 可能产生的毛刺信号，而且输出组合逻辑 \(G\) 是根据下一状态来对输出做出判断，这样做不会消耗多余的时钟周期。如图所示为 Moore 机的三段式写法的结构图。

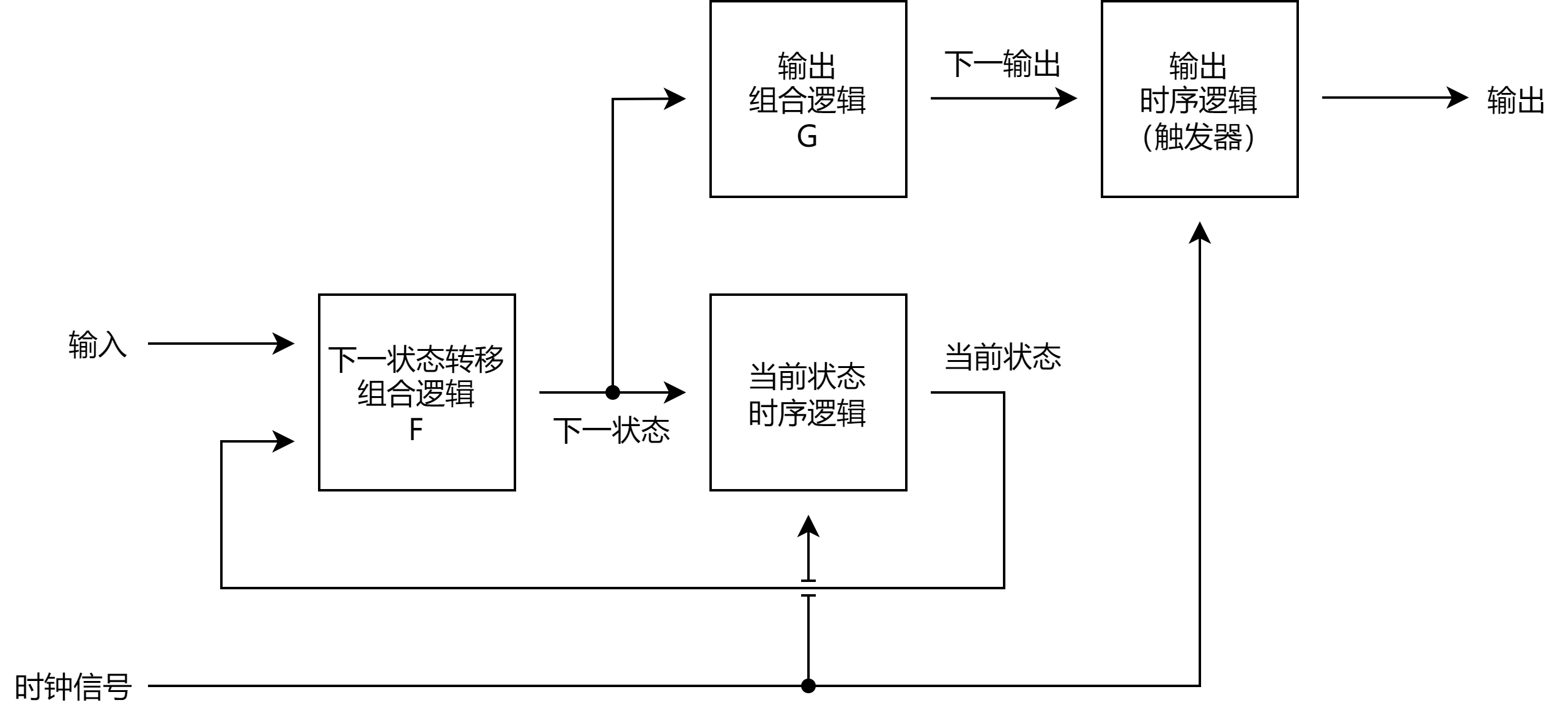
根据上述三段式 Moore 状态机的结构图，重写上节例子中 Moore 状态机的 Verilog 代码为三段式写法：

module top_moore (input clk, input reset, input x, output z); 
    parameter A = 3'b001;
    parameter B = 3'b010;
    parameter C = 3'b100;

    reg [2:0] next_state;
    reg [2:0] state;

    // comb logic to generate next state
    always @(state, x) begin
        case (state)
            A: next_state = x ? B : A;
            B: next_state = x ? C : B;
            C: next_state = x ? C : B;
            default: next_state = A;
        endcase
    end

    // seq logic to generate current state
    always @(posedge clk or posedge reset) begin
        if (reset)
            state <= A;
        else
            state <= next_state;
    end

    // seq logic to generate output
    reg output_z;
    always @(posedge clk or posedge reset) begin
        if (reset)
            output_z <= 1'b0;
        else
            output_z <= (next_state == B) ? 1 : 0;
    end
    assign z = output_z;

endmodule

那么 Mealy 机是否有相应的三段式写法呢？由于 Mealy 机的输出可能由当前输入得出，而输出的时序逻辑并不能得到下一输入，因此为了保证功能的正确性，必须在输出的时序逻辑后再增加一个组合逻辑 \(H\)，以根据当前的输入计算输出。如图所示为 Mealy 机的三段式写法的结构图。

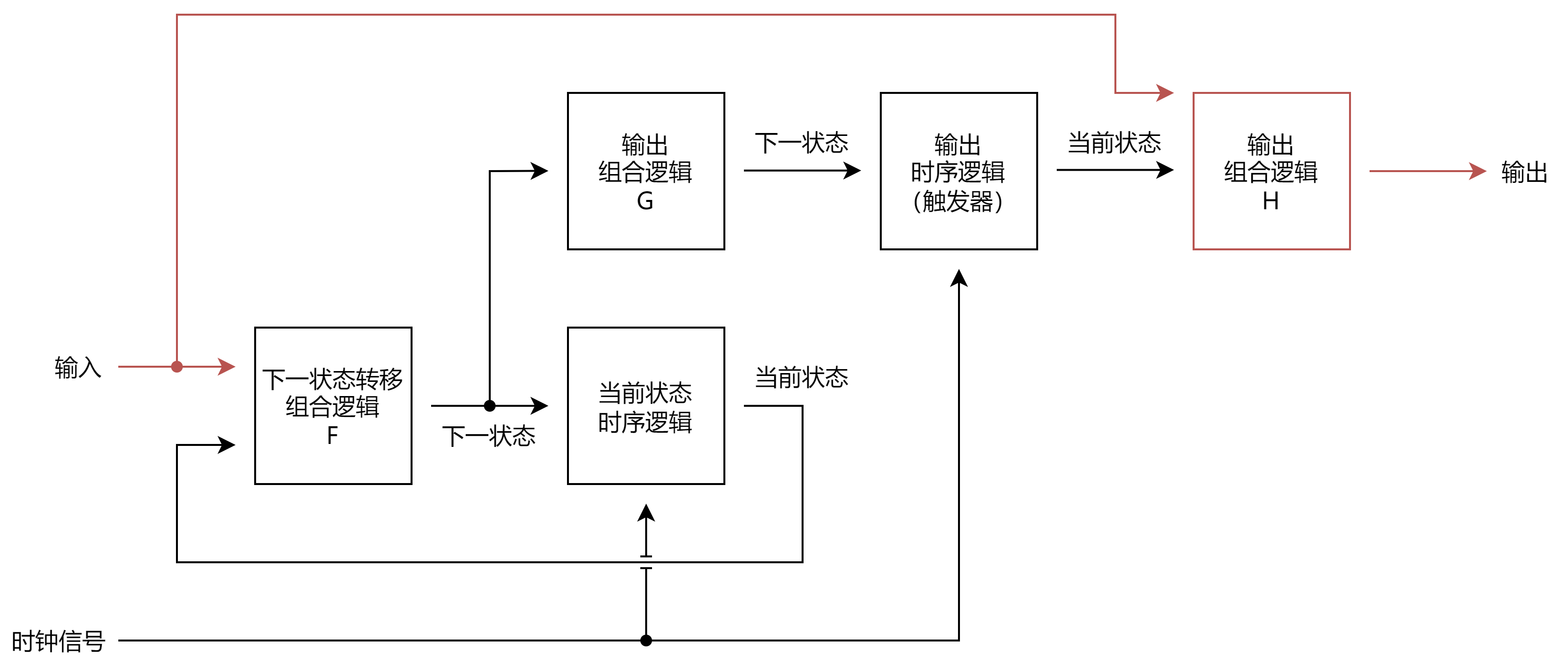
然而，这么做显然是与三段式写法的初衷相违背：状态机的输出仍然是组合逻辑驱动的，依然存在产生信号毛刺的可能。因此，三段式写法一般仅适用于 Moore 机。