数据结构 - AVL 树 AVL Tree

在计算机科学中，二叉搜索树（BST）是常用的数据结构，能够高效地支持动态数据的插入、删除和查询。然而，普通的二叉搜索树在数据分布不均的情况下可能退化为链表，从而导致操作效率下降到 \(O(n)\)。为了解决这一问题，1962 年两位苏联科学家 Adelson-Velsky 和 Landis 提出了第一种自平衡二叉搜索树——AVL 树。

AVL 树是一种经过改进的二叉搜索树，能够自动保持树的高度平衡，确保所有操作的时间复杂度为 \(O(\log{n})\)。本文将深入探讨 AVL 树的核心概念、操作方法及其实现。

1. 什么是 AVL 树

AVL 树是一种特殊的二叉搜索树，其关键特性是：

• 对于任意节点，其左右子树的高度差（平衡因子）不超过 1。
• 通过插入或删除节点后执行旋转操作，AVL 树能够自动维持平衡。

这种高度平衡的结构保证了 AVL 树的高度始终在 \(O(\log{n})\)，从而确保了高效的增删查操作。

1.1 平衡因子

平衡因子（Balance Factor）表示一个节点的左子树高度与右子树高度之差，即：

\[\text{Balance Factor} = \text{Height(Left Subtree)} - \text{Height(Right Subtree)} \]

• AVL树要求平衡因子必须在 {-1, 0, 1} 之间；
• 如果某个节点的平衡因子超出范围，则需要通过旋转操作恢复平衡。

2. AVL 树的基本操作

2.1 插入操作

插入节点后可能会破坏树的平衡性，此时需要通过旋转恢复平衡。插入后的平衡调整分为四种情况：

• 左左失衡（LL）： 在左子树的左侧插入节点，需要通过一次右旋恢复平衡。
• 右右失衡（RR）： 在右子树的右侧插入节点，需要通过一次左旋恢复平衡。
• 左右失衡（LR）： 在左子树的右侧插入节点，需要通过先左旋后右旋来恢复平衡。
• 右左失衡（RL）： 在右子树的左侧插入节点，需要通过先右旋后左旋来恢复平衡。

旋转操作本质上是调整子树结构，重新分配节点位置，从而恢复平衡。

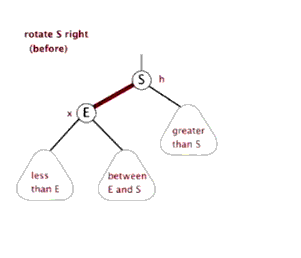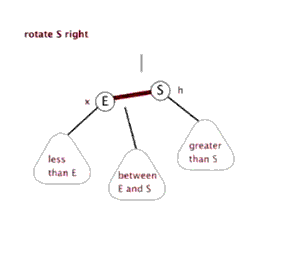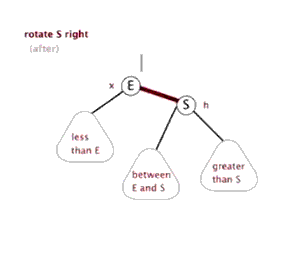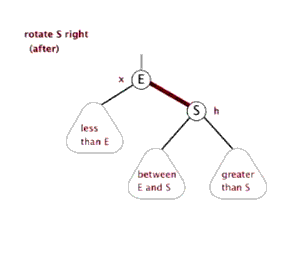
2.1.1 右旋

由于在左子树的左侧插入节点，使得左子树的高度比右子树大 2，形成 LL 失衡，因此需要通过右旋来恢复树的平衡。右旋操作主要分为两步：

• 根节点 S 的左孩子 E 变为新的根节点，S 变为 E 的右孩子；
• 原左孩子 E 的右子树变为原根节点 S 的左子树。

Node* rightRotate(Node* n) {
    Node* lnode = n->left;
    Node* rnode = n->right;
    
    lnode->right = n;
    n->left = rnode;
    
    updateHeight(n);
    updateheight(lnode);
    
    return lnode;
}

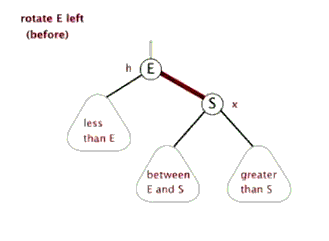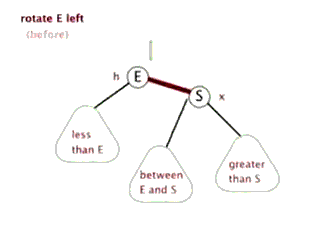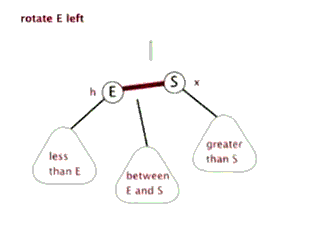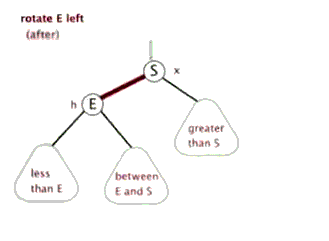
2.1.2 左旋

由于在右子树的右侧插入节点，使得右子树的高度比左子树大 2，形成 RR 失衡，因此需要通过左旋来恢复树的平衡。左旋操作主要分为两步：

• 根节点 E 的右孩子 S 作为新的根节点，E 变为 S 的左孩子；
• 原右孩子 S 的左子树变为原根节点 E 的右子树。

Node* leftRotate(Node* n) {
    Node* lnode = n->left;
    Node* rnode = n->right;
    
    rnode->left = n;
    n->right = lnode;
    
    updateHeight(n);
    updateHeight(rnode);
    
    return rnode;
}

2.1.3 先左旋后右旋

由于在左子树的右侧插入节点，使得左子树的高度比右子树大 2，形成 LR 失衡，并且单次的右旋并不能保证树的平衡，因此需要先左旋后右旋来维持平衡：即先对根节点的左子树进行左旋操作，再对根节点执行右旋操作，以达到平衡。

2.1.4 先右旋后左旋

由于在右子树的左侧插入节点，使得右子树的高度比左子树大2，形成 RL 失衡，并且单次的左旋并不能保证树的平衡，因此需要先右旋后左旋来维持平衡：即先对根节点的右子树进行右旋操作，再对根节点执行左旋操作，以达到平衡。

2.1.5 插入节点

Node* insert(Node* node, int key) {
    if (!node) return new Node(key);

    if (key < node->key) {
        node->left = insert(node->left, key);
    } else if (key > node->key) {
        node->right = insert(node->right, key);
    } else {
        return node;
    }

    updateHeight(node);

    int balance = getBalanceFactor(node);

    // LL
    if (balance > 1 && key < node->left->key) {
        return rightRotate(node);
    }
    // RR
    if (balance < -1 && key > node->right->key) {
        return leftRotate(node);
    }
    // LR
    if (balance > 1 && key > node->left->key) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }
    // RL
    if (balance < -1 && key < node->right->key) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

2.2 查询操作

AVL 树的节点查找操作与二叉搜索树一致。

void inorder(Node* node) {
    if (!node)
        return;
    inorder(node->left);
   	std::cout << node->key << " ";
    inorder(node->right);
}

3. AVL 树的复杂度分析

• 时间复杂度：AVL 树的建树时间复杂度为 \(O(n)\)；由于树的高度始终保持在 \(O(\log{n})\)，查找、插入、删除节点的时间复杂度都是 \(O(\log{n})\)。
• 空间复杂度：\(O(n)\)。

4. AVL 树的模板

struct Node {
    int key;
    int height;
    Node* left;
    Node* right;

    Node(int val) : key(val), height(1), left(nullptr), right(nullptr) {}
};

int getHeight(Node* node) {
    return node ? node->height : 0;
}

void updateHeight(Node* node) {
    node->height = 1 + max(getHeight(node->left), getHeight(node->right));
}

int getBalanceFactor(Node* node) {
    return node ? getHeight(node->left) - getHeight(node->right) : 0;
}

Node* rightRotate(Node* n) {
    Node* lnode = n->left;
    Node* rnode = n->right;
    
    lnode->right = n;
    n->left = rnode;
    
    updateHeight(n);
    updateheight(lnode);
    
    return lnode;
}

Node* leftRotate(Node* n) {
    Node* lnode = n->left;
    Node* rnode = n->right;
    
    rnode->left = n;
    n->right = lnode;
    
    updateHeight(n);
    updateHeight(rnode);
    
    return rnode;
}

Node* insert(Node* node, int key) {
    if (!node) return new Node(key);

    if (key < node->key) {
        node->left = insert(node->left, key);
    } else if (key > node->key) {
        node->right = insert(node->right, key);
    } else {
        return node;
    }

    updateHeight(node);

    int balance = getBalanceFactor(node);

    // LL
    if (balance > 1 && key < node->left->key) {
        return rightRotate(node);
    }
    // RR
    if (balance < -1 && key > node->right->key) {
        return leftRotate(node);
    }
    // LR
    if (balance > 1 && key > node->left->key) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }
    // RL
    if (balance < -1 && key < node->right->key) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

void inorder(Node* node) {
    if (!node)
        return;
    inorder(node->left);
   	std::cout << node->key << " ";
    inorder(node->right);
}

5. AVL 树与其他二叉平衡树的对比

特性	AVL 树	红黑树	Treap 树	Splay 树
节点平衡	高度严格	较宽松	随机性	动态调整
查询性能	优秀	优秀	优秀	较差（非局部）
实现难度	较高	较低	中等	较低
应用场景	高敏感性操作	大规模索引	动态优先队列	局部频繁访问