| 这个作业属于哪个班级 | 数据结构-网络20 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 余智康 |
目录
0. 展示PTA总分
1. 本章学习总结
2. PTA实验作业
0.PTA得分截图
1.本周学习总结
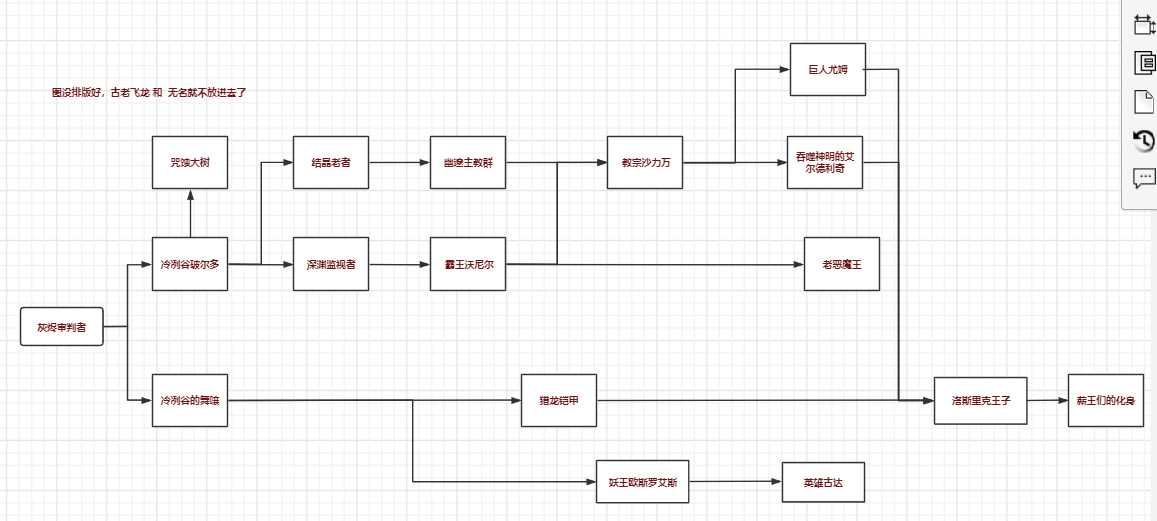
本次所有总结内容,请务必自己造一个图(不在教材或PPT出现的图),围绕这个图展开分析。建议:Python画图展示。图的结构尽量复杂,以便后续可以做最短路径、最小生成树的分析。
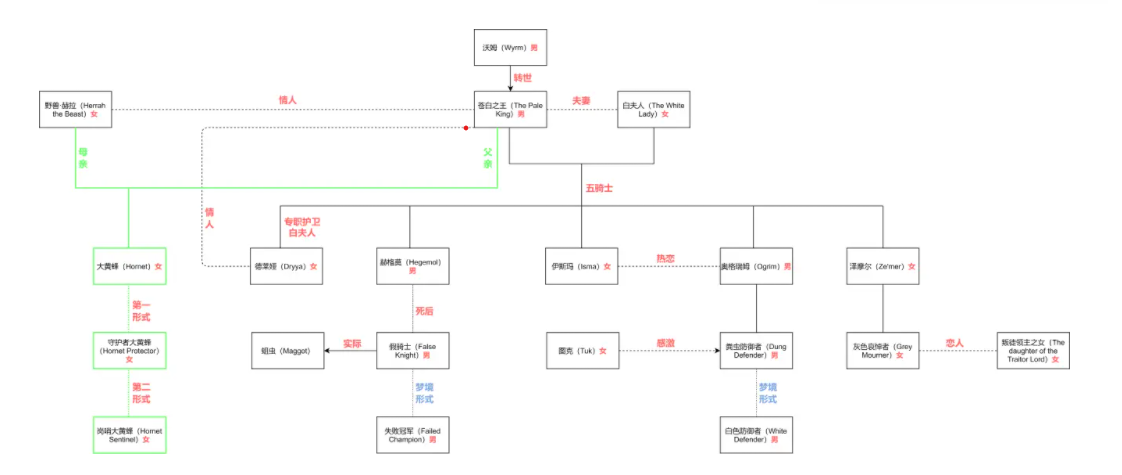
该图引自被B站 "《空洞骑士》:人物关系图谱",地址:https://www.bilibili.com/read/cv6403674/
修改后的关系图(部分):

1.1 图的存储结构
1.1.1 邻接矩阵
造一个图,展示其对应邻接矩阵
邻接矩阵的结构体定义
建图函数
- 结构体:
- 1)顶点的结构体:顶点编号、其它信息
- 2)图的结构体:二维数组(存放权值)、一维数组(存放顶点信息)、整型变量(存放顶点数、边数)
#define MAXV 100 //最大顶点数
typedef struct
{
int no; //顶点编号
InfoType info; //其它信息
}VertexType; //顶点结构体
typedef struct
{
int weight; //边
string relation; //关系
}EDGES;
typedef struct
{
EDGES edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数、边数
VertexType vexs[MAXV]; //存放顶点信息
}MatGraph; //图的结构图
-
存储:
- 以 “空洞骑士关系图(部分)” 为例
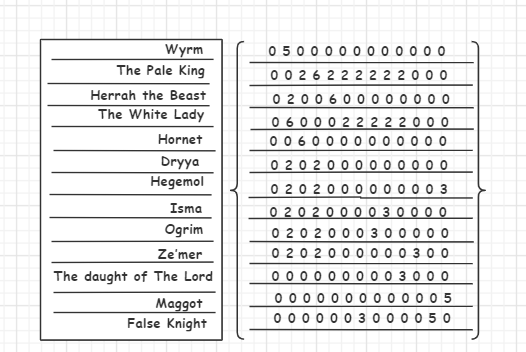
- 以 “空洞骑士关系图(部分)” 为例
-
申请空间:
1)因为0不使用,所以申请 node+1 个。
2)先给二级指针申请 node+1 个存放一级指针的空间,再 循环 给每一个一级指针申请 node+1个 存放结点数据的空间
g.edges = new EdgesType * [node+1];
for (i = 0; i <= node; i++)
{
g.edges[i] = new EdgesType[node+1];
}
- 建图(有向图):
- void CreatNode(),输入结点的信息:编号、名称,存放在 g.vexs[]数组中
- void CreatMGraph(),
1)创建邻接矩阵 :①邻接矩阵初始化 -> ②输入结点编号,(输入权值),修改对应位置的权值 -> ③ g.e = e, g.n = n;
1)建邻接矩阵的循坏条件,for i = 0 to e-1
void CreatNode(MGraph &g, int n) //输入结点信息
{
int No;
for(int i=1; i<=n; i++)
{
cin >> No;
g.vexs[No].no = No;
cin >> g.vexs[No].info;
}
}
void CreatMGraph(MGraph &g, int n, int e)
{
int i,j; //循环计数变量
int a,b;
//二维数组初始化
for(i=0; i<=n; i++)
for(j=0; j<=n; j++)
g.edges[i][j] = 0;
for(i=0; i<e; i++)
{
cin >>a >>b ;
cin >>g.edges[a][b].relation >>g.edges[a][b].weight;
}
g.n = n;
g.e = e;
}
1.1.2 邻接表
造一个图,展示其对应邻接表(不用PPT上的图)
邻接矩阵的结构体定义
建图函数
-
存储:
- 以 “空洞骑士关系图(部分)” 为例

- 以 “空洞骑士关系图(部分)” 为例
-
结构体:
typedef string InfoType,Vertex;
typedef struct ANode //边的结构体
{
int adjvex; //终点编号
struct ANode *nextarc; //下一条边的指针
InfoType info; //该边信息
double weight; //该边权值
}ArcNode;
typedef struct Vnode //结点的结构体
{
Vertex data; //顶点信息
ArcNode *firstarc; //第一条边
}VNode;
typedef struct
{
VNode adjlist[MAXV]; //邻接表
int n, e;
}AdjGraph;
- 建图:
void CreatAdj(AdjGraph *&G, int n, int e)
{
定义 p 为 指向ArcNode数据类型的指针
G = new AdjGraph G动态申请内存空间
for i=o to n do
G->adjlist[i].firstarc = NULL 初始化
end for
for i=0 to e-1 do
输入结点编号,a,b
p 申请内存空间,
p -> adjvex = b; b为终点编号
头插法将 p 插入 G->adjlist[a].fistarc
end for
G->n = n; G->e = e;
}
1.1.3 邻接矩阵和邻接表表示图的区别
各个结构适用什么图?时间复杂度的区别。
- 邻接矩阵:
- 适用于稠密图,稀疏图使用邻接矩阵会有较大的空间浪费
- 因为需要遍历二维数组,时间复杂度为 O(n^2)
- 邻接矩阵:
- 适用于稀疏图
- 时间复杂度为 O(n+e)
1.2 图遍历
1.2.1 深度优先遍历
选上述的图,继续介绍深度优先遍历结果
深度遍历代码
深度遍历适用哪些问题的求解。(可百度搜索)
-
"Wyrm"开始深度遍历结果:
- Wyrm(1) -> The Pale King(3) -> Herrah the Beast(2) -> Hornet(5) -> The White Lady(4) -> Dryya(6) -> Hegemol(7) -> False Knight(13) -> Maggot(12) -> Isma(8) -> Ogrim(9) -> Ze'mer(10) -> The daught of The Lord(11)
-
程序运行截图:

-
深度遍历代码:
void DFS(MGraph &g, int v)
{
if(v > g.n) return;
cout输出结点信息
visited[v] = 1; //标记为已读
while (未遍历完 v 的出度结点)
{
if 未访问过的结点 && 有权值 do
DFS(g, i) 进行递归
end if
移动到 v 的下一个出度结点
}
}
1.2.2 广度优先遍历
选上述的图,继续介绍广度优先遍历结果
广度遍历代码
广度遍历适用哪些问题的求解。(可百度搜索)
-
"Wyrm"开始广度遍历结果:
- Wyrm(1) -> The Pale King(3) -> Herrah the Beast(2) -> The White Lady(4) -> Hornet(5) -> Dryya(6) -> Heqemol(7) -> Isma(8) -> Ogrim(9) -> Ze'mer(10) -> False Knight(11) -> The daught of The Lord(13) -> Maggot(12)
-
程序运行截图:

-
广度遍历伪代码:
void BFS(MGraph g, int v)
{
if (v 结点没有出度 ) do 输出 v结点的信息 return
queue<int>que; //邻接表和临界矩阵中,队列类型均为 int型,之前邻接表犯过将其设为 ArcNode* 型的错误
v 入队列
记录 v 已经访问
while(队列不空)
{
取队头,赋值到 p中; 并出队;
cout 输出 p的信息
now 赋值为 p第一个出度结点(邻接表中ArcNode*)
while( p 的出度结点 未遍历 完) do
if 该出度结点未访问过 && 有权值 do
该结点 编号 入队列;并记录为已访问
end if
end while
}
}
- 问题的求解
-
- 只要找到问题的一种解决方式时,深度遍历比较快速,但不一定找到问题的最优解;
-
- 在问题存在多种解决方式时,广度遍历能给出全部可行的解决方案,可用于比较,从而选出最可能的解决方案;
-
- 深度遍历如本学期学习数据结构时,在线性表章节的迷宫寻路问题,一开始便是深度搜索找到一条路径;当不仅仅要找到走出迷宫的路径,还要比较多种路径,从而找出最短路径时,则使用了广度搜索。
-
1.3 最小生成树
用自己语言描述什么是最小生成树。
- 自己的语言解释最小生成树:
- 生成树:由图的 n 个顶点去掉多余的边由(n-1)条边连接的树。
- 最小生成树:权值之和最小的生成树
- 生成树是树,不是图,没有箭头。
1.3.1 Prim算法求最小生成树
基于上述图结构求Prim算法生成的最小生成树的边序列
实现Prim算法的2个辅助数组是什么?其作用是什么?Prim算法代码。
分析Prim算法时间复杂度,适用什么图结构,为什么?
-

-
Prim算法:
- Prim算法构造最小生成树的过程就是将右边圆圈中“候选区”的结点不断选中并放入左边矩形的“选中区”中;
-
辅助数组:
- lowcost[i]: lowcost也就是“候选区”,表示以i为出度的边的最小权值。当lowcost[i] = 0时,表示 i 结点已经加入到了最小生成树中;
- closet[i]: closet[i] 对应lowcost[i]的入度,则<closet[i],i>是最小生成树的一条边。其中 closet[i] = 0 表示以 i 结点作为树的根节点。
-
Prim算法操作:
-
初始化lowcost[], 其中lowcost[i]的值为v为入度,i为出度的权
值,权值为0 则置为INF(∞); -
初始化closet[],其中closet[i] = v。
-
从lowcost[]中找到最小的点 j ,进入最小生成树。并将 lowcost[j] = 0;
-
遍历顶点,若 weight<j,i>小于 lowcost[i] 则修改 lowcost[i],并修改closet[i]的入度为j。
-
循环3、4 总共进行 n-1 次,则n个顶点全部进入最小生成树;
- Prim代码:
void Prim(MGraph g, int v)
{
int* lowcost = new int[g.n + 1];
int* closet = new int[g.n + 1];
int min, node_min;
int i, k;
//1. 初始化lowcost[], 其中lowcost[i]的值为v为入度,i为出度的权值,权值为0 则置为INF(∞);
//2. 初始化closet[],其中closet[i] = v。
for (i = 0; i <= g.n; i++)
{
if (g.edges[v][i].weight != 0)
{
lowcost[i] = g.edges[v][i].weight;
}
else
{
lowcost[i] = INF;
}
closet[i] = v;
}
lowcost[v] = 0;
for (k = 0; k < g.n - 1; k++)
{
//3. 从lowcost[]中找到最小的点 j ,进入最小生成树。并将 lowcost[j] = 0;
min = INF;
for (i = 0; i <= g.n; i++)
{
if (lowcost[i] > 0 && lowcost[i] < min)
{
min = lowcost[i];
node_min = i;
}
}
lowcost[node_min] = 0;
cout << closet[node_min] << " and " << node_min << " weight-> " << min << endl;
//4. 遍历顶点,若 weight<j, i>小于 lowcost[i] 则修改 lowcost[i],并修改closet[i]的入度为j。
for (i = 0; i <= g.n; i++)
{
if (g.edges[node_min][i].weight != 0 && g.edges[node_min][i].weight < lowcost[i])
{
lowcost[i] = g.edges[node_min][i].weight;
closet[i] = node_min;
}
}
}
//5.循环3、4 总共进行 n - 1 次,则n个顶点全部进入最小生成树;
delete[] lowcost;
delete[] closet;
}
-
敲Prim代码时的 错误日志
- 错误一: 333 行 if (lowcost[i] != 0 && lowcost[i] < min) 误写为 if (lowcost[i] != 0 && min < lowcost[i])
- 错误二: 误将 330行的 min = INF放入 for循环中,导致找不到最小值
- 错误三: 339行、340行的 i 改为 node_min
- 错误四: 343行-351行的 for循环 内使用了未初始化的 j,改为node_min
- 错误五: 304、305行 new的空间 误写成 new lowcost = int[v+1],导致申请的空间不足,出错。改为new lowcost = int[g.n + 1]
- 错误六: 345行 if语句无需判断 lowcost[i] 是否为0, 改为判断 g.edges[node_min][i].weight 是否为0
- 错误七: 312行 lowcost[g.n]最后一个结点没有初始化
-
Prim算法得到的边序列
-
Prim时间复杂度:
- 两层for循环嵌套,时间复杂度 O(n^2)
-
Prim适用的图:
- 由于Prim算法和边数无关,执行的次数和顶点个数 n 有关,故比较适合稠密图。
1.3.2 Kruskal算法求解最小生成树
基于上述图结构求Kruskal算法生成的最小生成树的边序列
实现Kruskal算法的辅助数据结构是什么?其作用是什么?Kruskal算法代码。
分析Kruskal算法时间复杂度,适用什么图结构,为什么?
-
Kruskal算法:
- 1)ST 为空集
- 2)按边的权值 从小到大 放入边集 E 中
- 3)依次从 E 选择边放入 ST 中
- 3)筛选时,若所选择的边放入 ST 中构成了回路,则 舍弃 该边
- 4)返回步骤 3),直到 ST 中包含(n-1)条边
- 备注:工具树 并查集 同一个根 回路
-
辅助数组:
- 1)边集合 E,按权值 从小到大 存放边,E的结构体里的数据项: 初始顶点、终止顶点、边的权值
- 2)vset数组,用于并查集。存放每个结点的根,判断两个结点的根是否相同,从而判断是否在 同一个工具树 上,若在,则这两个结点会构成回路,舍弃该边。
-
Kruskal伪代码:
for i=0 to G.n do
vset[i] = i; //初始化
end for
for i=1 to G.n do
p = G.adjlist[i].firstacr;
while p!=NULL do
将 p 中的终点编号 和 权值 以及 i(起始结点编号)放入 E[]中
p = p-> nextarc;
end while
end for
调用函数,将 E[]排序
重置i,j未0
while i < G.n-1 do
取出 E[j]的结点编号,权值
检查两个结点是否存在于同一个集合
if vset[node_1] != vset[node_2]
for k=0 to G.n
修改集合编号
end for
输出
end if
end while
-
Kruskal算法得到的边序列
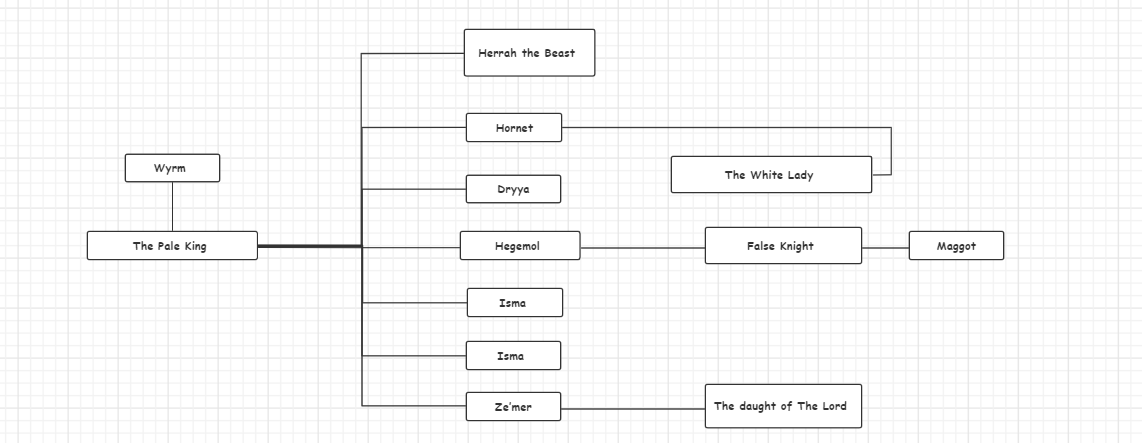
-
Kruskal时间复杂度:
- 上面那个的 Kruskal 代码的时间复杂度应该为 O(n^2)。
- 若将排序改为 堆排序,而且使用 并查集 ,则时间复杂度为 O(e log2 e)
-
Kruskal适用的图:
- Kruskal 算法的时间复杂度为 O(e log2 e),与图的结点数 n 无关,仅与边数 e 有关。则适合于稀疏图
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
基于上述图结构,求解某个顶点到其他顶点最短路径。(结合dist数组、path数组求解)
Dijkstra算法需要哪些辅助数据结构
Dijkstra算法如何解决贪心算法无法求最优解问题?展示算法中解决的代码。
Dijkstra算法的时间复杂度,使用什么图结构,为什么。
-
**基于上图,求 结点 “Wyrm(1)”到 “Ogrim(9)”的最短路径。(
图选的不成,这最短路径0.0)- Dijkstra:
- S 已经选入的点的集合; T 为选入点的集合;
- 1)若存在 <V0,vi>, 距离的值为<V0,Vi>弧上的权值;
- 2)若不存在,则距离为 INF(无穷);
- 3)从 T 中选择一个距离值最小的顶点W,加入 S;
- 4)在 W 加入 S 后,修改 T 中的距离值;
- 重复 3)4)直到 S 中包含所有顶点;
- Dijkstra:
-
辅助数组:
-
存放最短路径长度:一维数组 dist[],源点 v 默认
)其中dist[j] 表示源点 -> 顶点 j 的最短路径长度。
)dist[2]=12 表示源点 -> 顶点 2 的最短路径长度为12 -
存放最短路径:一维数组 path[]
) 一条最短路径用一个一维数组表示,如顶点1 -> 9的 最短路径为 1、3、9。表示为 path[] = {1,3,9}
)最短路径序列的前一项的顶点编号,无路径用 -1 表示
-
-
结果: Wyrm(1) -> The Pale King(3) -> Ogrim(9)
-
过程:
-
Dijkstra如何解决贪心算法的问题
- 通过修改 dist[]数组,使每次选中的结点到源点的距离均是最短;
- 代码:
for(j=0;j<g.n;j++)
{
if s[j] == 0
if g.edges[u][j] < INF && dist[u]+g.edges[u][j] < dist[j] do
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
- Dijkstra的时间复杂度,适合的图结构:
- 两层 for循环 嵌套, O(n^2)
- 适合 邻接矩阵 存储
- 备注:Dijkstra算法 不适用于带负数权值的带权图求最短;
—————不适用求最长路径:由于找到一个当前距离源点S最远的A点,则该段路径固定,但可能存在源点 S 到 B点,B点到A点,这两段加起来比 直接 S到A点更远。
1.4.2 Floyd算法求解最短路径
Floyd算法解决什么问题?
Floyd算法需要哪些辅助数据结构
Floyd算法优势,举例说明。
最短路径算法还有其他算法,可以自行百度搜索,并和教材算法比较。
-
Floyd算法的辅助数组:
- 二维数组 A 存放当前顶点之间的最短路径长度,如 A[i][j]表示当前顶点i到顶点j的最短路径长度
- 完了这个蛤子Floyd看不懂,来不及了,来不及了,这个就放着吧(;′⌒`)
-
Floyd算法解决哪些问题:
-
Floyd算法的优势:
-
其它最短路径的算法:
1.5 拓扑排序(
找一个有向图,并求其对要的拓扑排序序列
实现拓扑排序代码,结构体如何设计?
书写拓扑排序伪代码,介绍拓扑排序如何删除入度为0的结点?
如何用拓扑排序代码检查一个有向图是否有环路?
-
找一个有向图,并求其对要的拓扑排序序列
-
拓扑排序序列:
- 1)有向图中删去一个 没有前驱 的顶点,输出;
- 2)删去 以该顶点为 尾 的弧;
- 3)重复 1)2)直至 图空 ,或 图不空但找不到无前驱顶点 为止
- 备注: 若图不空 但找不到无前驱顶点,则是 存在环
-
上图 拓扑排序 结果:
-
拓扑排序结构体:
- !表头结点增加了 顶点入度的数据项
typedef struct
{
vertex data; //顶点信息
int count; //入度
ArcNode* firstarc; //第一条弧
}VexNode;
- 拓扑排序伪代码:
遍历邻接表
计算每个顶点的入度,存放在 表头结点的 count 中
遍历图顶点
将 入度为0 的顶点,入栈, 删除该结点
while 栈不空 do
出栈,v 结点 p = G->adjlist[v].firstarc
while p != NULL do
v 所有邻接点的入度 -1;
若 此时 入度为0 则入栈, 并在图中删去该结点
p = p->nextarc;
end while
end while
-
拓扑排序删去结点:
- 类似链表的删除操作
- 1)先判断 v 结点的第一条弧是否为空
- 2)判断第一个邻接点 的入度在 -1后 是否为 0
- 2) ① 若 -1后入度为0,则将该邻接点入栈。 并修改表头结点的 firstarc 为 该邻接点的nextarc,再delete掉该邻接点。最后重复 2)直到第一个邻接点的入度不为 0 或是 第一个邻接点不存在
- 2) ② 若 -1后入度不为0,则 p = firstarc,以 while(!p->nextarc)为循环条件,if(G->adjlist[p->nextarc.adjvex].count == 0) 则 用 temp存放 p->nextarc, 再 p = p->nextarc->nextarc,最后delete temp
-
检查一个有向图是否有环路:
* 1)在拓扑排序时,把有向图的顶点 真正上删除 ,然后再拓扑排序完遍历一下,看看图是否为空。若图不为空,则有环。
* 1)或者,假的删除,将拓扑排序中删去的顶点的 count 项赋值为 -1.拓扑排序完,统计是否有结点的 count 项不为 -1,则有环
1.6 关键路径(
什么叫AOE-网?
什么是关键路径概念?
什么是关键活动?
-
AOE-网:
- AOE网 为带权值的有向无环图;
- 顶点 为事件或状态;
- 弧 为活动发生的先后关系;
- 权值 为活动持续的时间
- 起点 入度为 0 的顶点 (仅有一个)
- 终点 出度为 0 的顶点 (仅有一个)
-
关键路径概念:
- 关键路径 为源点到汇点的 最长 路径, -> 转变为图的最长路径问题
- 备注: 求图的最长路径 不能 使用求最短路径的 Dijkstra算法实现。
-
关键活动:
- 关键活动: 在关键路径上的活动 都是关键活动
- 关键活动不存在富余时间
2.PTA实验作业
2.1 六度空间
选一题,介绍伪代码,不要贴代码。请结合图形展开分析思路。
2.1.0 思路
- 计数,距离不超过6
- 遍历
- 层次遍历! 如树的层次遍历并输出高度, 队列!lastNode!
2.1.1 伪代码(贴代码,本题0分)
建图;
for i=1 to G->n do
//CountNode(G,6,i)用于依次求得 每个顶点距离6以内的顶点数,并返回
proportion = (double)CountNode(G, 6, i) * 1.0 / node * 100;
输出
end for
int CountNode(AdjGraph* G, int distance, int v)
v 入队列,并标记为已读,同时count++ //(每次有数据进入队列,则count++)
while 队列不空 do
取队头,出队
取队头 的第一条弧 // p = firstarc
while p 不为空
若p->No结点未访问过,入队列,已访问,count++
p移动到 p->nextarc
end while
end while
2.1.2 提交列表
2.1.3 本题知识点
- 图的层次遍历
- 层次遍历中使用 lastNode 确定距离
2.2 旅游规划
2.2.1 思路:
- 最短路径 -> Dijkstra算法 -> 邻接矩阵 -> 无向图还是有向图 (思考:先试用有向图)
- 相同距离 取费用最低 -> Dijkstra算法使用时遇到多个相同的路径长度,path用二维数组(思考:string是否有一维数组的数据类型,可否使用),dist使用二维数组,与path对应。同时新引入一维cost数组,用于比较费用 -> 得出适合路径。
- (思考:邻接矩阵的二维数组是否可以使用结构体,用来存放距离和花费)
2.2.1 伪代码(贴代码,本题0分)
伪代码为思路总结,不是简单翻译代码。
部分结构体
typedef struct
{
int dist;
int cost;
}DIST_COST;
typedef struct
{
DIST_COST** edges;
int n,e;
}MGraph;
建图
......
2.2.2 提交列表
2.2.3 本题知识点










 浙公网安备 33010602011771号
浙公网安备 33010602011771号