统计方法

概率

概率分布

• 概率：事件A的频率等于A发生次数与实验次数比率。当实验次数概率趋近于无穷，即为概率。
• 分布曲线：把事件\(A_1，A_2，A_3\)……变成变量\(X\)，\(x\) ~ \(P（x）\)即为分布曲线
• 密度曲线：\(F(x)=\int_{-\infty}^x P(x)dx\)表示\(P(X<x)\).
• 常用分布：正态分布,\(\chi^2\)分布，t分布，F分布

抽样分布

从中样本空间抽取n个样本{\(x_1,x_2,x_3……x_n\)}
\(E(\bar x)=E(\dfrac 1 n\sum_{i=1}^n x_i )=\dfrac 1 nE(x_i)=\mu\)
\(D(\bar x)=D(\dfrac 1 n\sum_{i=1}^n x_i )=\dfrac 1 {n^2}D(x_i)=\dfrac {\sigma^2} n\)
由中心极限定理可知:从\((\mu,\sigma^2)\)中抽取n个样本,当n足够大时,样本均值\(\bar x\)~\((\mu,\dfrac {\sigma^2} n)\)
(先记住这个结论)

统计推断

区间估计

由上可知,,当n足够大时,样本均值\(\bar x\)~\((\mu,\dfrac {\sigma^2} n)\)
但现实中,我们不可能获得足够大的样本

\(E(\bar x)=\mu\pm\epsilon,\epsilon为误差\)

也就是说在\(\mu\)在\(E(\bar x)\)的左右偏移
误差项\(\epsilon\)~\((0,\dfrac {\sigma^2} n)\),易知\(\bar\epsilon=0\)
标准化,\(\dfrac {\epsilon}{\sigma/\sqrt n}\)~N(0,1)

\(\epsilon\)越小,估计越准确
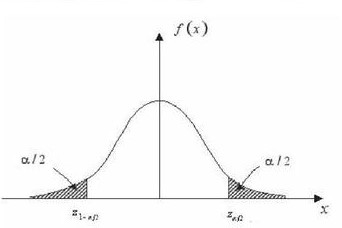
有\(1-\alpha%\)的概率落在白色区间,其中两边阴影部分的积分都为\(\alpha/2\),我们把\(1-\alpha%\)称为置信区间

假设\(F(x_1)=\alpha/2,F(x_2)=1-\alpha/2\)
所以\(x\)的取值区间为\(x_1到x_2\)
当\(X\)的分布为标准正态分布时,我们可以查表获得\(x_1,x_2\)的值.

我们获得置信区间下的\(\epsilon\)的区间\(\pm z_{\alpha/2}\dfrac{\sigma}{\sqrt n}\)后,
可以获得\(\mu\)的区间\(\bar x\pm z_{\alpha/2}\dfrac{\sigma}{\sqrt n}\)

总体方差的估计略

假设检验

假设检验和区间估计原理一样
区间估计是通过样本均值估计总体均值,加减可接受误差.如果要判断样本均值是否偏离预期,先求区间,再判断.
假设检验是先假设样本均值等于总体均值,如果误差可接受,假设成立.
\(z_{\alpha/2}\dfrac{\sigma}{\sqrt n}=\mu-\bar x\Longleftrightarrow z_{\alpha/2}=\dfrac{\mu-\bar x}{{\sigma}/{\sqrt n}}\)
如果\(z<z_{\alpha/2}\),假设成立

对于一定样本,这种判断可能会犯弃真错误\(\alpha\)错误,取伪错误\(\beta\)错误
\(\mu=\bar x\pm\epsilon\)
当误差偏态分布时,假设左偏,则左边取值会增加,取得错误值,左边取值会减少,放弃真值.

方差分析 (用到再补充)

是判断几组数据的相关性的方法
0|\(X_1\)|\(X_1\)|\(\dots\)|\(X_n\)
--|--|--|--|--|--
1|\(x_{11}\)|\(x_{21}\)||\(x_{n1}\)
\(\vdots\)|
n|

SST=SSA+SSE
SST=\(\sum_{i=1}^k\sum_{j=1}^{n_i}(x_{ij}-\bar{\bar x})^2\):总平方和
SSA=\(\sum_{i=1}^kn_i(\bar{x_i}-\bar{\bar x})^2\):组间平方和
SSE=\(\sum_{i=1}^k\sum_{j=1}^{n_i}(x_{ij}-\bar x)^2\):组内平方和
MSA=\(\dfrac {SSA} {k-1}\)
MSE=\(\dfrac {SSE} {n-k}\)

构建检验统计量F=\(\dfrac {MSA}{MSE}\)

P值