最优化简介

最优化简介

基本模型

\[\min f(x)\\ \text{s.t.} x \in \Omega \]

此问题相当于

\[-\max -f(x)\\ \text{s.t.} x \in \Omega \]

但有时会取不到最值，那样目标可变为上下确界，即

\[\inf f(x)\\ \text{s.t.} x \in \Omega \]

以及

\[-\sup -f(x)\\ \text{s.t.} x \in \Omega \]

• 全局最优点和局部最优点

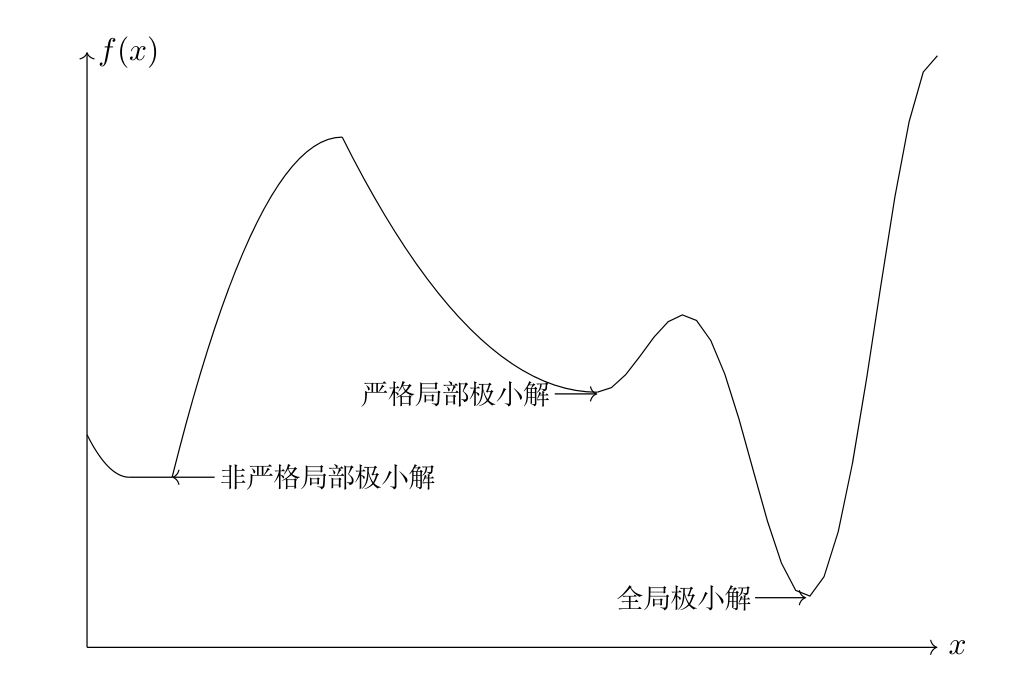
• 例：\(\min \frac{1}{2}\Vert Ax-b\Vert+ \tau\Vert x \Vert\)

• 迭代格式\(x^{k+1}=P_{\Omega}(x^k-\alpha _{k}\nabla f(x^k))\)

停机准则：

• \(\Vert x^{k+1}-x^{k}\Vert < \varepsilon\)
• \(|f(x_{k+1})-f(x_{k})| < \varepsilon\)

这两个都为绝对误差

• \((x-x^*)\nabla f(x^*) \geq 0,\quad \forall x \in\Omega\),自变量存在约束

算法涉及技巧

1.泰勒展开：（在某一点处用近似表达原函数）

例如：

\[\min f(x)+g(x) \]

邻近梯度方法所涉及思想，其中\(f(x)\)是光滑的，\(g(x)\)是非光滑的

• 邻近梯度方法：用一阶泰勒展开来代替光滑的\(f(x)\),并利用其一阶信息
• 牛顿法：二阶泰勒展开，涉及海瑟矩阵

2.对偶：

例：

\[\min f(x)\\ \text{s.t.}Ax=b \]

当\(f\)是凸函数，此时上述问题可以等价于

\[\min _x \max _{\lambda} f(x)-\lambda^T(Ax-b)\\ \iff \max _ \lambda (\min_x f(x)-\lambda^T(Ax-b)) \]

令\(g(x)=\min \limits_x f(x)-\lambda^T(Ax-b)\)

那么此问题可转化为

\[\max \limits_\lambda g(\lambda) \]

当\(A:m \times n,m\ll n\)，那么由对偶的方法可以使原问题降维，减少复杂度

3. 拆分

\[\min f(x)+g(x) \iff \min f(x)+g(y)\qquad \text{s.t. }y=x \]

\[\min f(x) \iff \min \frac{L}{2}\Vert x \Vert^2-(\frac{L}{2}\Vert x \Vert^2-f(x))\iff \min g(x)-h(x) \]

\(f\)满足\(\| \nabla f(x)-\nabla f(y)\| \leq L\|x-y\|\)，（即满足利普希兹条件），当\(g,f\)均为凸函数，此问题称为凸差规划

4. 块坐标下降法

\[\min f(x) \iff \min f(x_1,x_2,\dots,x_p),\quad x_i \in \mathbb R^{n_i},i=1,2,\dots p \]

其中\(f:\mathbb R ^n \to \mathbb R\)，且有\(n_1+n_2+\cdots+n_p =n\)

\[x_1^{k+1}=\arg \min f(x_1,x_2^k,\cdots,x_p^k)\\ x_2^{k+1}=\arg \min f(x_1^{k+1},x_2,\cdots,x_p^k)\\ \cdots \cdots\cdots\\ x_i^{k+1}=\arg \min f(x_1^{k+1},x_2^{k+1},\cdots,x_i,\dots x_p^k) \]

即为高斯-赛德迭代。

算法的收敛速度

• Q-收敛：

\[\frac{ \Vert x^{k+1}-x^*\Vert}{\|x^k-x^*\|}\leq a,a \in (0,1) \]

• Q-超线性收敛：

\[\lim _ {k\to \infty}\frac{ \Vert x^{k+1}-x^*\Vert}{\|x^k-x^*\|}=0 \]

• Q-次线性收敛：

\[\lim _ {k\to \infty}\frac{ \Vert x^{k+1}-x^*\Vert}{\|x^k-x^*\|}=1 \]

• Q-二次收敛：

  即对充分大的\(k\)有

\[\frac{ \Vert x^{k+1}-x^*\Vert}{\|x^k-x^*\|^2}\leq a,a >0 \]

• R-收敛速度(Root),若存在Q-线性收敛于0的非负序列\({t_k}\)，并且：

  \[\|x^k-x^*\|^2 \leq t_k \]

  其中\(t_k=a^k,a\in (0,1)\),则称\({x_k}\)是R-线性收敛

• 对函数值限制

\[f(x^k)-f(x^*)\leq\frac{c}{\sqrt k},c>0且为常数 \]

令\(\varepsilon=\frac{c}{\sqrt k},\)则\(k=\frac{c^2}{\varepsilon^2},\)规定误差\(\varepsilon\)，可计算迭代的次数\(k\).