Codeforces Deltix Round Spring 2021 [Div.1 + Div.2]
A. Game of Life
time limit per test: 1 second
memory limit per test: 256 megabytes
input: standard input
output: standard output
William really likes the cellular automaton called "Game of Life" so he decided to make his own version. For simplicity, William decided to define his cellular automaton on an array containing \(n\) cells, with each cell either being alive or dead.
Evolution of the array in William's cellular automaton occurs iteratively in the following way:
- If the element is dead and it has exactly 1 alive neighbor in the current state of the array, then on the next iteration it will become alive. For an element at index \(i\) the neighbors would be elements with indices \(i−1\) and \(i+1\). If there is no element at that index, it is considered to be a dead neighbor.
- William is a humane person so all alive elements stay alive.
Check the note section for examples of the evolution.
You are given some initial state of all elements and you need to help William find the state of the array after m iterations of evolution.
Input
Each test contains multiple test cases. The first line contains the number of test cases \(t (1\leqslant t\leqslant 10^{3})\). Description of the test cases follows.
The first line of each test case contains two integers \(n\) and \(m (2\leqslant n\leqslant 10^{3},1\leqslant m\leqslant 10^{9})\), which are the total number of cells in the array and the number of iterations.
The second line of each test case contains a string of length n made up of characters "0" and "1" and defines the initial state of the array. "1" means a cell is alive and "0" means it is dead.
It is guaranteed that the sum of n over all test cases does not exceed \(10^{4}\).
Output
In each test case output a string of length \(n\), made up of characters "0" and "1" — the state of the array after \(m\) iterations of evolution.
Example
input
4
11 3
01000000001
10 2
0110100101
5 2
10101
3 100
000
output
11111001111
1110111101
10101
000
Note
Sequence of iterations of evolution for the first test case
- 01000000001 — initial state
- 11100000011 — first iteration of evolution
- 11110000111 — second iteration of evolution
- 11111001111 — third iteration of evolution
Sequence of iterations of evolution for the second test case
- 0110100101 — initial state
- 1110111101 — first iteration of evolution
- 1110111101 — second iteration of evolution
Solution
逐个填即可,因为不会死掉。脑抽了一下,就写得比较长。
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <cstring>
#include <string>
#include <map>
#include <set>
#include <vector>
#include <list>
#include <queue>
using namespace std;
struct point {
int start, end;
} pnt;
int main()
{
int t;
int n;
int m;
char ch[1005];
vector<point> vt;
vector<vector<point>::iterator> vit;
int start, end;
scanf("%d", &t);
for (int i=0; i<t; i++) {
scanf("%d%d", &n, &m);
scanf("%s", ch);
vt.clear();
for (start=0; ch[start]=='0'; start++) ;
pnt.start = 0; pnt.end = start-1;
if (start > 0) vt.push_back(pnt);
while (start<n) {
while (start<n && ch[start]=='1') start++;
for (end=start; end<n && ch[end]=='0'; end++) ;
if (end > start) {
pnt.start = start;
pnt.end = end-1;
vt.push_back(pnt);
}
start = end;
}
for (vector<point>::iterator it=vt.begin(); it!=vt.end(); it++) {
int k;
if (it->start == 0 && it->end == n-1) continue;
if (it->start == 0 && it->end != n-1) {
k = min(m, it->end+1);
for (int i=0; i<k; i++) ch[it->end-i] = '1';
} else if (it->start != 0 && it->end == n-1) {
k = min(m, n-it->start);
for (int i=0; i<k; i++) ch[it->start+i] = '1';
} else {
k = min(m, (it->end-it->start+1)/2);
for (int i=0; i<k; i++) ch[it->start+i] = '1';
for (int i=0; i<k; i++) ch[it->end-i] = '1';
}
}
printf("%s\n", ch);
}
return 0;
}
B. Lord of the Values
time limit per test: 1 second
memory limit per test: 256 megabytes
input: standard input
output: standard output
While trading on his favorite exchange trader William realized that he found a vulnerability. Using this vulnerability he could change the values of certain internal variables to his advantage. To play around he decided to change the values of all internal variables from \(a_{1},a_{2},\cdots ,a_{n}\) to \(−a_{1},−a_{2},\cdots ,−a_{n}\) . For some unknown reason, the number of service variables is always an even number.
William understands that with his every action he attracts more and more attention from the exchange's security team, so the number of his actions must not exceed \(5000\) and after every operation no variable can have an absolute value greater than \(10^{18}\). William can perform actions of two types for two chosen variables with indices \(i\) and \(j\), where \(i<j\):
- Perform assignment \(a_{i}=a_{i}+a_{j}\)
- Perform assignment \(a_{j}=a_{j}−a_{i}\)
William wants you to develop a strategy that will get all the internal variables to the desired values.
Input
Each test contains multiple test cases. The first line contains the number of test cases \(t (1\leqslant t\leqslant 20)\). Description of the test cases follows.
The first line of each test case contains a single even integer \(n (2\leqslant n\leqslant 10^{3})\), which is the number of internal variables.
The second line of each test case contains \(n\) integers \(a_{1},a_{2},\cdots ,a_{n} (1\leqslant a_{i} \leqslant 10^{9})\), which are initial values of internal variables.
Output
For each test case print the answer in the following format:
The first line of output must contain the total number of actions \(k\), which the strategy will perform. Note that you do not have to minimize \(k\). The inequality \(k\leqslant 5000\) must be satisfied.
Each of the next \(k\) lines must contain actions formatted as "type i j", where "type" is equal to "1" if the strategy needs to perform an assignment of the first type and "2" if the strategy needs to perform an assignment of the second type. Note that \(i<j\) should hold.
We can show that an answer always exists.
Example
input
2
4
1 1 1 1
4
4 3 1 2
output
8
2 1 2
2 1 2
2 1 3
2 1 3
2 1 4
2 1 4
1 1 2
1 1 2
8
2 1 4
1 2 4
1 2 4
1 2 4
1 3 4
1 1 2
1 1 2
1 1 4
Note
For the first sample test case one possible sequence of operations is as follows:
- "2 1 2". Values of variables after performing the operation: [1, 0, 1, 1]
- "2 1 2". Values of variables after performing the operation: [1, -1, 1, 1]
- "2 1 3". Values of variables after performing the operation: [1, -1, 0, 1]
- "2 1 3". Values of variables after performing the operation: [1, -1, -1, 1]
- "2 1 4". Values of variables after performing the operation: [1, -1, -1, 0]
- "2 1 4". Values of variables after performing the operation: [1, -1, -1, -1]
- "1 1 2". Values of variables after performing the operation: [0, -1, -1, -1]
- "1 1 2". Values of variables after performing the operation: [-1, -1, -1, -1]
For the second sample test case one possible sequence of operations is as follows:
- "2 1 4". Values of variables after performing the operation: [4, 3, 1, -2]
- "1 2 4". Values of variables after performing the operation: [4, 1, 1, -2]
- "1 2 4". Values of variables after performing the operation: [4, -1, 1, -2]
- "1 2 4". Values of variables after performing the operation: [4, -3, 1, -2]
- "1 3 4". Values of variables after performing the operation: [4, -3, -1, -2]
- "1 1 2". Values of variables after performing the operation: [1, -3, -1, -2]
- "1 1 2". Values of variables after performing the operation: [-2, -3, -1, -2]
- "1 1 4". Values of variables after performing the operation: [-4, -3, -1, -2]
Solution
一个有趣的关注点是要求小于5000次操作,那么猜测两两进行操作一定可以在规定次数下实现两者分别取到负,验证可行。
不知道为啥注释掉的部分不能通过,我寻思着两个\(10^{9}\)数量级的数互相加减几次,中间变量怎么操作也不会超 \(10^{18}\) 吧。
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <cstring>
#include <string>
#include <map>
#include <set>
#include <vector>
#include <list>
#include <queue>
using namespace std;
int main()
{
int t;
int n;
int tmp;
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i=0; i<n; i++) scanf("%d", &tmp);
printf("%d\n", n*6/2);
for (int i=0; i<n; i+=2) {
/*printf("1 %d %d\n", i+1, i+2);
printf("2 %d %d\n", i+1, i+2);
printf("2 %d %d\n", i+1, i+2);
printf("1 %d %d\n", i+1, i+2);
printf("2 %d %d\n", i+1, i+2);*/
printf("2 %d %d\n", i+1, i+2);
printf("1 %d %d\n", i+1, i+2);
printf("2 %d %d\n", i+1, i+2);
printf("1 %d %d\n", i+1, i+2);
printf("2 %d %d\n", i+1, i+2);
printf("1 %d %d\n", i+1, i+2);
}
}
return 0;
}
C. Compression and Expansion
time limit per test: 2 seconds
memory limit per test: 256 megabytes
input: standard input
output: standard output
William is a huge fan of planning ahead. That is why he starts his morning routine by creating a nested list of upcoming errands.
A valid nested list is any list which can be created from a list with one item "1" by applying some operations. Each operation inserts a new item into the list, on a new line, just after one of existing items \(a_{1}.a_{2}.a_{3}\leqslant a_{k}\) and can be one of two types:
- Add an item \(a_{1}.a_{2}.a_{3}.\cdots.a_{k}.1\) (starting a list of a deeper level), or
- Add an item \(a_{1}.a_{2}.a_{3}.\cdots.(a_{k+1})\) (continuing the current level).
Operation can only be applied if the list does not contain two identical items afterwards. And also, if we consider every item as a sequence of numbers, then the sequence of items should always remain increasing in lexicographical order. Examples of valid and invalid lists that are shown in the picture can found in the "Notes" section.
When William decided to save a Word document with the list of his errands he accidentally hit a completely different keyboard shortcut from the "Ctrl-S" he wanted to hit. It's not known exactly what shortcut he pressed but after triggering it all items in the list were replaced by a single number: the last number originally written in the item number.
William wants you to help him restore a fitting original nested list.
Input
Each test contains multiple test cases. The first line contains the number of test cases \(t (1\leqslant t\leqslant 10)\). Description of the test cases follows.
The first line of each test case contains a single integer \(n (1\leqslant n\leqslant 10^{3})\), which is the number of lines in the list.
Each of the next n lines contains a single integer \(a_{i} (1\leqslant a_{i}\leqslant n)\), which is what remains of William's nested list.
It is guaranteed that in each test case at least one fitting list exists.
It is guaranteed that the sum of values n across all test cases does not exceed \(10^{3}\).
Output
For each test case output \(n\) lines which represent a valid nested list, which could become the data provided to you by William.
If there are multiple answers, print any.
Example
input
2
4
1
1
2
3
9
1
1
1
2
2
1
2
1
2
output
1
1.1
1.2
1.3
1
1.1
1.1.1
1.1.2
1.2
1.2.1
2
2.1
2.2
Note
In the second example test case one example of a fitting list is:
1
1.1
1.1.1
1.1.2
1.2
1.2.1
2
2.1
2.2
This list can be produced by using the sequence of operations shown below:
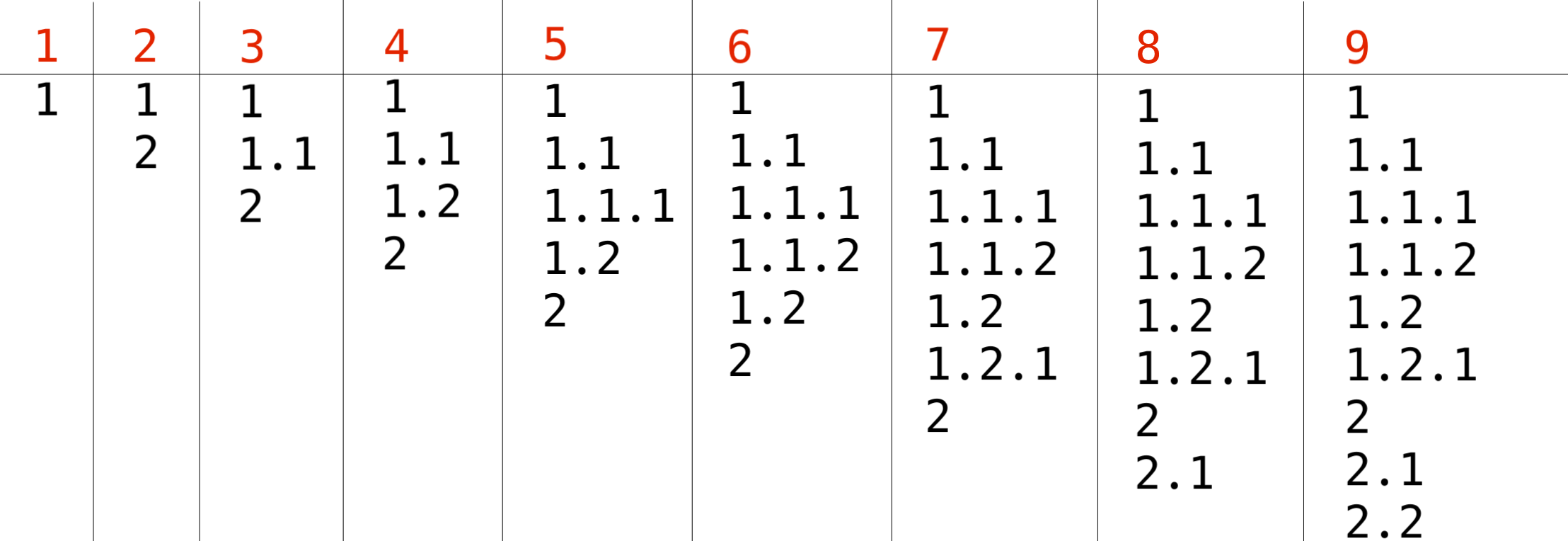
- Original list with a single item 1.
- Insert item 2 by using the insertion operation of the second type after item 1.
- Insert item 1.1 by using the insertion operation of the first type after item 1.
- Insert item 1.2 by using the insertion operation of the second type after item 1.1.
- Insert item 1.1.1 by using the insertion operation of the first type after item 1.1.
- Insert item 1.1.2 by using the insertion operation of the second type after item 1.1.1.
- Insert item 1.2.1 by using the insertion operation of the first type after item 1.2.
- Insert item 2.1 by using the insertion operation of the first type after item 2.
- Insert item 2.2 by using the insertion operation of the second type after item 2.1.
Solution
如果添加一个新的下级编号则一定是1;否则要么是继续编号,要么是小节结束,接续上级编号。
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <cstring>
#include <string>
#include <map>
#include <set>
#include <vector>
#include <list>
#include <queue>
using namespace std;
int main()
{
int t;
int n, tmp;
int sta[1005];
int pos = 0;
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
scanf("%d", &sta[0]);
pos = 0;
printf("%d\n", sta[0]);
for (int i=1; i<n; i++) {
scanf("%d", &tmp);
if (tmp == 1) {
sta[++pos] = tmp;
printf("%d", sta[0]);
for (int j=1; j<=pos; j++)
printf(".%d", sta[j]);
putchar('\n');
} else if (tmp == sta[pos]+1){
sta[pos] = tmp;
printf("%d", sta[0]);
for (int j=1; j<=pos; j++)
printf(".%d", sta[j]);
putchar('\n');
} else {
while (sta[pos]+1 != tmp) pos--;
sta[pos] = tmp;
printf("%d", sta[0]);
for (int j=1; j<=pos; j++)
printf(".%d", sta[j]);
putchar('\n');
}
}
}
return 0;
}
by SDUST weilinfox


 浙公网安备 33010602011771号
浙公网安备 33010602011771号