BVP问题
常见的 BVP 问题通常具有如下特点
- BVP是状态栅格采样算法(state sampled lattice planning)的基础。
- 没有通用的解,一般都是 case by case 的设计。
- 通常是一个复杂的数值优化问题。
Example
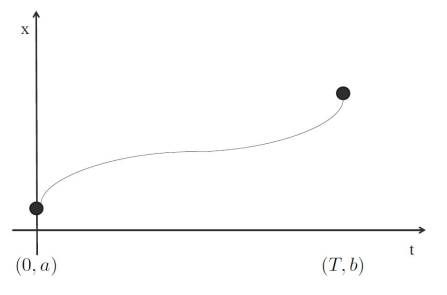
设计一个满足无人机动力学约束的轨迹 \(x(t)\) 满足如下约束:
当然这里我们只考虑了一个维度上的,无人机的三个维度可以分开进行考虑,轨迹如图所示:
我们通常使用一个多项式(polynominal)来表达一个轨迹,假设在这里使用一个五次多项式来模拟生成的轨迹(trajectory):
$$
x(t)=c_5t^5+c_4t^4+c_3t^3+c_2t^2+c_1t^1+c_0
$$
约束条件为:
|
Position |
Vecocity |
Acceleration |
| \(t=0\) |
\(a\) |
0 |
0 |
| \(t=T\) |
\(b\) |
0 |
0 |
然后求解如下方程即可:
\[\left[\begin{array}{l}
a \\
b \\
0 \\
0 \\
0 \\
0
\end{array}\right]=\left[\begin{array}{cccccc}
0 & 0 & 0 & 0 & 0 & 1 \\
T^{5} & T^{4} & T^{3} & T^{2} & T & 1 \\
0 & 0 & 0 & 0 & 1 & 0 \\
5 T^{4} & 4 T^{3} & 3 T^{2} & 2 T & 1 & 0 \\
0 & 0 & 0 & 2 & 0 & 0 \\
20 T^{3} & 12 T^{2} & 6 T & 2 & 0 & 0
\end{array}\right]\left[\begin{array}{l}
c_{5} \\
c_{4} \\
c_{3} \\
c_{2} \\
c_{1} \\
c_{0}
\end{array}\right]
\]
矩阵的第一行和第二行很容易得到,分别把 \(t=0\) 和 \(t=T\) 带入 \(x(t)\) 的多项式即可。但是后面的两行是怎么得到的呢?首先高中物理就知道位置的导数是速度,速度的导数是加速度,那么对 \(x(t)\) 的多项式进行两次求导,然后同样也是能知道其导数在 \(x=t\)和 \(x=T\) 时刻的值的,所以矩阵的后四行就是将这些值带入得到的。
但是如果上面的多项式是更高的次数时,我们所得到的解通常是无穷多个,此时哪个是最优解呢?我们不得而知,因此就引出了Optimal Boundary Value Problem (OBVP),即最优BVP问题的求解。
OBVP 问题
首先要对系统进行建模,构建出问题的一个代价函数(cost function),然后将其最小化求解即可。这里还是以无人机的模型为例子,我们要最小化无人机的控制变量在时间段 \(0-T\) 内的积分,即:
\[\begin{align}
J_{\Sigma}=\sum_{k=1}^{3} J_{k}, J_{k}=\frac{1}{T} \int_{0}^{T} j_{k}(t)^{2} dt \\
State: s_{k}=\left(p_{k}, v_{k}, a_{k}\right) \ \ Input: u_{k}=j_{k} \\
System model: \quad \dot{S}_{k}=f_{s}\left(s_{k}, u_{k}\right)=\left(v_{k}, a_{k}, j_{k}\right) \\
\end{align}
\]
如果我们在本案例中只考虑其中的一个轴的话,那么系统的方程就变成了
\[System model: \quad \dot{S}=f\left(s, u\right)=\left(v, a, j\right)
\]
其中 \(J_{\Sigma}=\sum_{k=1}^{3} J_{k}\) 表示的是三个轴的,但是在推导的时候暂时只先考虑一个轴,最终进行叠加即可。\(j_{k}(t)^{2}\) 即为系统的输入,这里我们把速度也当做了系统的状态变量,因此本系统中的输入为加加速度,通常成为 jerk, 而系统的状态变量主要包括了位置 \(p_k\),速度 \(v_k\) 和加速度 \(a_k\)。系统的一个状态方程则如上所示,在对系统状态求导之后就是 \((v,a,j)\),分别对应系统的三个状态变量。
系统的一个方程和损失函数知道后,下面就是求解了,在求解之前,我们首先来认识一下 Pontryain’s minimum principle,这里我们不对该定理的证明作任何的叙述,只要知道该定理能够帮助我们求解 OBVP 问题即可,看到该定理就直接 admit 它即可,Pontryain’s minimum principle 如下所示:
\[\dot{s}^{*}(t)=f\left(s^{*}(t), u^{*}(t)\right), \text { given }: s^{*}(0)=s(0)
\]
\(\lambda(t)\) 是下面微分方程的解,右侧表示的是 Hamiltonian 函数对状态变量各个分量的导数:
\[\dot{\lambda}(t)=-\nabla_{s} H\left(s^{*}(t), u^{*}(t), \lambda(t)\right)
\]
同时要满足或着说具有如下的界限条件:
\[\lambda(T)=-\nabla h\left(s^{*}(T)\right)
\]
最优的关于\(t\)的控制输入是:
\[u^{*}(t)=\arg \min _{u(t)} H\left(s^{*}(t), u(t), \lambda(t)\right)
\]
其中
- \(s^{*}\) 状态,关于时间 t 的最优的方程
- \(u^{*}\) 控制输入,关于时间 t 的最优的方程
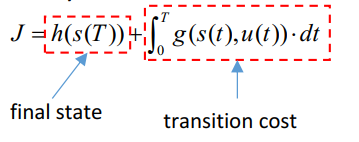
而一个通用的损失函数通常是具有如下形式的
分别解释一下 final state cost 和 transition cost
- final state
假设我们的无人机最终不强制一定要到达我们规定的目标点,允许有一些偏差,那么该项就存在,表示的是在无人机的运行过程中衡量距离目标点的一个代价函数。
- transition cost
假设我们有一个硬性约束,要求无人机一定要达到我们最终规定的点,那么该函数只有两个值,一个是当无人机到达该目标点的时候,函数值为0,另一个是当没有到达目标点的时候,函数值为无穷大,因此该函数此时是不可导的,我们也不将其纳入考虑范围内。
一个通用的 Hamiltonian 函数应该具有如下的形式:
\[\begin{aligned}
H(s, u, \lambda) & =g(s,u)+\lambda^{T} f_{s}(s, u) \\
\lambda & =(\lambda_{1},\lambda_{2},\lambda_{3} )
\end{aligned}
\]
根据 Pontryain 的最小原则,我们首先引入 costate:\(\lambda = \lambda_{1},\lambda_{2},\lambda_{3}\),因为我们暂时先只考虑一个轴,所以这里只有三个 \(lambda\),实际上根据我们上面的建模,系统的状态变量是有9个的,应该有9个 \(\lambda\),但是每个轴又都是独立的,因此可以分开证明考虑。
同时设计 Hamiltonian 函数:
\[\begin{aligned}
H(s, u, \lambda) & =\frac{1}{T} j^{2}+\lambda^{T} f_{s}(s, u) \\
& =\frac{1}{T} j^{2}+\lambda_{1} v+\lambda_{2} a+\lambda_{3} j
\end{aligned}
\]
从上到下只是进行了一个简单的展开,注意这里还是只考虑了单一的轴。
下面我们通过 Pontryain 的极小值原理进行求解,首先是根据 \(\lambda\) 的微分方程求解 \(\lambda\) 关于时间 \(t\) 的函数形式。定义微分方程中的 Hamiltonian 函数上面已经列出来了,下面求其对状态变量 \(s\) 的导数,\(s\) 中分别有三个分量,即 \((p,v,a)\),首先由于方程中没有 \(p\) 所以对 \(p\) 的导数为 \(0\),对 \(v\) 的导数为 \(\lambda_1\),对 \(a\) 的导数为 \(\lambda_2\)。
所以最终的微分方程是如下的形式:
$\lambda$关于$t$的微分方程的形式有了,下面就是对该方程求解了,第一项$(\lambda_1(t))$求导为 0,很明显是个常数,第二项$(\lambda_2(t))$求导为 $-\lambda_1$,第三项$(\lambda_3(t))$求导为的 $-\lambda_2$,那么我们就能写出关于 $\lambda$ 的最终形式了:
最终求得的关于 \(\lambda (t)\) 的形式如下所示,不过留心的同学可能会疑问为什么好像每一项都乘以了一个常数,确实是这样的,这里是为了方便后面的运算简单,至于这样会不会影响最终的结果呢,是不会的,因为我们是可以把例如 \(2a\) 看作一整个未知数进行求解的。
\[
\lambda(t)=\frac{1}{T}\left[\begin{array}{c}
-2 \alpha \\
2 \alpha t+2 \beta \\
-\alpha t^{2}-2 \beta t-2 \gamma
\end{array}\right]
\]
求出的最优输入关于时间 \(t\) 的方程如下所示,观察下式的第一行可以发现,此时系统状态 \(s\) 已经是最优的了,因此我们可以不用考虑式子中含有 s 分量的部分,即带有 \((p,v,a)\) 的部分都可以直接去掉,当做常数对待。此时的 H 函数则变成了:
\[\begin{aligned}
H (s^{*}(t),j(t),\lambda(t)) &= \frac{1}{T}j^2 + \lambda_{3}j + D \\
D &= \lambda_1v + \lambda_2a
\end{aligned}
\]
由于 \(\lambda_1,lambda_1\) 已知,上面求解出来的,且与 \(v,a\) 无关,所以 \(D\) 为常数。求该式关于 \(j\) 的最小值,直接对 \(j\) 求导让其等于\(0\)可得:
\[j(t)=-\frac{T}{2}\lambda_3
\]
再将 \(\lambda_3\) 带入即可得到如下结果
\[\begin{aligned}
u^{*}(t) & =j^{*}(t)=\arg \min _{j(t)} H\left(s^{*}(t), j(t), \lambda(t)\right) \\
& =\frac{1}{2} \alpha t^{2}+\beta t+\gamma
\end{aligned}
\]
同时 \(s\) 中的三个分量分别是导数关系,即 \(p\) 的导数 \(v\),\(v\) 的导数为 \(j\),这里和 \(u\) 表达的是同一个意思,一次可以通过 \(u\) 来分别求出 \(v,p\),如下所示:
\[s^{*}(t)=\left[\begin{array}{c}
\frac{\alpha}{120} t^{5}+\frac{\beta}{24} t^{4}+\frac{\gamma}{6} t^{3}+\frac{a_{0}}{2} t^{2}+v_{0} t+p_{0} \\
\frac{\alpha}{24} t^{4}+\frac{\beta}{6} t^{3}+\frac{\gamma}{2} t^{2}+a_{0} t+v_{0} \\
\frac{\alpha}{6} t^{3}+\frac{\beta}{2} t^{2}+\gamma t+a_{0}
\end{array}\right]
\]
其中初始状态:
\[\quad s(0)=\left(p_{0}, v_{0}, a_{0}\right)
\]
可以得到 cost(将求解得到的 \(j(t)\) 带入损失函数即可):
\[
J=\gamma^{2}+\beta \gamma T+\frac{1}{3} \beta^{2} T^{2}+\frac{1}{3} \alpha \gamma T^{2}+\frac{1}{4} \alpha \beta T^{3}+\frac{1}{20} \alpha^{2} T^{4}
\]
\(\alpha, \beta, \gamma\) Is solved as:
\[
\begin{array}{l}
{\left[\begin{array}{ccc}
\frac{1}{120} T^{5} & \frac{1}{24} T^{4} & \frac{1}{6} T^{3} \\
\frac{1}{24} T^{4} & \frac{1}{6} T^{3} & \frac{1}{2} T^{2} \\
\frac{1}{6} T^{3} & \frac{1}{2} T^{2} & T
\end{array}\right]\left[\begin{array}{l}
\alpha \\
\beta \\
\gamma
\end{array}\right]=\left[\begin{array}{c}
\Delta p \\
\Delta v \\
\Delta a
\end{array}\right]} \\
{\left[\begin{array}{c}
\Delta p \\
\Delta v \\
\Delta a
\end{array}\right]=\left[\begin{array}{c}
p_{f}-p_{0}-v_{0} T-\frac{1}{2} a_{0} T^{2} \\
v_{f}-v_{0}-a_{0} T \\
a_{f}-a_{0}
\end{array}\right]}
\end{array}
\]
\[
\left[\begin{array}{l}
\alpha \\
\beta \\
\gamma
\end{array}\right]=\frac{1}{T^{5}}\left[\begin{array}{ccc}
720 & -360 T & 60 T^{2} \\
-360 T & 168 T^{2} & -24 T^{3} \\
60 T^{2} & -24 T^{3} & 3 T^{4}
\end{array}\right]\left[\begin{array}{l}
\Delta p \\
\Delta v \\
\Delta a
\end{array}\right]
\]
This derivation holds for fixed final state: \(s(T)=\left(p_{f}, v_{f}, a_{f}\right)\)
Reference





 浙公网安备 33010602011771号
浙公网安备 33010602011771号