2022年6月练习
P5024 [NOIP2018 提高组] 保卫王国
一颗树有 \(n\) 个点 \((1 \le n \le 10^5)\) , 带点权 。
给出 \(m\) 个询问 \((1 \le m \le 10^5)\) ,对于每个询问 ,你需要在树上选若干个点,满足如下条件:
- 树上每一条边所连的两个节点中有至少一个被选中;
- 限制询问相关的两个点必须被选中或不被选中;
要求你回答在满足上述条件的前提下,所选点点权的和的最小值,若无法满足上述条件则输出 \(-1\) 。
第一眼:要是没有条件 2 ,这就是一个骡的极小点覆盖集,再加上有 \(10^5\) 个询问,所以必然要使用倍增(或树剖)预处理。
考虑先不顾条件 2 ,考虑每个子树的根节点是否选的情况,用深搜做一遍子树点权和的DP;(然后就不晓得做了,果断贺 TJ )
再进行一次深搜,处理出全树点权和减去当前子树点权和(同样也需考虑子树的根节点是否选的情况)
核心:随后处理出 \(ldp[u][g][0/1][0/1]\) ,意为节点 u 与距其 \(2^n\) 的祖先所构成的链与其上的子树的最小权值和(后两个下标为判断链的两端是否被选)
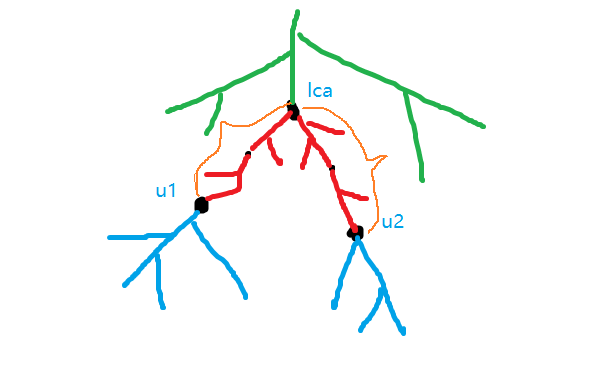
(如图,深搜第一次处理蓝色部分,第二次处理绿色部分,随后预处理链的情况,预计最多需 \(2 \log n\) 条小链构成图中红色的长链)
处理后分别解决每个询问,用 \(LCA\) 计算即可。时间复杂度 \(O(n \log n)\)
总结:这样的水体虽然是码农题,但是写一天实在是太过分了,要提高效率
code
#include <bits/stdc++.h>
#define ll long long
#define rgi register int
using namespace std;
const int M=1e5+7;
const int inf=1e11+7;
inline int read(){
int w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
void gitgud(){
int ans=0;
for(int i=1;i<=100;i++)ans++;
}
int n,m,p[M],tim;
int head[M],tot;
struct edge{
int pre,to;
}line[M*2];
struct qst{
int u1,s1,u2,s2;
}q[M];
void add(int fr,int tr){
line[++tot].pre=head[fr];
head[fr]=tot;
line[tot].to=tr;
}
int up[18][M],depp[M];
int dp[2][M];
int ddp[2][M],ldp[18][M][2][2];
//up:2^n辈祖先 dp:子树节点选不选费用 ddp:全树减子树节点选不选费用 ldp:链两端(包含链旁的子树)节点选不选费用(题解思路)
void dfs(int u,int fa){
dp[1][u]=p[u];
up[0][u]=fa;
depp[u]=depp[fa]+1;
for(int i=head[u];i;i=line[i].pre){
int kid=line[i].to;
if(kid==fa)continue;
dfs(kid,u);
dp[0][u]+=dp[1][kid];
dp[1][u]+=min(dp[0][kid],dp[1][kid]);
}
// printf("*%d %d %d %d\n",u,fa,dp[0][u],dp[1][u]);
}
void dfs2(int u,int fa){
for(int i=head[u];i;i=line[i].pre){
int kid=line[i].to;
if(kid==fa)continue;
ddp[0][kid]=ddp[1][u]+dp[1][u]-min(dp[0][kid],dp[1][kid]);
ddp[1][kid]=min(ddp[0][u]+dp[0][u]-dp[1][kid],ddp[0][kid]);
dfs2(kid,u);
}
}
void preLCA(){
for(int i=2;i<=n;i++){
ldp[0][i][0][0]=inf;
ldp[0][i][0][1]=dp[0][up[0][i]]-dp[1][i];
ldp[0][i][1][0]=dp[1][up[0][i]]-min(dp[0][i],dp[1][i]);
ldp[0][i][1][1]=ldp[0][i][1][0];
// printf("***ldp[0][%d][0][0]=%lld ldp[0][%d][0][1]=%lld ldp[0][%d][1][0]=%lld ldp[0][%d][1][1]=%lld\n",i,ldp[0][i][0][0],i,ldp[0][i][0][1],i,ldp[0][i][1][0],i,ldp[0][i][1][1]);
}
for(int i=1;i<18;i++){
for(int j=2;j<=n;j++){
up[i][j]=up[i-1][up[i-1][j]];
ldp[i][j][0][0]=min(ldp[i-1][up[i-1][j]][0][1]+ldp[i-1][j][1][0],ldp[i-1][up[i-1][j]][0][0]+ldp[i-1][j][0][0]);
ldp[i][j][0][1]=min(ldp[i-1][up[i-1][j]][0][1]+ldp[i-1][j][1][1],ldp[i-1][up[i-1][j]][0][0]+ldp[i-1][j][0][1]);
ldp[i][j][1][0]=min(ldp[i-1][up[i-1][j]][1][1]+ldp[i-1][j][1][0],ldp[i-1][up[i-1][j]][1][0]+ldp[i-1][j][0][0]);
ldp[i][j][1][1]=min(ldp[i-1][up[i-1][j]][1][1]+ldp[i-1][j][1][1],ldp[i-1][up[i-1][j]][1][0]+ldp[i-1][j][0][1]);
}
}
}
ll num1[2],num2[2],sta1[2],sta2[2];
ll LCA(int u1,int u2,int s1,int s2){
num1[0]=num1[1]=num2[0]=num2[1]=inf;
sta1[0]=sta1[1]=sta2[0]=sta2[1]=0;
if(depp[u1]>depp[u2])swap(u1,u2),swap(s1,s2);
num1[s1]=dp[s1][u1],num2[s2]=dp[s2][u2];
// printf("st:%d %d %d %d %lld %lld\n",u1,s1,u2,s2,num1[s1],num2[s2]);
for(int i=17;i>=0;i--){
if(depp[up[i][u2]]>=depp[u1]){
sta2[0]=min(ldp[i][u2][0][0]+num2[0],ldp[i][u2][0][1]+num2[1]);
sta2[1]=min(ldp[i][u2][1][0]+num2[0],ldp[i][u2][1][1]+num2[1]);
num2[0]=sta2[0],num2[1]=sta2[1];
u2=up[i][u2];
}
}
if(u1==u2)return ddp[s1][u1]+num2[s1];
for(int i=17;i>=0;i--)
if(up[i][u2]!=up[i][u1]){
sta1[0]=min(ldp[i][u1][0][0]+num1[0],ldp[i][u1][0][1]+num1[1]);
sta1[1]=min(ldp[i][u1][1][0]+num1[0],ldp[i][u1][1][1]+num1[1]);
num1[0]=sta1[0],num1[1]=sta1[1];
sta2[0]=min(ldp[i][u2][0][0]+num2[0],ldp[i][u2][0][1]+num2[1]);
sta2[1]=min(ldp[i][u2][1][0]+num2[0],ldp[i][u2][1][1]+num2[1]);
num2[0]=sta2[0],num2[1]=sta2[1];
u1=up[i][u1],u2=up[i][u2];
}
// printf("st:%d %d %d %d %lld %lld\n",u1,s1,u2,s2,num1[s1],num2[s2]);
int lca=up[0][u1];
int an1=dp[0][lca]-dp[1][u1]-dp[1][u2]+num1[1]+num2[1]+ddp[0][lca];
int an2=dp[1][lca]-min(dp[0][u1],dp[1][u1])+min(num1[0],num1[1])-min(dp[0][u2],dp[1][u2])+min(num2[0],num2[1])+ddp[1][lca];
// printf("ed:%d %d %d %lld %lld %lld %lld %lld %lld\n",lca,u1,u2,an1,an2,num1[0],num1[1],num2[0],num2[1]);
return max(an1,an2);
}
int main(){
// freopen("text.in","r",stdin);
// freopen("text.out","w",stdout);
n=read(),m=read(),read();
for(int i=1;i<=n;i++)p[i]=read();
for(int i=1;i<n;i++){
int fr=read(),tr=read();
add(fr,tr),add(tr,fr);
}
for(int i=1;i<=m;i++){
q[i]=(qst){read(),read(),read(),read()};
}
dfs(1,0);
dfs2(1,0);
preLCA();
for(int i=1;i<=m;i++){
tim=i;
int anss=LCA(q[i].u1,q[i].u2,q[i].s1,q[i].s2);
printf("%d\n",(anss>=inf)?-1:anss);
}
return 0;
}
/*
5 3 C3
2 4 1 3 9
1 5
5 2
5 3
3 4
1 0 3 0
2 1 3 1
1 0 5 0
别想直接复制
*/
「SNOI2017」炸弹
按照这篇博客中的思路,复杂度为 \(O(n)\) 。
code
#include <bits/stdc++.h>
#define ll long long
#define rgi register int
using namespace std;
const int M=5e5+7,inf=1e9+7,modd=1e9+7;
inline ll read(){
ll w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
void gitgud(){
int ans=0;
for(int i=1;i<=100;i++)ans++;
}
ll n,x[M],r[M],bl[M],br[M];
int main(){
gitgud();
n=read();
for(int i=1;i<=n;i++){
x[i]=read(),r[i]=read();
bl[i]=br[i]=i;
}
for(int i=2;i<=n;i++)while(bl[i]!=1&&x[i]-x[bl[i]-1]<=r[i]){
r[i]=max(r[i],x[bl[i]-1]+r[bl[i]-1]-x[i]);
bl[i]=bl[bl[i]-1];
}
for(int i=n-1;i;i--)while(br[i]!=n&&x[br[i]+1]-x[i]<=r[i]){
bl[i]=min(bl[i],bl[br[i]+1]);
br[i]=br[br[i]+1];
}
// for(int i=1;i<=n;i++)printf("**%lld %lld\n",bl[i],br[i]);
ll ans=0;
for(int i=1;i<=n;i++)ans=(ans+(ll)i*(br[i]-bl[i]+1)%modd)%modd;
printf("%lld\n",ans);
return 0;
}
/*
4
1 1
5 1
6 5
15 15
*/
P6794 [SNOI2020] 水池
同上。
code
P7113 [NOIP2020] 排水系统
DAG->拓扑序板子题
需要用__int128,否则只能得90pts
我__int128的输出写挂了,找了两个小时错误
code
#include <bits/stdc++.h>
#define ll long long
#define rgi register int
using namespace std;
const int M=2e5+7,inf=1e9+7,modd=1e9+7;
inline int read(){
int w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
void gitgud(){
int ans=0;
for(int i=1;i<=100;i++)ans++;
}
int n,q,w[M],tot,rt[M*70];
struct node{
int ls,rs,lzy;
int h,bl,br;//bl,br:区间内左板最大、右板最大
};
struct sgt{
node d[M*70];
void pushup(int u){
d[u].bl=max(d[d[u].ls].bl,d[d[u].rs].bl);
d[u].br=max(d[d[u].ls].br,d[d[u].rs].br);
}
int abuild(int u){
int ii=++tot;
d[ii]=d[u];
return ii;
}
void pushdown(int u){
if(d[u].lzy){
d[u].ls=abuild(d[u].ls),d[u].rs=abuild(d[u].rs);
d[d[u].ls].lzy=d[d[u].rs].lzy=d[u].lzy;
if(d[u].lzy==1){
d[d[u].ls].h=d[d[u].rs].h=d[u].h;
}else if(d[u].lzy==2){
d[d[u].ls].h=max(d[u].h,d[d[u].rs].bl),d[d[u].rs].h=d[u].h;
}else{
d[d[u].ls].h=d[u].h,d[d[u].rs].h=max(d[u].h,d[d[u].ls].br);
}
d[u].lzy=0;
}
}
void build(int &u,int l,int r){
u=++tot;
if(l==r){
d[u].bl=w[l-1],d[u].br=w[l];
return;
}
int mid=(l+r)>>1;
build(d[u].ls,l,mid),build(d[u].rs,mid+1,r);
pushup(u);
}
int query_h(int u,int l,int r,int x){
if(l==r)return d[u].h;
int mid=(l+r)>>1;
pushdown(u);
if(x<=mid)return query_h(d[u].ls,l,mid,x);
else return query_h(d[u].rs,mid+1,r,x);
}
int query_l(int u,int l,int r,int x,int val){
if(d[u].bl<val)return -1;
if(l==r)return l;
int mid=(l+r)>>1;
pushdown(u);
if(x<=mid)return query_l(d[u].ls,l,mid,x,val);
int an=query_l(d[u].rs,mid+1,r,x,val);
return an==-1?query_l(d[u].ls,l,mid,x,val):an;
}
int query_r(int u,int l,int r,int x,int val){
if(d[u].br<val)return -1;
if(l==r)return l;
int mid=(l+r)>>1;
pushdown(u);
if(mid<x)return query_r(d[u].rs,mid+1,r,x,val);
int an=query_r(d[u].ls,l,mid,x,val);
return an==-1?query_r(d[u].rs,mid+1,r,x,val):an;
}
void pour_rb(int &u,int l,int r,int x,int y,int val){
u=abuild(u);
if(x<=l&&r<=y){
d[u].lzy=1,d[u].h=val;
return;
}
pushdown(u);
int mid=(l+r)>>1;
if(x<=mid)pour_rb(d[u].ls,l,mid,x,y,val);
if(y>mid)pour_rb(d[u].rs,mid+1,r,x,y,val);
// pushup(u,l,r);
}
void change_l(int &u,int l,int r,int x,int y,int &val){
u=abuild(u);
if(x<=l&&r<=y){
d[u].lzy=2,d[u].h=val;
val=max(val,d[u].bl);
return;
}
pushdown(u);
int mid=(l+r)>>1;
if(y>mid)change_l(d[u].rs,mid+1,r,x,y,val);//左边位置的水位取决于已查左板(将来右板)的高度;
if(x<=mid)change_l(d[u].ls,l,mid,x,y,val);
}
void change_r(int &u,int l,int r,int x,int y,int &val){
u=abuild(u);
if(x<=l&&r<=y){
d[u].lzy=3,d[u].h=val;
val=max(val,d[u].br);
return;
}
pushdown(u);
int mid=(l+r)>>1;
if(x<=mid)change_r(d[u].ls,l,mid,x,y,val);
if(y>mid)change_r(d[u].rs,mid+1,r,x,y,val);//右边位置的水位取决于已查右板(将来左板)的高度;
}
void change_b(int &u,int l,int r,int x,int val,int tp){
u=abuild(u);
if(l==r){
tp?(d[u].br=val):(d[u].bl=val);
return;
}
int mid=(l+r)>>1;
pushdown(u);
if(x<=mid)change_b(d[u].ls,l,mid,x,val,tp);
else change_b(d[u].rs,mid+1,r,x,val,tp);
pushup(u);
}
}T;
int main(){
gitgud();
n=read(),q=read();
w[0]=w[n]=inf;
for(int i=1;i<n;i++)w[i]=read();
T.build(rt[0],1,n);
for(int i=1;i<=q;i++){
int typ=read(),tim=read();
rt[i]=rt[tim];
if(typ==0){
int x=read(),val=read();
int hh=T.query_h(rt[i],1,n,x);
if(hh<val){
int xl=T.query_l(rt[i],1,n,x,val);
int xr=T.query_r(rt[i],1,n,x,val);
T.pour_rb(rt[i],1,n,xl,xr,val);
}
}else if(typ==1){
int x=read(),val=0;
int hh=T.query_h(rt[i],1,n,x);
int xl=T.query_l(rt[i],1,n,x,hh);
int xr=T.query_r(rt[i],1,n,x,hh);
val=0;
T.change_l(rt[i],1,n,xl,x,val);
val=0;
T.change_r(rt[i],1,n,x,xr,val);
}else if(typ==2){
int x=read(),val=read();
T.change_b(rt[i],1,n,x+1,val,0);
T.change_b(rt[i],1,n,x,val,1);
}else {
int x=read();
printf("%d\n",T.query_h(rt[tim],1,n,x));
}
}
return 0;
}
/*
4 9
1 3 2
0 0 4 2
3 1 1
0 2 4 3
3 3 1
0 4 4 4
3 5 1
2 6 1 4
1 7 4
3 8 1
*/
P2827 [NOIP2016 提高组] 蚯蚓
pts80:
首先考虑本题最大难点:蚯蚓生长规律。每秒除生成的蚯蚓外的所有蚯蚓长度增长 \(q\) 。
我们将增长的 \(q\) 的总和记为 \(qt\),将生成的两条蚯蚓各自长度减少 \(qt\) ,这样各条蚯蚓的长度差值不变。
将 \(qt\) 代入对蚯蚓长度的计算,用一个单调栈维护一下即可 。
pts100:
我们注意到,长蚯蚓分的两条小蚯蚓一定不比短蚯蚓分的两条小蚯蚓短,这是蚯蚓群自带的单调性。
将剪出来的蚯蚓放到两个队列中去,它们会自己形成单调队列。
将答案用单调栈维护一下就行了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define rgi register long long
#define FOR(i,a,b) for(int i=a;i<=b;i++)
#define ROF(i,a,b) for(int i=a;i>=b;i--)
const int M=2e5+7,inf=1e9+7,modd=998244353;
inline int read(){
int w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
inline void print(int n){
if(n<0){
putchar('-');
n=-n;
}
if(n>9)print(n/10);
putchar(n%10+'0');
}
int n,m,q,fz,fm,t,qt;
priority_queue<int>ans;
int qy[M],qy1[M*50],qy2[M*50];
int hd[4],tl[4];
void init(){
n=read(),m=read(),q=read(),fz=read(),fm=read(),t=read();
for(int i=1;i<=n;i++)qy[i]=read();
}
bool cmp(int aa,int bb){
return aa>bb;
}
void work(){
sort(qy+1,qy+n+1,cmp);
tl[1]=n,tl[2]=tl[3]=0,hd[1]=hd[2]=hd[3]=1;
for(rgi i=1;i<=m;i++){
int lg;
if(hd[1]<=tl[1]&&(hd[2]>tl[2]||qy1[hd[2]]<=qy[hd[1]])&&(hd[3]>tl[3]||qy2[hd[3]]<=qy[hd[1]]))lg=qy[hd[1]++]+qt;
else if(hd[2]<=tl[2]&&(hd[1]>tl[1]||qy[hd[1]]<=qy1[hd[2]])&&(hd[3]>tl[3]||qy2[hd[3]]<=qy1[hd[2]]))lg=qy1[hd[2]++]+qt;
else if(hd[3]<=tl[3]&&(hd[2]>tl[2]||qy1[hd[2]]<=qy2[hd[3]])&&(hd[1]>tl[1]||qy[hd[1]]<=qy2[hd[3]]))lg=qy2[hd[3]++]+qt;
if(i%t==0)print(lg),putchar(' ');
qt+=q;
int g=lg*fz/fm;
int q1=g-qt,q2=lg-g-qt;
// printf("%lld %lld %lld %lld\n",lg,g,q1,q2);
qy1[++tl[2]]=q1,qy2[++tl[3]]=q2;
// printf("result %lld\n",-hd[1]+tl[1]-hd[2]+tl[2]-hd[3]+tl[3]);
}
printf("\n");
for(int i=hd[1];i<=tl[1];i++)ans.push(qy[i]);
for(int i=hd[2];i<=tl[2];i++)ans.push(qy1[i]);
for(int i=hd[3];i<=tl[3];i++)ans.push(qy2[i]);
// printf("*****%d %d %d %d %d %d\n",hd[1],tl[1],hd[2],tl[2],hd[3],tl[3]);
int tim=0;
while(!ans.empty()){
tim++;
if(tim%t==0)print(ans.top()+qt),putchar(' ');
ans.pop();
}
}
signed main(){
// freopen("text.in","r",stdin);
// freopen("text.out","w",stdout);
init();
work();
return 0;
}
/*
3 7 1 1 3 1
3 3 2
*/
P2153 [SDOI2009] 晨跑
标准网络流题目。
将上午通信正解的优化建图减去,再稍微改一下,就做出来了。
code
同时,紫题100祭~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号