实验三

实验1

ans1：将分数转化为对应的等地；整型；字符型；

ans2：缺少break时，最终都是E

实验2

ans：累加上面的数据

ans2:相同，一个是累加，一个是递归

实验3

ans1：实现x的n次方的计算

ans2：:当n=0时，power(x)=0；n为奇，power(x)=x*power(x-1);n为偶，power(x)=power(x/2)*power(x/2)

实验4

#include <stdio.h>
int is_prime(int x);
#define N 100
int main() {
    int j;
    printf("100以内的孪生素数:\n");
    for (j = 2; j < N; ++j) {
        if (is_prime(j) ==1 && is_prime(j+2)==1) {
            printf("%d %d", j, j + 2);
            printf("\n");
        }
    }

}
int is_prime(int x) {
    int i;
    for (i = 2; i < x; ++i) {
        if (x % i == 0)
            return 0;
    }
    return 1;
}

实验5

 

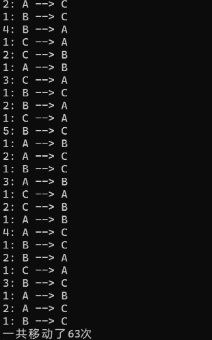
#include<stdio.h>
#include<stdlib.h>

int count = 0;

void hanoi(unsigned int n, char from, char temp, char to);
void moveplate(unsigned int n, char from, char to);

int main()
{
    unsigned int n;
    while (scanf_s("%u", &n) != EOF)
    {
        count = 0;
        hanoi(n, 'A', 'B', 'C');
        printf("一共移动的次数为：%d", count);
    }
    system("pause");
    return 0;
}

void hanoi(unsigned int n, char from, char temp, char to)
{
    if (n == 1)
        moveplate(n, from, to);
    else
    {
        hanoi(n - 1, from, to, temp);
        moveplate(n, from, to);
        hanoi(n - 1, temp, from, to);

    }
}
void moveplate(unsigned int n, char from, char to)
{
    printf("%u:%c-->%c\n", n, from, to);
    count++;
}

实验6

 

 

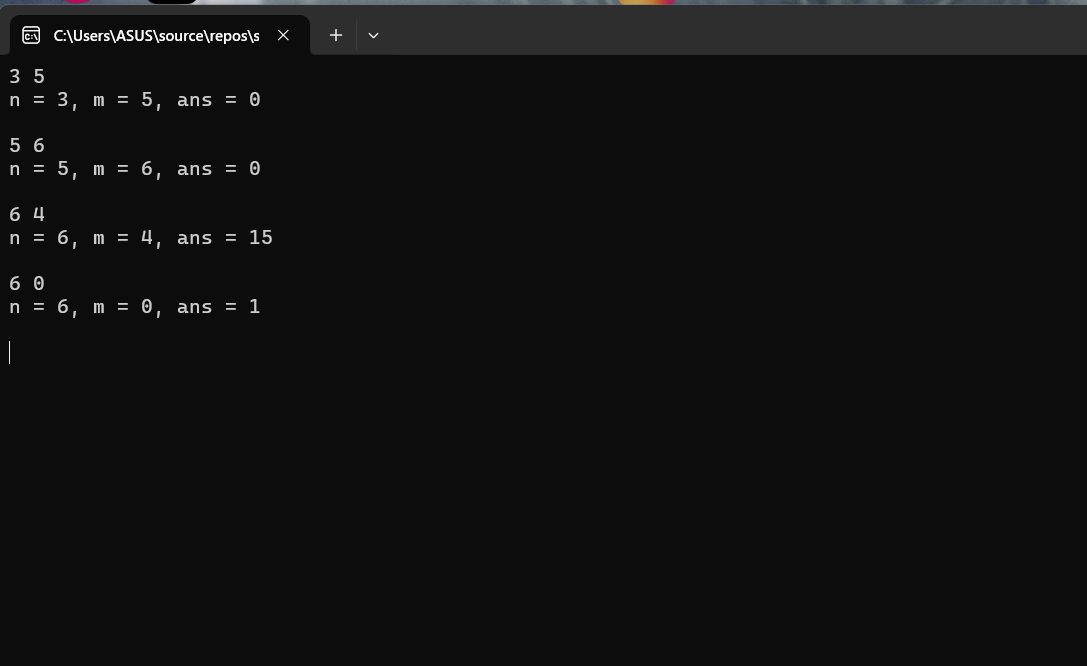
#include <stdio.h>
int func(int n, int m);   // 函数声明

int main() {
    int n, m;
    int ans;

    while (scanf_s("%d%d", &n, &m) != EOF) {
        ans = func(n, m);   // 函数调用
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }

    return 0;
}

// 函数定义
// 待补足。。。（分别用迭代和递归实现）
int func(int n, int m) {
    int sum ;
    if (m > n)
        sum = 0;
    else if (m == 0)
        sum = 1;
    else if (m == 1)
        sum = n-m+1;
    else {
        sum = func(n - 1, m - 1) * n / m;
    }
    return sum;
}

#include <stdio.h>
int func(int n, int m);   // 函数声明

int main() {
    int n, m;
    int ans;

    while (scanf_s("%d%d", &n, &m) != EOF) {
        ans = func(n, m);   // 函数调用
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }

    return 0;
}

// 函数定义
// 待补足。。。（分别用迭代和递归实现）
int func(int n, int m) {
    int ans;
    if (m > n)
        ans = 0;
    else if (m == 0)
        ans = 1;
    else if (m == 1)
        ans = n - m + 1;
    else
        ans = func(n - 1, m) + func(n - 1, m - 1);
    return ans;

}

实验7

#include <stdio.h>
// 函数声明
// 待补足....
int gcd(int a, int b, int c);
int gcd2(int a, int b);
int main() {
    int a, b, c;
    int ans;
    while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
        ans = gcd(a, b, c); // 函数调用
        printf("最大公约数: %d\n\n", ans);
    }
    return 0;
}
int gcd(int a, int b, int c) {
    return gcd2(gcd2(a, b), c);
}
int gcd2(int a, int b) {
    while (b != 0) {
        int t;
        t = b;
        b = a % b;
        a = t;
    }
    return a;
}

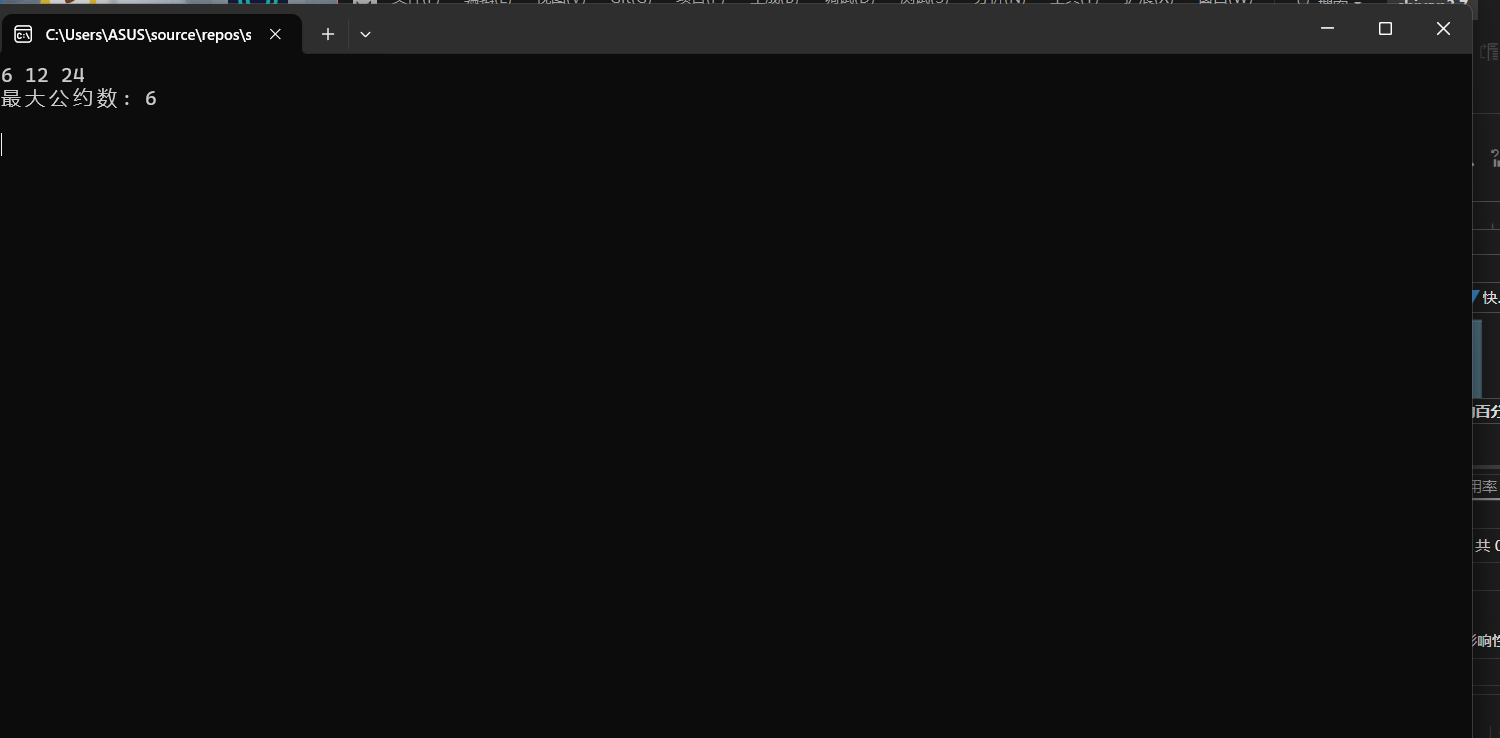
本次实验学习了函数的调用以及递归和累加的使用。