Arithmetic

图片均来自张进教授，仅为笔记用

目录

• 加减乘除
  • 加法
  • 减法
  • 乘法
  • 除法
• 浮点数
  • 浮点数表示
  • 精度的估算
  • 浮点数运算
    • 加法
    • 乘法
    • Rounding

加减乘除

加法

1bit adder

减法

减法的实现
\(a - b\) 就是 \(a\) 加上 \(b\) 的补码(2's complement)

Overflow的几种情况

1. 正数a + 正数b 得到 负数c
2. 负数a + 负数b 得到 正数c
3. 正数a - 负数b 得到 负数c
4. 负数a - 正数b 得到 正数c

乘法

最基础的乘法器
每次取multiplier的最后一位，如果是1就把multiplicand加到product上，然后multiplier右移一位，multiplicand左移一位，再进行循环

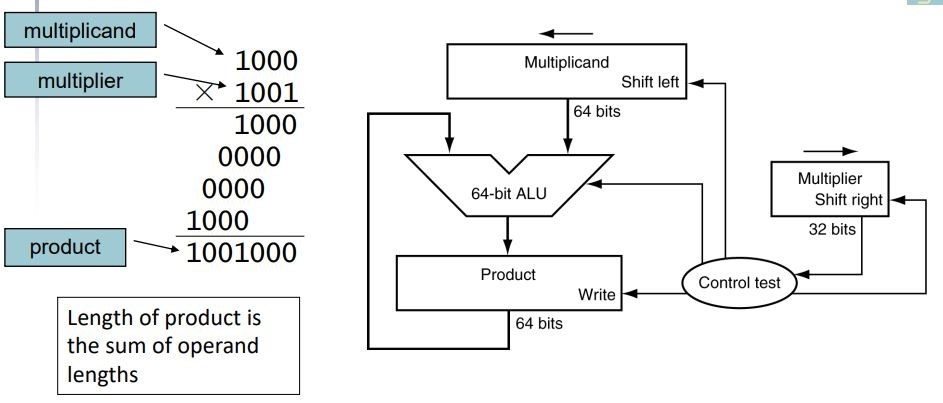
一个对空间优化过的乘法器：
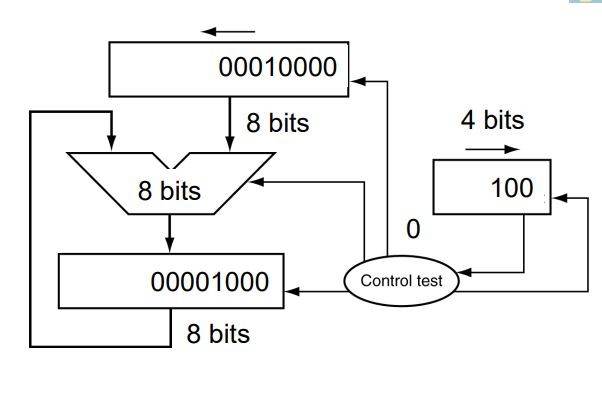
把multiplier和product放在一起，因为multipler的长度在减小，product的长度在增加，而他们长度加起来始终是64(32位乘法)
把multiplier放在该块内存的右边，product放左边，每次循环把该块内存整体右移一位
而且multiplicand不需要移位，在第n（从1开始）次循环时，是和product的高33-n位相加

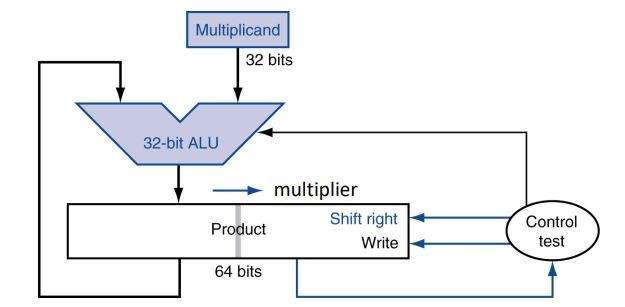
以上的乘法器是时序逻辑，需要时钟来控制每次循环，而以下的乘法器是组合逻辑，速度更快

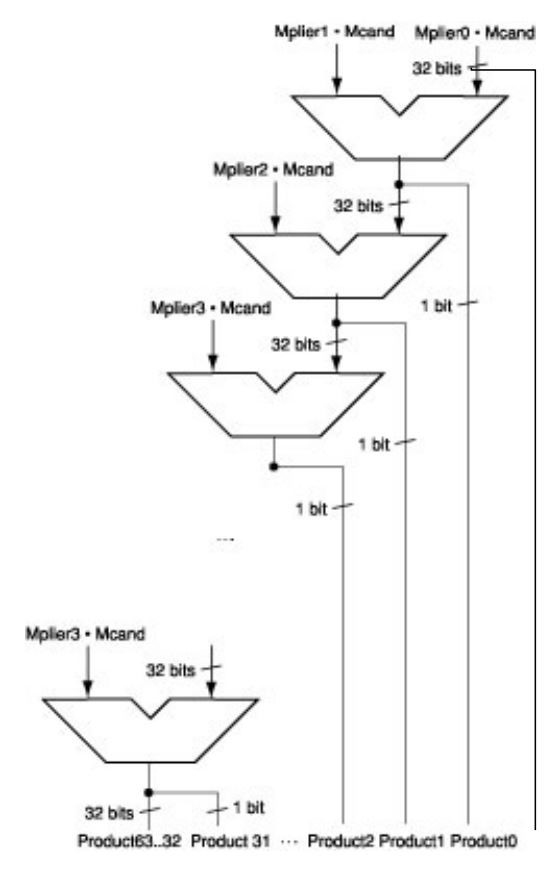
1. 该乘法器对于\(n\)位的multiplier，需要\(n-1\)个加法器，需要\(n-1\)次加法的时间才能完成整个乘法运算
   

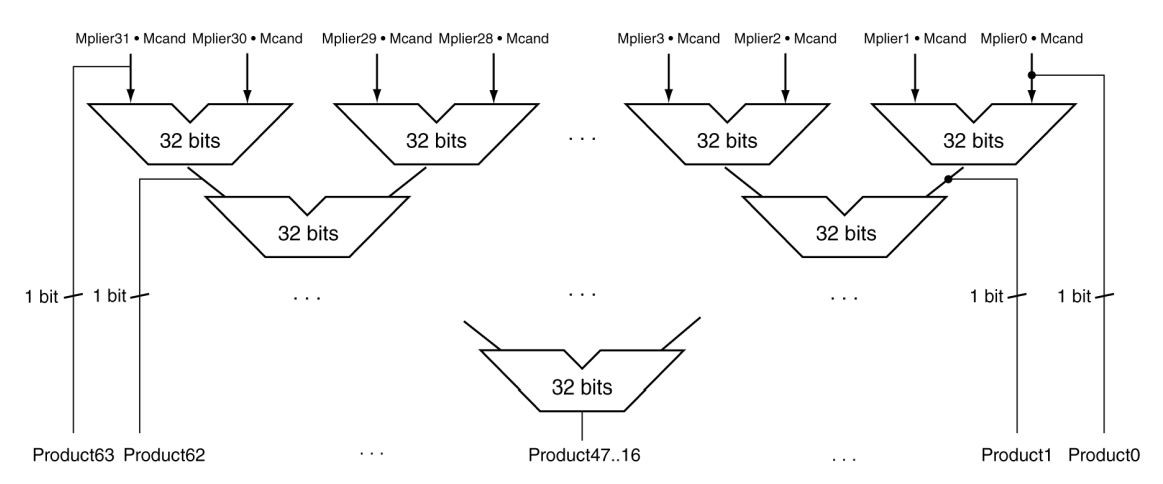
2. 该乘法器速度更快，需要\(n-1\)个加法器，需要\(log_2{n}\)次加法的时间完成整个乘法运算
   

除法

除法器(32位为例)的结构
Divisor, ALU, Remainder三块内存都有64位
把divisor放在内存的左半边，也就是从第33位（从1计数）开始放
remainder正常从最低位开始放
quotient一开始全为0

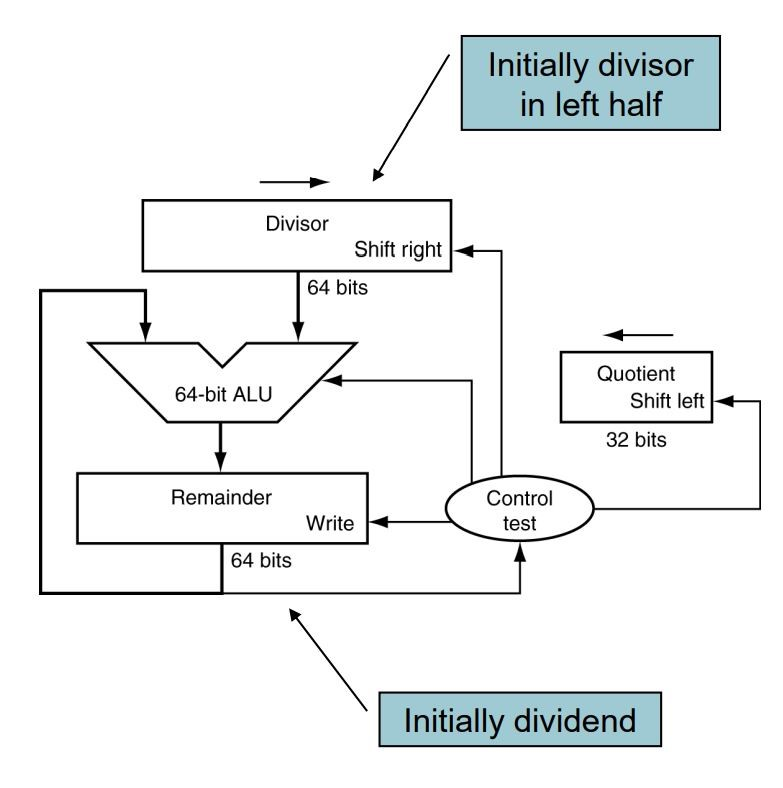
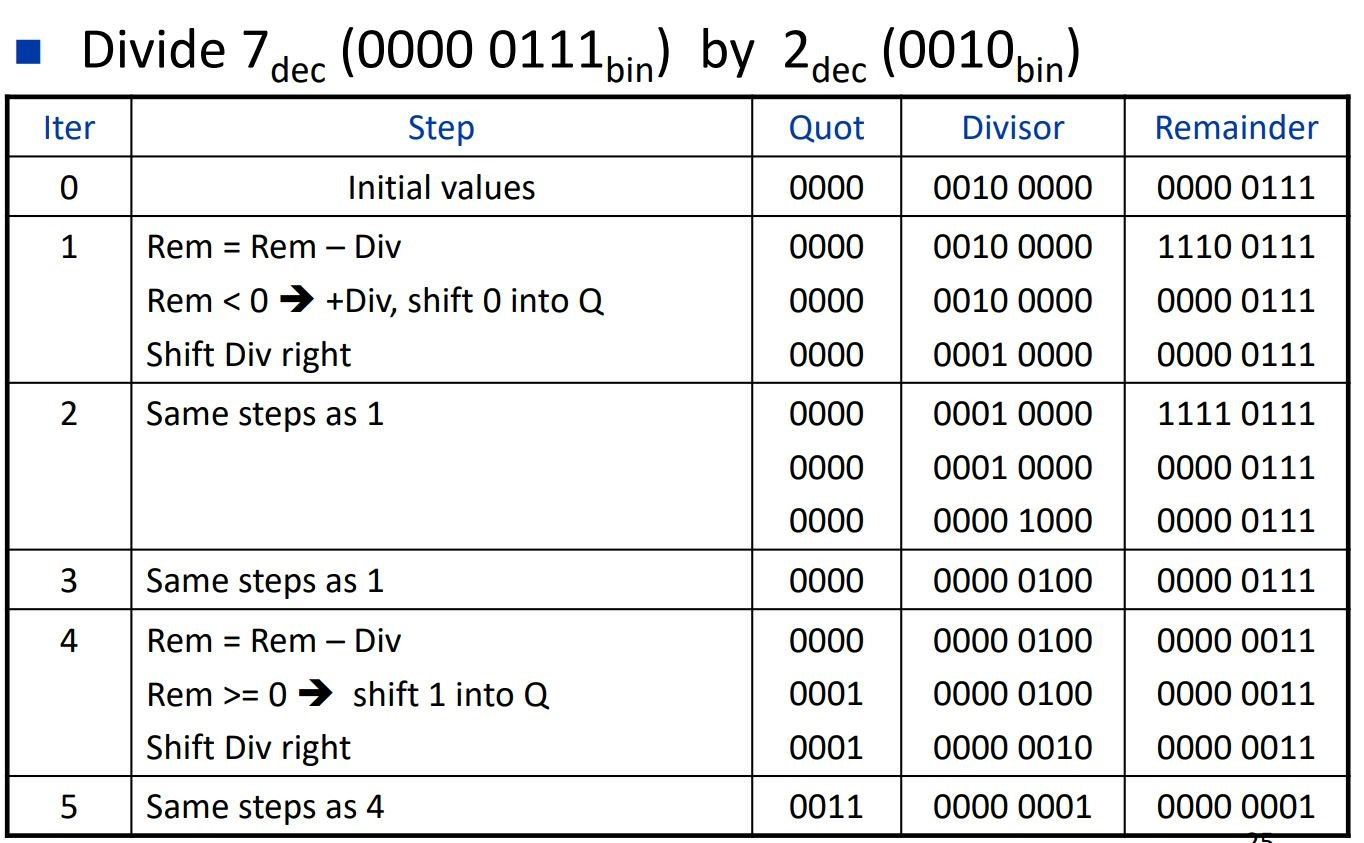
除法的步骤：

1. 每次用64位的remainder减去64位的divisor，存入remainder
2. 如果此时的remainder大于等于0，则quotient左移一位，然后+1；divisor右移一位
   否则，即此时的remainder小于0，给remainder加回减去的divisor；然后quotient左移一位，不加；divisor右移一位

然后回到第一步，这个循环需要进行33次，然后结束，得到结果的quotient和remainder
以下的图是一个简略过程，只进行了33次中最后几次作为示例，因为前面的几次都不会对示例中的remainder造成影响，实际在硬件中是严格执行33次的

优化的除法器
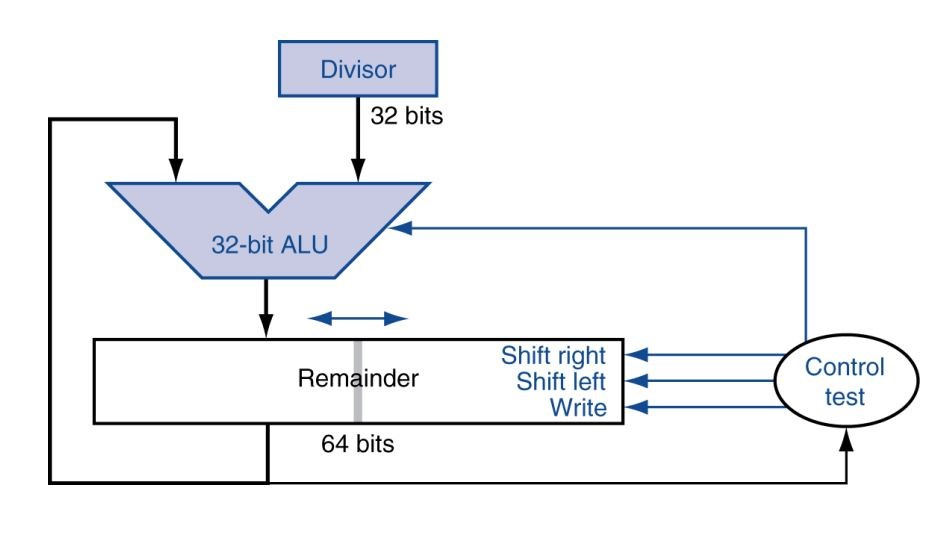
普通的除法器是保持remainder不动，divisor右移
优化结构是保持divisor不动，remainder左移增大。Divisor和ALU都只需要32位即可
remainder和quotient放在同一块内存中，一开始remainder从内存最低位开始放，quotient长度为0
每次都是用remainder的高32位减去divisor，然后remainder和quotient所在的内存左移，每次quotient的长度就会加1
也是重复进行33次后结束

浮点数

浮点数表示

以IEEE754为标准，浮点数的二进制记法
符号位+exponent+significand(也叫fraction, mantissa...)
这里的符号位用0表示正数，1表示负数
而exponent用移码的方式来表示，即原n位有符号exponent，加上\(2^{n-1}-1\)的bias
significand只用记小数点后面的部分，整数部分一定是1

我们把一些特殊的浮点数留出来，用来表示特别的数

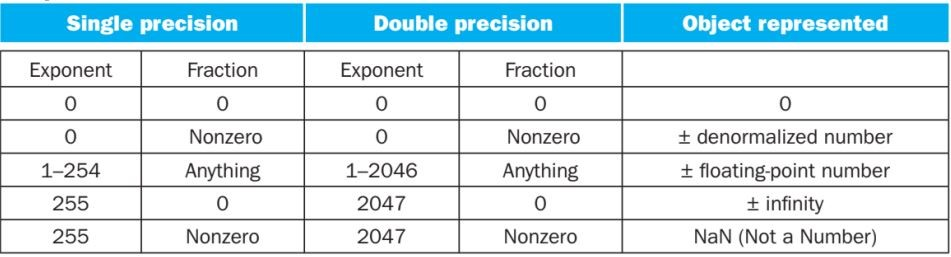
计算float和double的范围就很简单了，注意把特殊的位置留出来即可
下面是float的范围计算，double同理

normalized number的significand是用标准形式1.xxx
而当exponent是0时，代表denormalized number
denormalized number的siginificand是0.00…xxxx，隐藏的整数部分换成0，这样可以拓展浮点数的范围
而bias从\(2^{n-1}-1\)变成\(2^{n-1}-2\)
对于float，下限拓展了2^{-23，最小值变成了2}-149，但这样将会大大减慢浮点数的运算

精度的估算

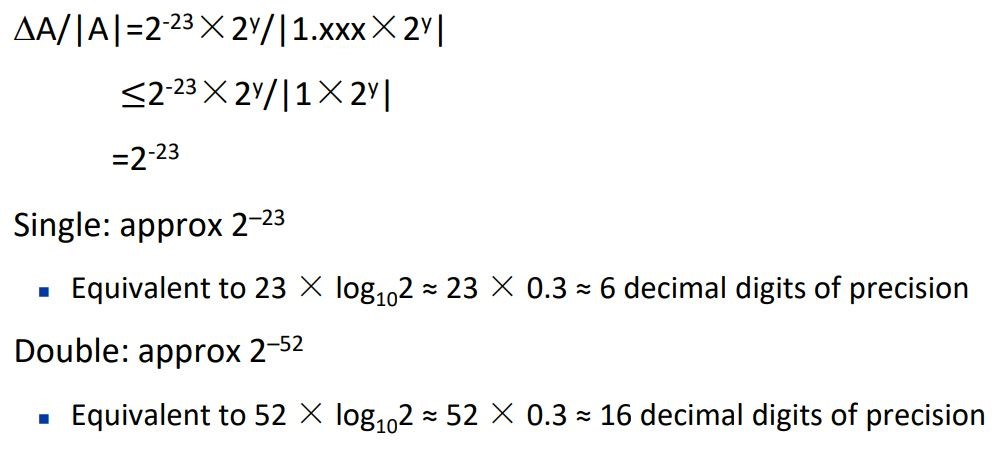
从二进制误差转到十进制精确位置的推导如下
\(2^{-x} = 10^{-y}\)
\(log_10{2^{-x}} = log_10{10^{-y}}\)
\(x \times log_{10}2 = y\)

浮点数运算

加法

浮点数的加法器如下

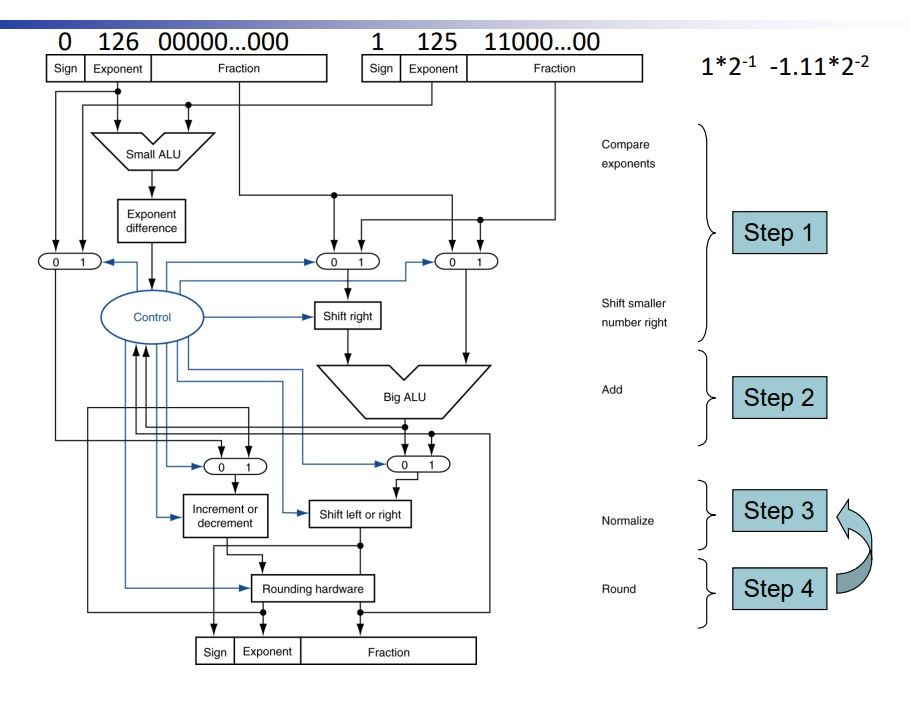
解析：

1. 图中第一层三个mux，最左边mux的判断哪个exponent较大，告知Control
   Control告知第二个和第三个哪个exponent较大，则对应的fraction不用动，另一个的fraction要右移
2. ALU把结果的fraction交给"shift left or shift right"，
   第一层第一个mux把较大的exponent交给"increment or decrement"
   要将fraction转换成标准形式，exponent也跟着做对应的操作
3. 把fraction和exponent交给rounding hardware，如果做了rounding后并非标准形式，则要通过第二层的mux来重新做"shift"，直到得到标准形式

乘法

乘法的运算步骤

Rounding

extra bits是在计算过程中间，在fraction部分后面补充的位数，用于减少精度丢失
一般用三个extra bits，分别命名为guard bit, round bit, sticky bit
假设用\(1.000 \times 2^5 - 1.001 \times 2^1\)
将exponent对齐后，变成\(1.000000 \times 2^5 - 0.0001001 \times 2^5\)
在1.000后面补的3个0就是extra bits
而0.0001001也应该rounding成小数点后六位来进行运算
rounding得到的结果是0.000101，第一个1是guard bit，紧接着下一位是round bit，再下一位是sticky bit，如果在原数中sticky bit及其之后的位数中存在大于等于一个1，则sticky bit就应该为1，否则为0

则使用extra bits的结果如下

最后要把结果rounding成三位小数，我们把结果中最低一位的1叫做unit in last place(ULP），在这个例子中ULP是0.001
如果extra bits部分大于0.5ULP，则向上取整；如果小于0.5ULP，则向下取整；如果恰好等于0.5ULP，则采用round to the nearest even，也就是使得rounding的结果最后一位是0