几何

目录

几何表示概述

几何图形可以通过隐式或者显式来表示
几何的隐式表示: 不知道点的实际位置，通过间接的方式来表达
几何的显式表示：知道所有点的确切位置

隐式表示

函数

函数表示的特点
1. 不直观，很难通过一个函数，直观得到三维图形的形状
2. 比较复杂的图形就很难用一个函数来表示
3. 通过带入函数，很容易判断一个点是否在图形上，图形内或图形外
4. 表示简单，存储简单，仅通过一个函数就能表达整个图形

Constructive solid geometry: CSG

通过几何图形的布尔运算，得到复杂的几何图形
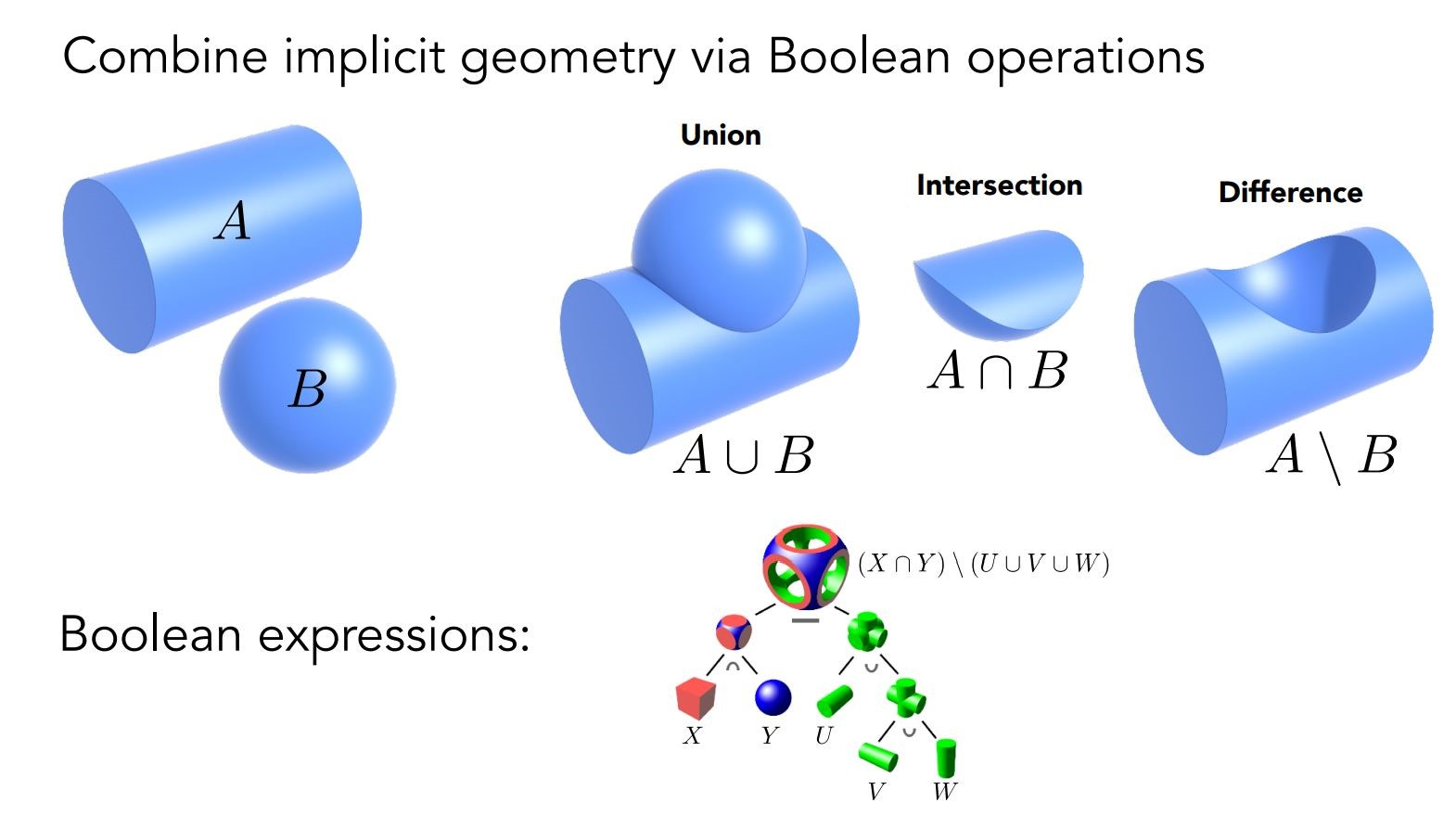
image

距离函数distance function

给出空间中任何一个点到特定物体表面/边界的最小距离
这里的距离可以有负数
距离函数适用于多个图形的融合

下述是一个利用SDF，即signed distance function做两个图形的融合操作
将A和B图中的阴影右边界当作物体边界，这样就得到两个SDF，边界左边为负，右边为正，将两个SDF融合起来，就会得到新的边界和新的SDF
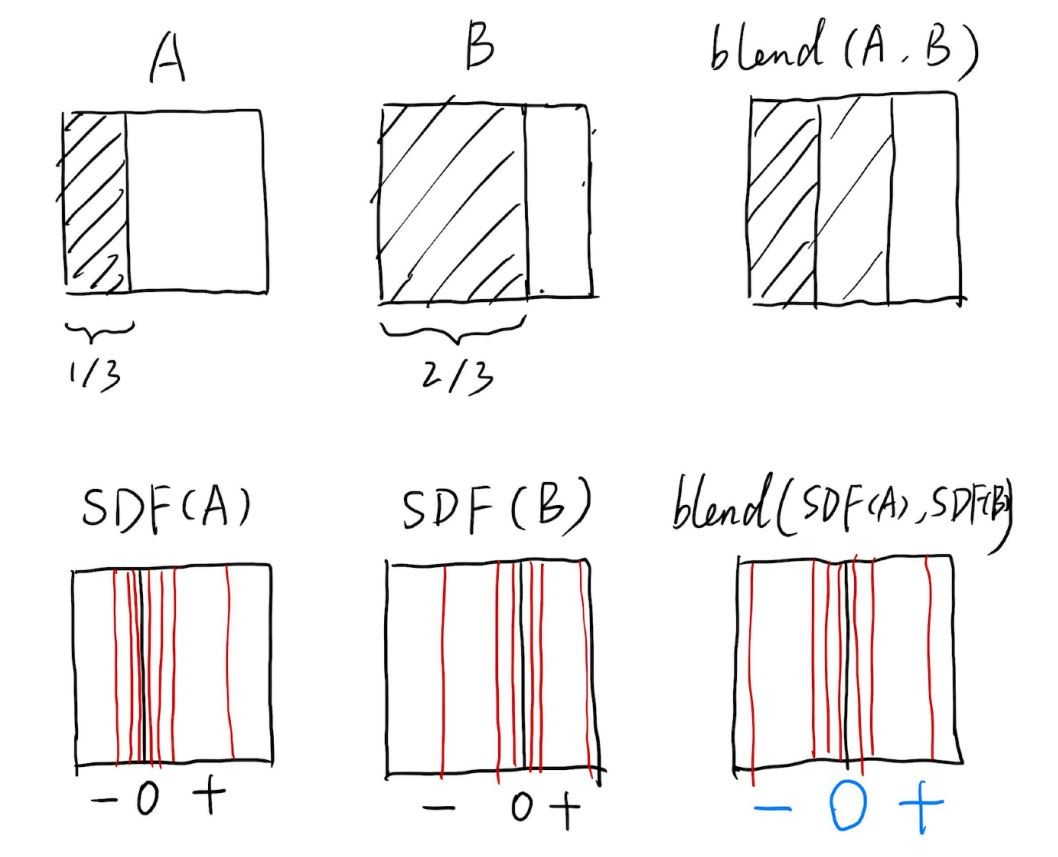
image

Level set method

和距离函数思想一致，但是是将SDF存在二维或是三维的格子中，再通过插值的方法，得到\(f(x)=0\)的一条线，即是边界
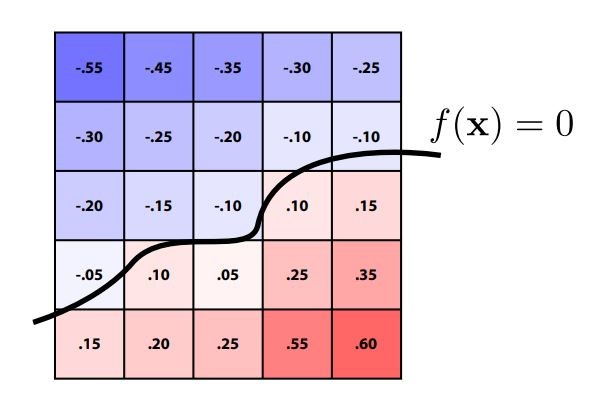
image

分形fractal

自己和自己的一部分有一样的形体
像这一种植物，植物有突起，突起中又有长得一样的突起
image

显式表示

显示表示概述

一种显式表示方法：全部的点都知道确切的位置

另一种显式表示方法：参数映射
给一个自变量空间加上一个函数，把所有的自变量点都走一遍，就得到因变量的三维图形
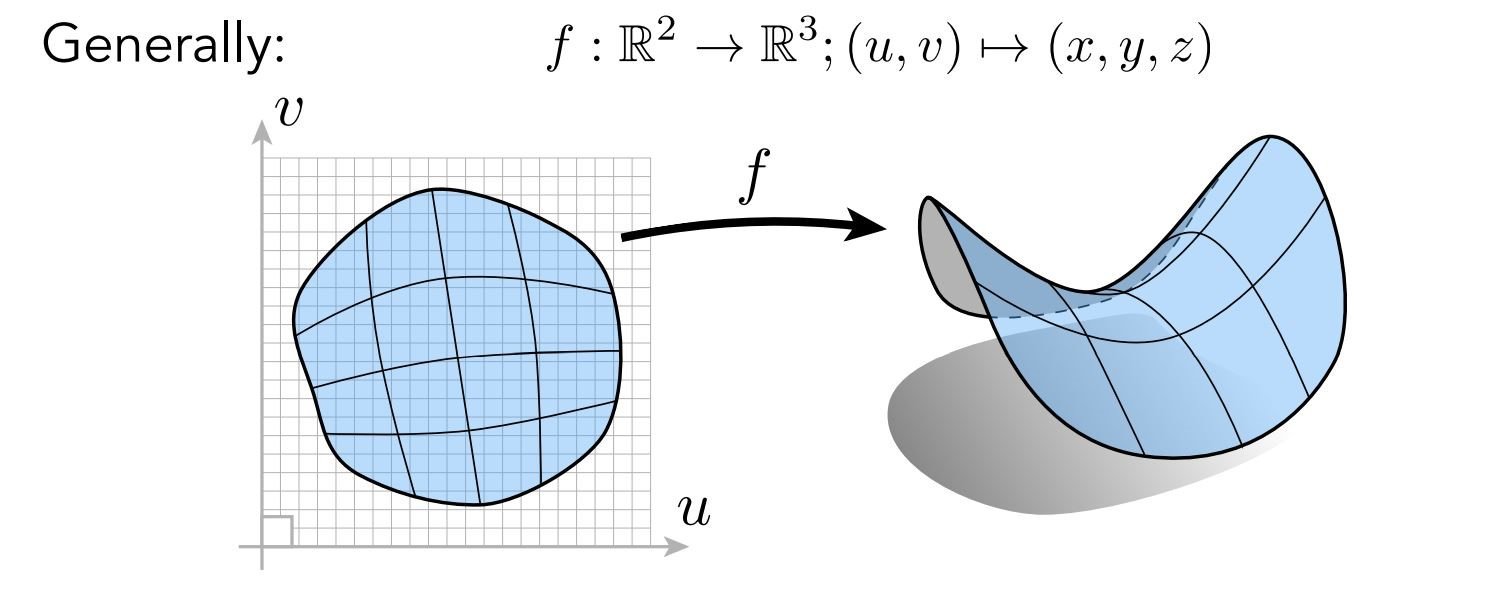
image

显式表示中，很难得知一个特定的点是在图形内，或是图形外

点云point cloud

物体的表面用离散的点来表示，当点的密度足够大，就近似形成了连续的表面
所以一个物体就是用一个点\((x, y, z)\)的列表来表示
需要大量的点数据
image

贝塞尔曲线Bezier Curves

贝塞尔曲线是通过一系列控制点，来得到特定的曲线

de Casteljau Algorithm
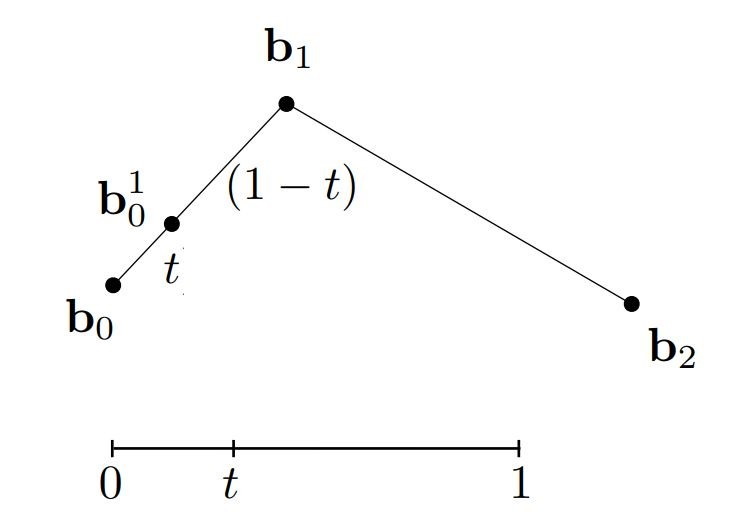
用控制点来画出贝塞尔曲线，我们要求曲线从\(b_0\)开始，到\(b_2\)结束，起始处切线为\(b_0b_1\)，结束处切线为\(b_1b_2\)
我们把曲线上的点用参数\(t\)，从一维到二维映射的方式来表示，使\(t \in [0,1]\)
想要找到t时刻的点，我们在每个线段上找出最靠左的t分位点，将每相邻两个线段上的两个点连接起来，得到新的直线，
进行递归，在得到的新的直线上重复找t分位点，并连接，直到得到唯一的一个t分位点
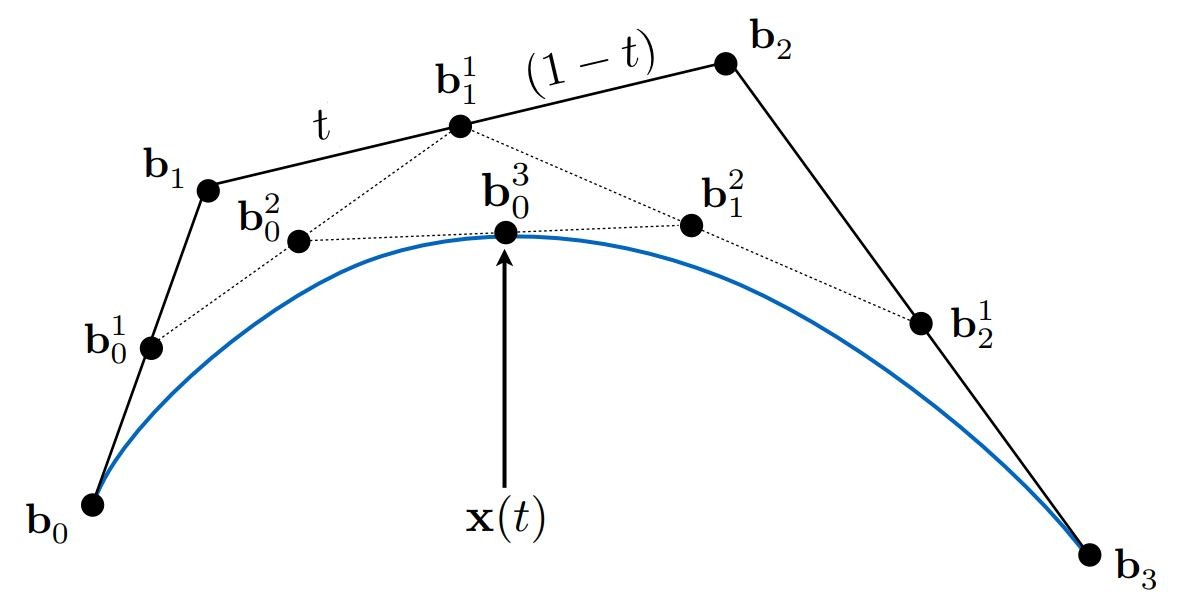
image

image

最终得到的\(x(t)\)可以用初始的控制点和\(t\)来表达
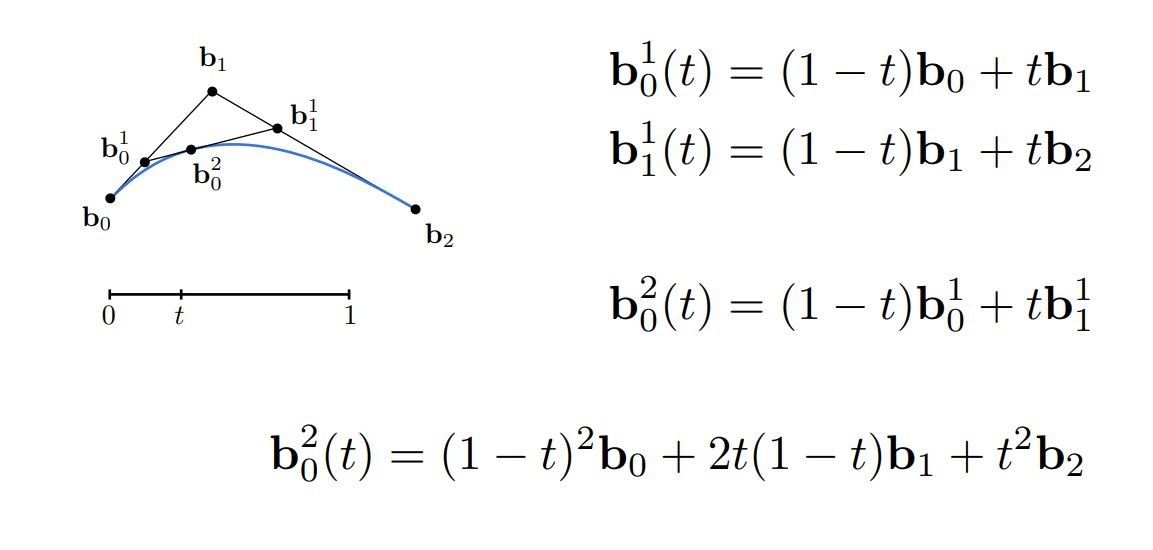
image

假设贝塞尔曲线为\(n\)阶，即有\(n\)条边，\(n+1\)个控制点，那么\(x(t)\)就可以用下述公式来表达
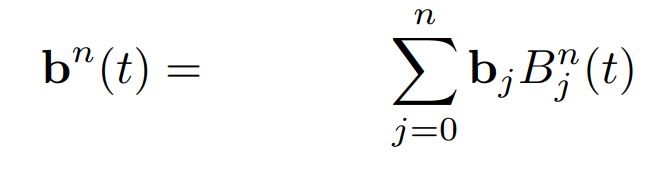
image

下述是Bernstein Polynomial
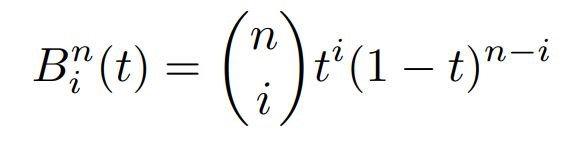
image

贝塞尔曲线的优秀性质：

  1. 仿射变换
    若要对贝塞尔曲线做仿射变换，可以对其控制点做仿射变换，再按照新的控制点画新的贝塞尔曲线，即可得到贝塞尔曲线的仿射变换
    但对其他的变换，比如投影变换就不适用

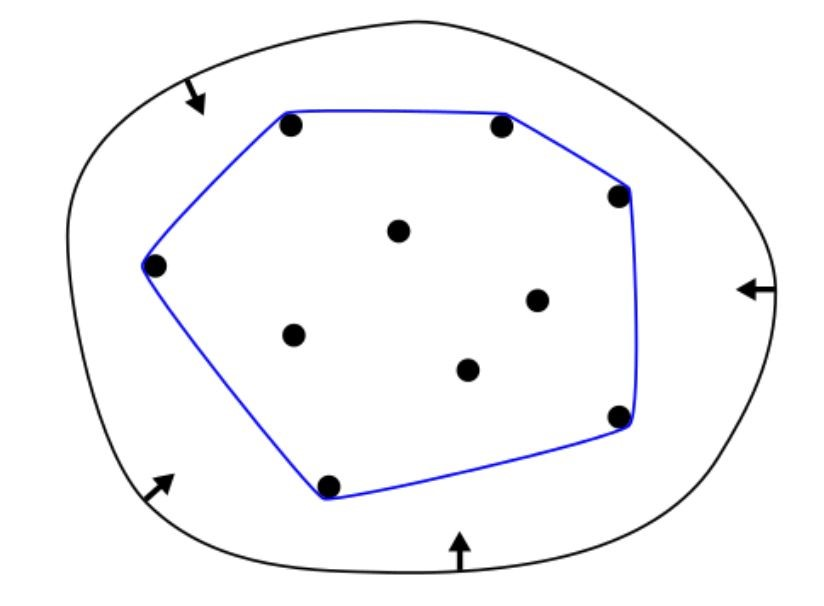
  2. 凸包
    二维平面内，凸包是能够包围一系列点的最小的凸多边形，可以想象成一条包围在几何体外围的橡皮圈，贝塞尔曲线一定在控制点的凸包内
    image

高阶的贝塞尔曲线
对于更高阶的贝塞尔曲线，我们可以用逐段地画贝塞尔曲线，再将每一段拼起来，而且我们倾向于用四个控制点得到的贝塞尔曲线来组成
因为太多控制点控制一个贝塞尔曲线，会很难对曲线进行控制，控制点的大幅度移动也只会小程度影响曲线
而且每一个控制点的移动，都会造成整条曲线的波动，无法进行分段细分控制
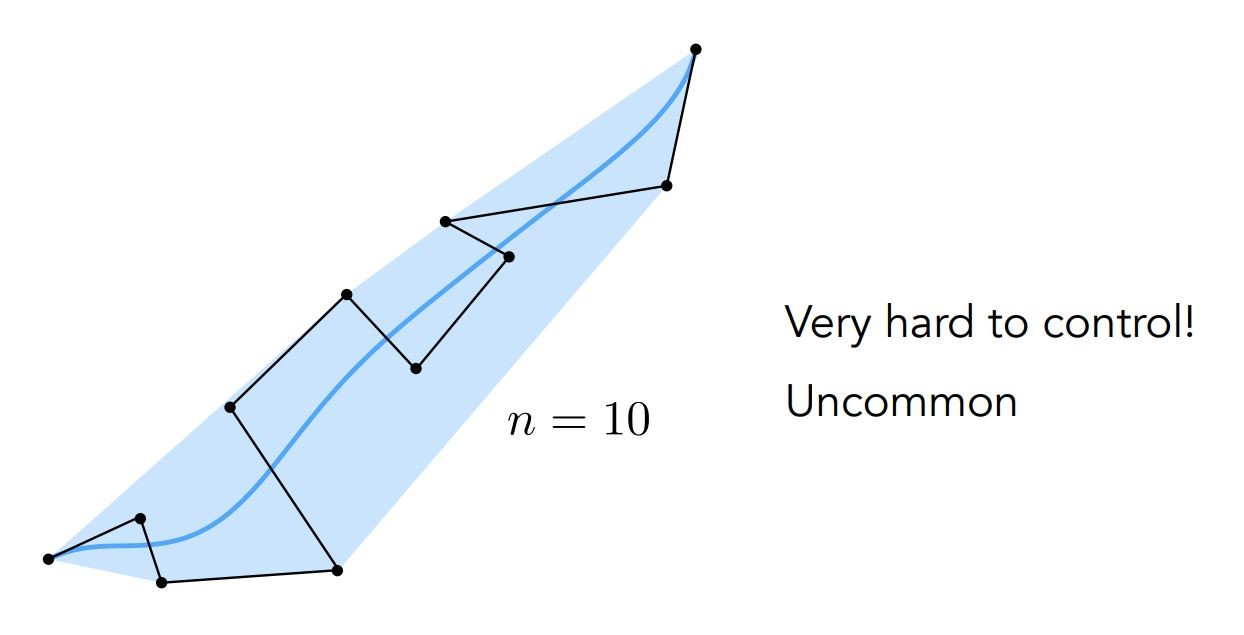
image

piecewise Bezier Curves则能更好地控制高阶贝塞尔曲线
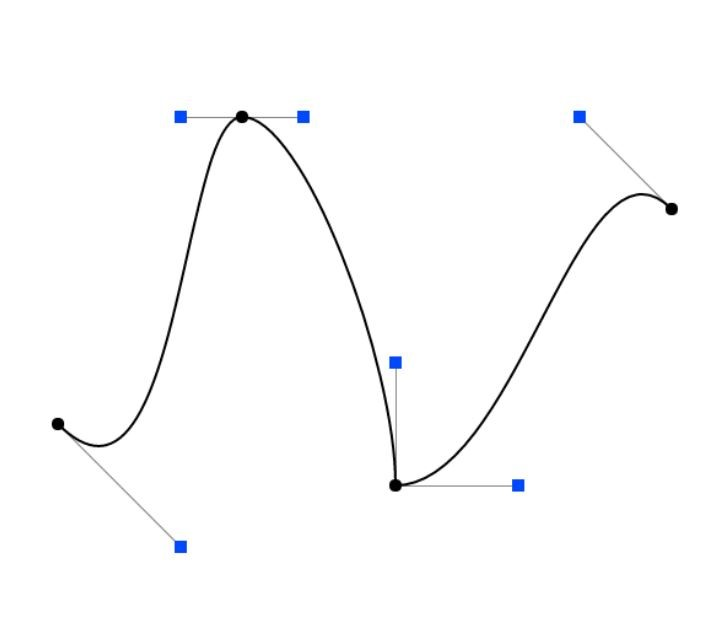
image

分段贝塞尔曲线的连续性

  1. \(C^0\)连续，两个分段相连接，即前一分段的终点，是后一分段的起始点
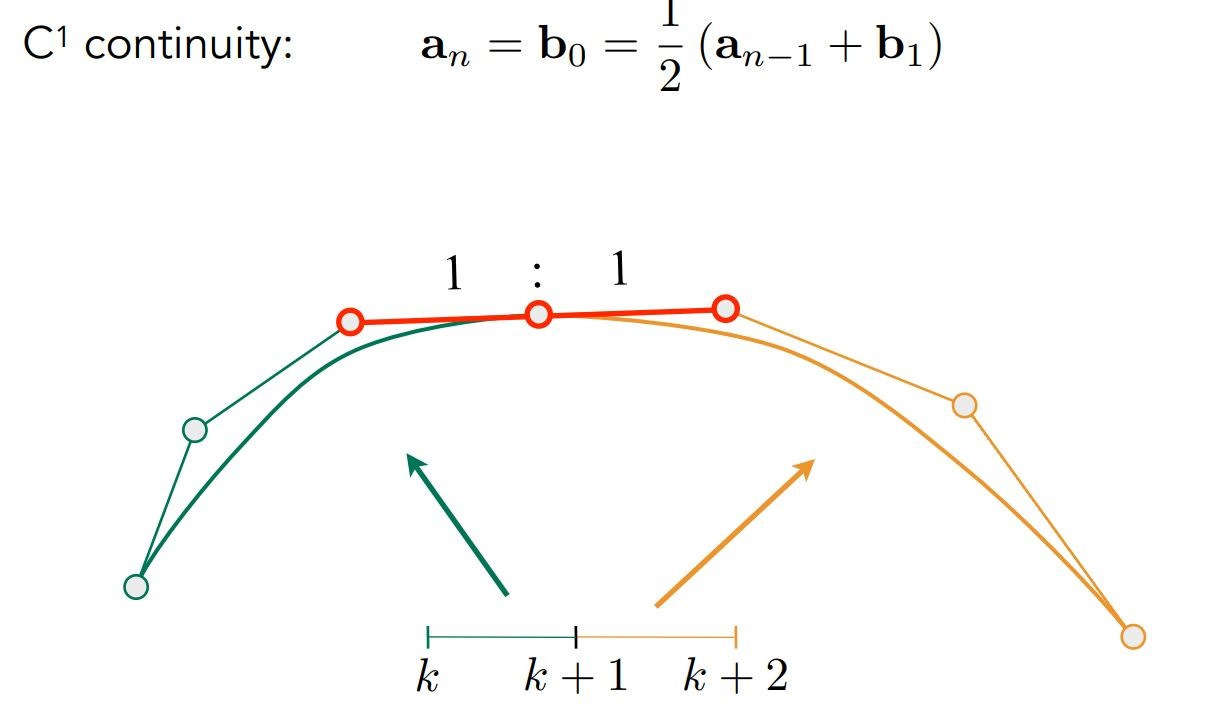
  2. \(C^1\)连续，即曲线光滑，我们用\(a_{n-1}\)来表示前一段的倒数第二个控制点，\(b_1\)来表示后一段的第二个控制点，如果两段相交的交点在\(a_{n-1}\)和\(b_1\)的中点，就可以保证曲线光滑
    image

贝塞尔曲面

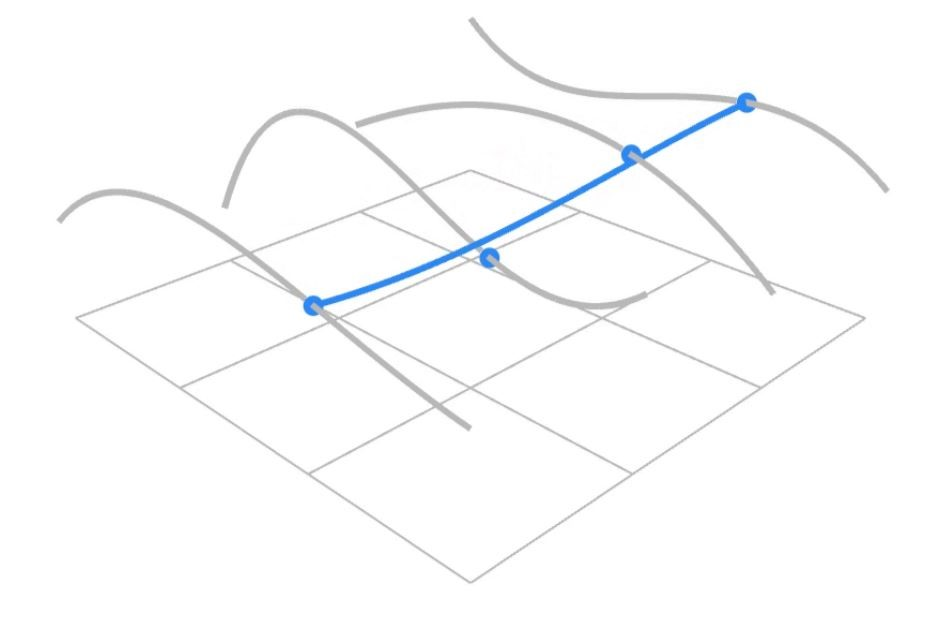
贝塞尔曲面，是做二维的的贝塞尔曲线，通过二维的参数\(u-v\)来映射到三维的曲面
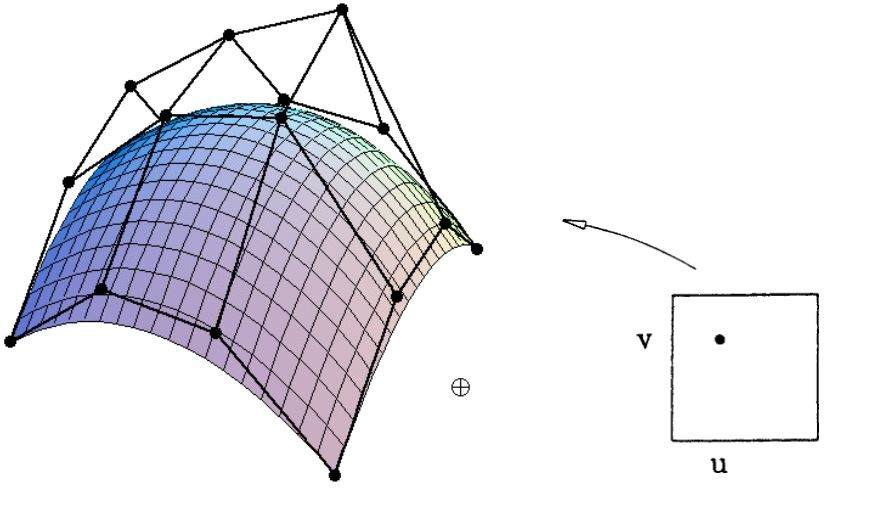
image

先是根据\(u\)得到\(u\)方向的多条贝塞尔曲线
在\(u = u_0\)时，我们取每一条贝塞尔曲线在\(u_0\)上的点，通过这些点来根据\(v\)来画另一条贝塞尔曲线，这一条曲线跟着\(u\)变化就会得到贝塞尔曲面
image

样条Spline

即一条可控的曲线，也是通过一些控制点来控制曲线

basis spline B样条
B样条满足贝塞尔曲线的所有性质
而且在移动控制点时，我们知道这个控制点影响的局部范围，不会影响整条曲线

多边形网格

用三角形、四边形来组成复杂的图形
是图形学中最广泛的显式表示，我们称之为多边形网格polygon mesh
image

存在几种操作
网格的细分：使得图形更光滑
网格的简化：减小存储量
网格的正则化：使得网格中不会出现过于特别的三角形，更趋向于正三角形
image

网格细分

Loop Subdivision

Loop division针对完全是三角形的网格进行细分
三角形的细分，不仅仅是将每个三角形拆成多个小三角形，更要对新的和旧的小三角形顶点的相对高度进行修改，才能使细分后的网格更加平滑
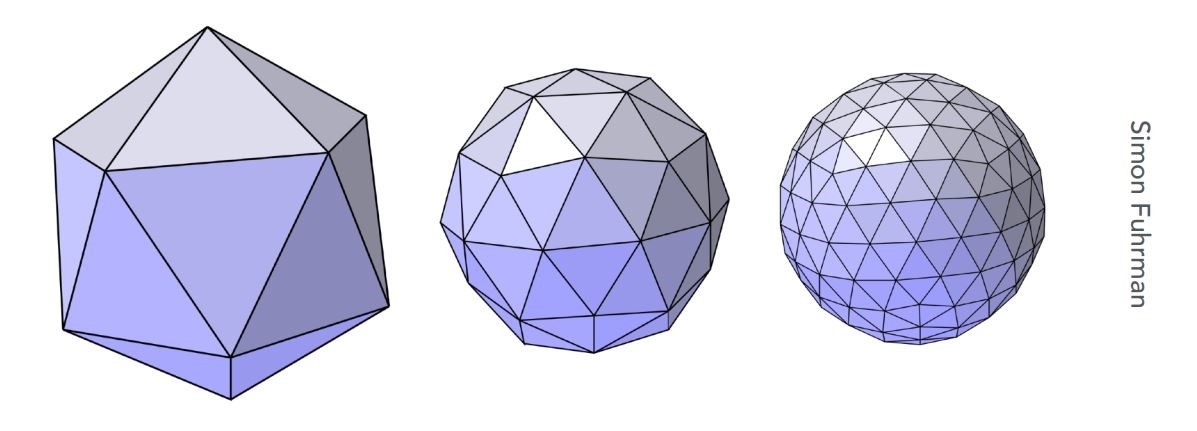
image

Loop division中，每个三角形会被细分成四个三角形，得到三个新顶点
对于得到的新顶点，新顶点的相对高度用下述方法计算
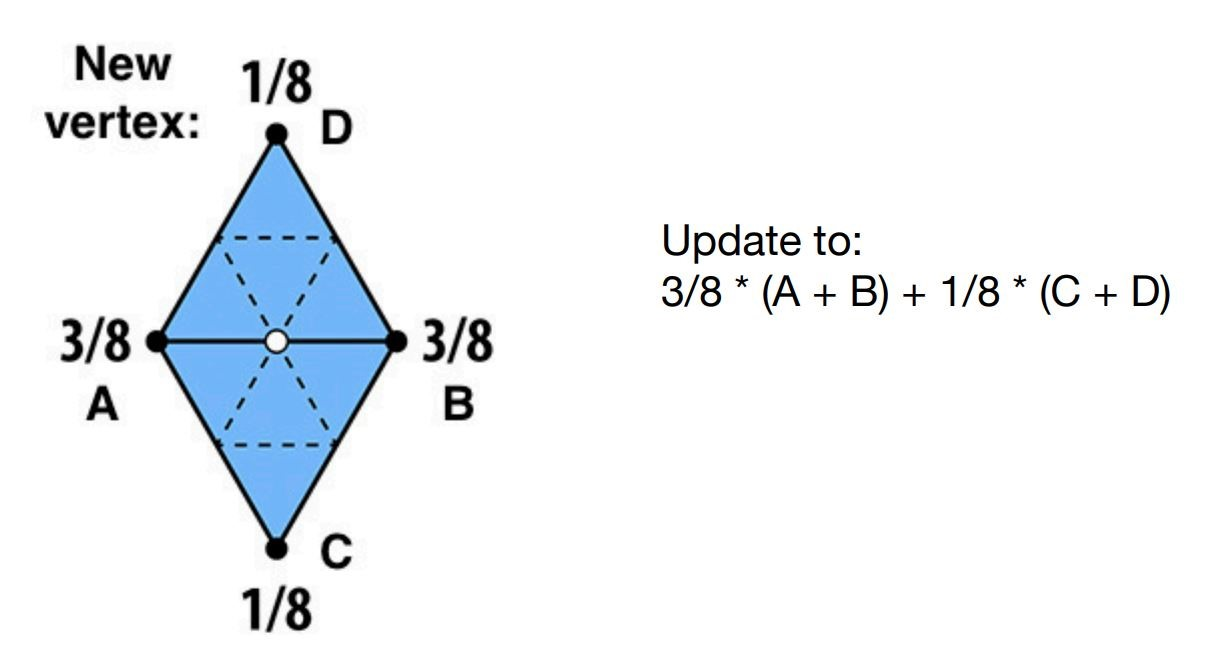
image

对于旧顶点的相对高度，用下述方法计算
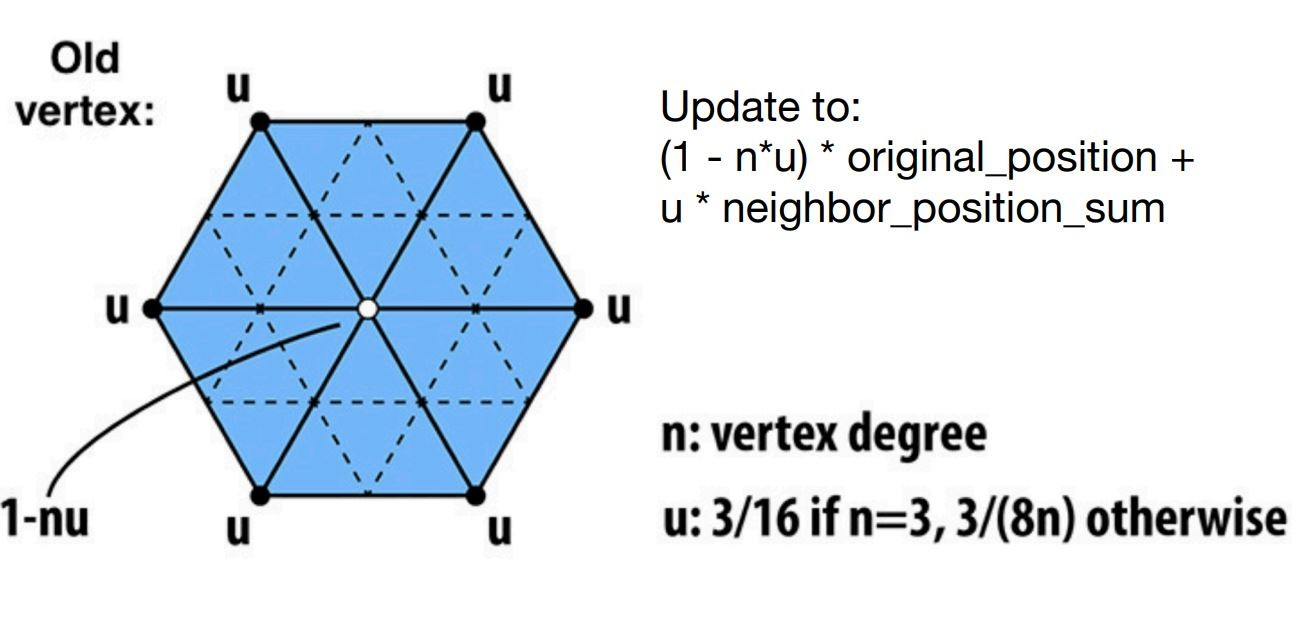
image

Catmull-Clark Subdivision

Catmull-Clark Subdivision可以细分所有类型的网格，不仅是三角形
我们定义非四边形的图形面叫做non-quad face
度不为4的顶点叫做extraordinary vertex
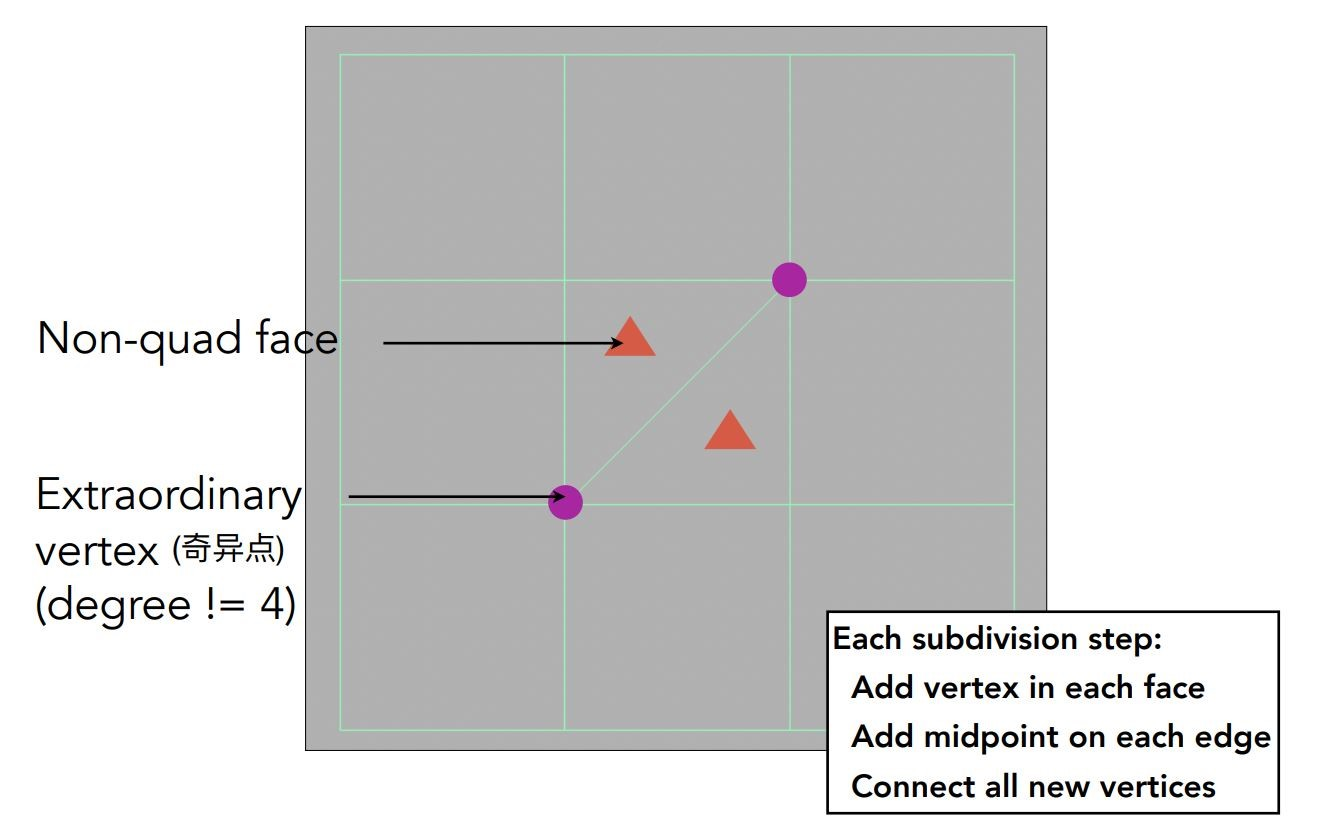
image

Carmull-Clark division的步骤

  1. 在每个面上加一个点
  2. 在每条边上加上一个中点
  3. 把面上的点与相邻边上的中点连接
    可以多次重复细分下去
    以上产生的新点就是新的顶点

在第一次division过后，若division前有\(n\)个non-quad face，那么division过后就会增加\(n\)个extraordinary vertex，且度都是3，并且所有non-quad face消失。在以后的division中，不会再有新的extraordinary vertex出现
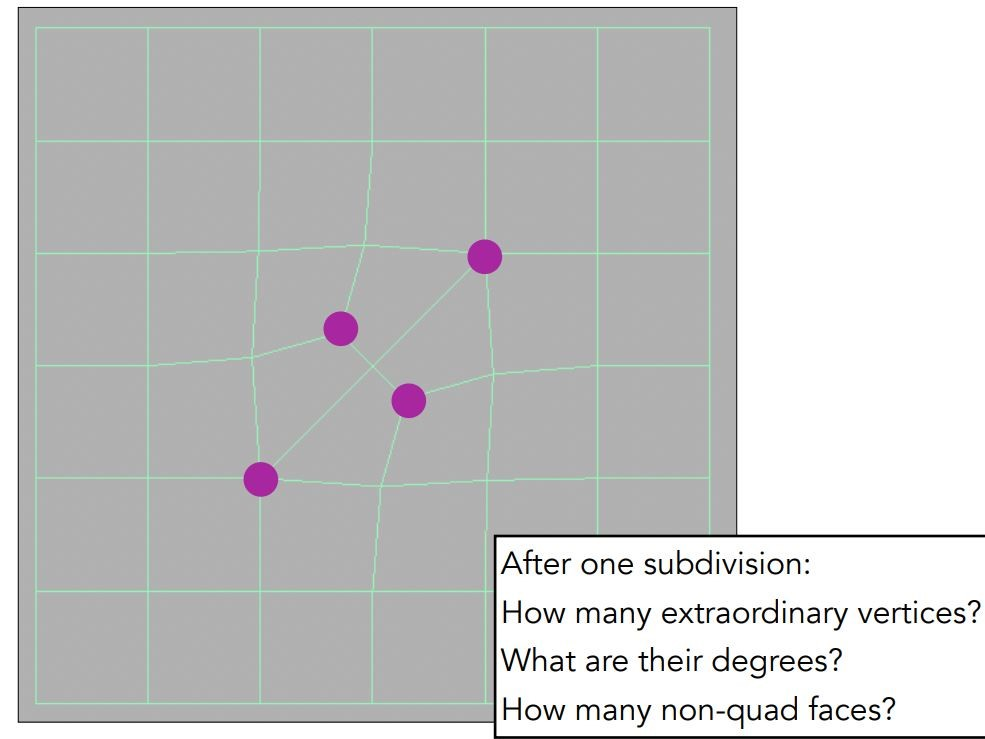
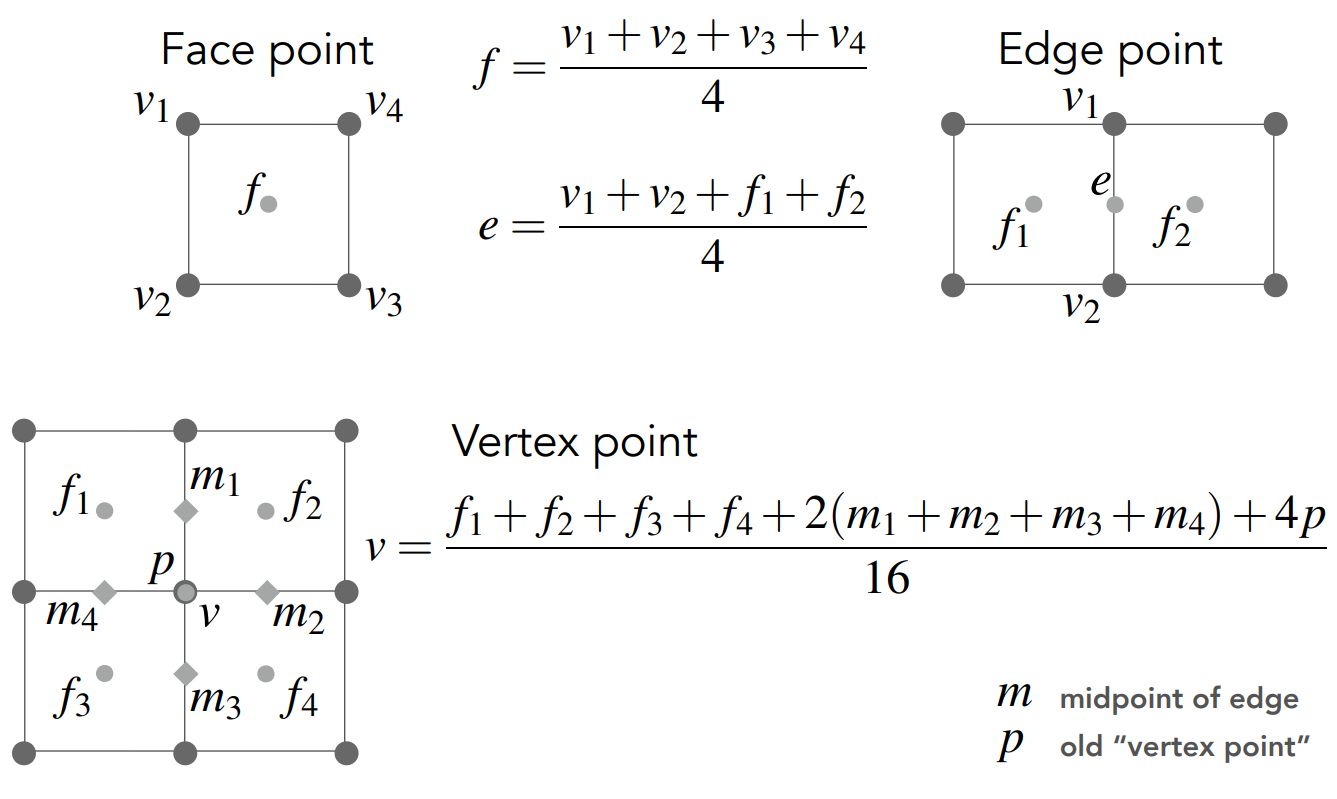
image

一次细分过后，我们要对所有顶点的高度以如下方式进行更新
image

网格的简化

当不需要这么细致的效果时，我们可以减少三角形的数量
image

我们用坍缩collapse的方式来减少三角形
我们针对特定的边来做坍缩，将边的两个顶点合在一起，得到一个新的顶点，原先两个顶点相连的其他边也会跟着移动
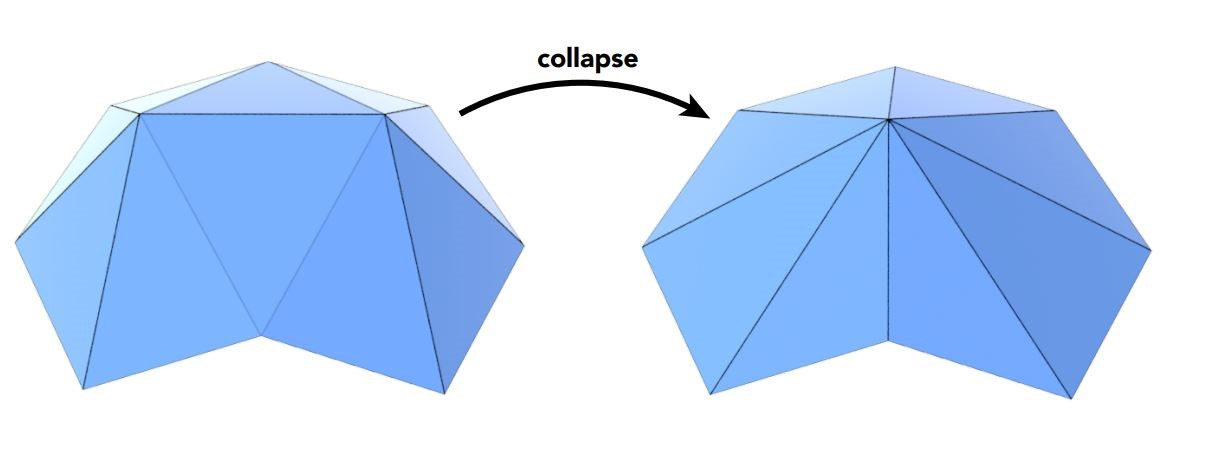
image

这个新的顶点我们通过优化后，摆在一个最优的位置，使得这个顶点的二次误差最小
二次误差指的是新顶点，到所有之前相连的面，按照变化前计算，距离平方之和
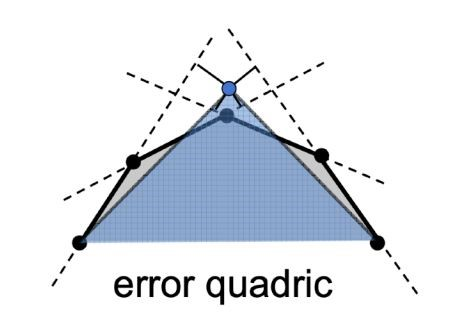
image

我们用一个贪心算法来对整个图形进行简化
先计算每个边，如果它坍缩会得到的二次误差
将每个边按照二次误差放入优先队列，每次对图形进行简化，就取出最小边进行坍缩
一条边坍缩后，会对其他边造成影响，二次误差也会改变，所以要对其他边进行更新

posted @ 2022-01-29 15:32  wcvanvan  阅读(745)  评论(0)    收藏  举报