k-d tree 学习笔记

什么是k-d tree

k-d tree 是一个把k维空间划分成一些区域的数据结构 方便对一些点进行查询和修改

例如一维的情况就是一棵二叉搜索树

二维的情况：

 

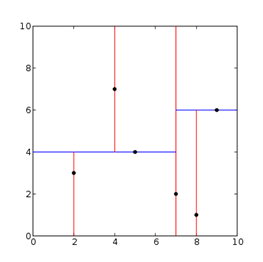
构造方法：

 

构建一棵k-d tree的方法和线段树类似

我们把k维空间里需要处理的点排成一行

每次我们找到当前处理区间的中间点，并用它将区间分为两块（在他一侧的和在他另一侧的）

然后递归处理两个子区间

 

较常用的是二维和三维的k-d tree

以二维的k-d tree为例，讲一下具体写法

首先我们对于每一个节点，维护一下几个量：

Left child, right child

Left-up corner, right-down corner 这用于记录区间对应的矩形的位置和大小，并且方便计算一个点到这个矩形的距离

Pivot-point 用于将这个区间分开的那个点

 

那么构建的过程中，每个量分别更新就好了

注意找中间点我们使用nth_element函数 作用就是找到一个区间里第k大的，并且将区间分成两块，比他小的和比他大的

 

 

可是究竟什么是中间点呢

 

一维的情况 中间点就是中位数

二维就有一些复杂了 理论上我们应该用某一维度将点集分开

那么选择哪一维度呢？ 最优的方法是选择所有维度中，方差最大的维度，也就是在这一维度上，点集对应的坐标最分散

但是我们如果这样枚举的话，白白增大了2~3的常数，所以在二位情况下，我们直接每次换一维度即可，也就是一横一竖一横一竖…… 这就能获得很好的复杂度了

三维还是老老实实判断方差吧……（好像还没有遇到三维的题目诶）

 

查询和修改

 

先讲修改

修改是很简单的，就像主席树那样，动态开点，然后每一次找到对应的儿子递归下去就好了

这个复杂度是严格$O(n \log n)$的

但是修改会影响到查询的复杂度，因为当你加了一堆点之后，你就不能保证你选择的分裂点依旧能将点集分成等大的两部分了

好像没有什么解决办法，只能硬着头皮上……

 

怎么在k-d tree上查询呢

首先我们要知道他能干什么

一般来说，我们用它来求最近点

就是输入一个点，在一个点集中快速找到和他最近的点

 

怎么做呢

我们用类似线段树的方法去找

因为每一个节点都对应着一个分裂点，就是分裂这个区间的点，我们称"计算这个点到被查询的点的距离并更新答案"为"用一个节点更新答案"

首先查询根 用根更新答案

然后判断这个点到根的两个子树对应的矩形哪个近

然后用近的那个子树去递归的搜索

注意一个问题：如果出现这种情况

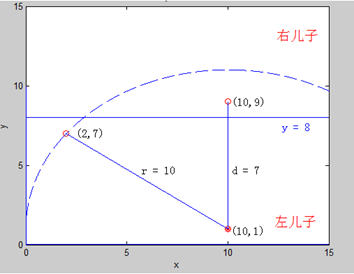
我们查询（10,1）发现他离左儿子对应的矩形更近，但是离他最近的点在右儿子里

所以当ans大于他到右儿子的距离的时候，我们再查询一下右儿子

 

于是复杂度就玄学了起来……

据说，k维的k-d tree的最坏复杂度是这样的

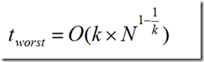
就是说二维的时候最坏$O(n \sqrt n)$

那么还是可以接受的嘛

 

实现

 

k-d tree在实现的时候有很多变种，因为事实上k-d tree就类似一个高维线段树，当然有很多应用，比如k远点对什么的

当然他也能被一些东西去替代，比如cdq分治什么的

 

那么贴上bzoj 2716的代码（请去https://darkbzoj.cf/problem/2716上提交）

就是一个支持加点，询问最近点的模板题

由于时限80s可以轻松过

 

  1 #include<stdio.h>  
  2 #include<cstring>  
  3 #include<cstdlib>  
  4 #include<algorithm>  
  5 #include<vector>  
  6 #include<map>  
  7 #include<set>  
  8 #include<cmath>  
  9 #include<iostream>  
 10 #include<queue>  
 11 #include<string>  
 12 using namespace std;  
 13 typedef long long ll;  
 14 typedef pair<int,int> pii;  
 15 typedef long double ld;  
 16 typedef unsigned long long ull;  
 17 typedef pair<long long,long long> pll;  
 18 #define fi first  
 19 #define se second  
 20 #define pb push_back  
 21 #define mp make_pair  
 22 #define rep(i,j,k)  for(register int i=(int)(j);i<=(int)(k);i++)  
 23 #define rrep(i,j,k) for(register int i=(int)(j);i>=(int)(k);i--)  
 24     
 25 ll read(){  
 26     ll x=0,f=1;char c=getchar();  
 27     while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}  
 28     while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}  
 29     return x*f;  
 30 }  
 31     
 32 const int maxn=1000100;  
 33 const int inf=1e9;  
 34 struct pnt{  
 35     int x,y;  
 36     pnt(){x=y=0;}  
 37     pnt(int a,int b){x=a;y=b;}  
 38 };  
 39 pnt ps[maxn];  
 40     
 41 int n,m;  
 42 int root,cnt;  
 43 bool dim;  
 44 struct Node{  
 45     pnt lu,rd,pp;  
 46     int l,r;  
 47 } tr[maxn];  
 48     
 49 void init(){  
 50     root=cnt=0;  
 51     tr[0].lu.x=inf;tr[0].lu.y=inf;  
 52     tr[0].rd.x=-inf;tr[0].rd.y=-inf;  
 53 }  
 54     
 55 bool cmp(pnt a,pnt b){  
 56     if(dim==0) return a.x<b.x || (a.x==b.x && a.y<b.y);  
 57     else return a.y<b.y || (a.y==b.y && a.x<b.x);  
 58 }  
 59     
 60 inline int getmin(int a,int b,int c){return min(a,min(b,c));}  
 61 inline int getmax(int a,int b,int c){return max(a,max(b,c));}  
 62     
 63 void upd(int x){  
 64     Node &L=tr[tr[x].l],&R=tr[tr[x].r];  
 65     tr[x].lu.x=getmin(tr[x].lu.x,L.lu.x,R.lu.x);  
 66     tr[x].lu.y=getmin(tr[x].lu.y,L.lu.y,R.lu.y);  
 67     tr[x].rd.x=getmax(tr[x].rd.x,L.rd.x,R.rd.x);  
 68     tr[x].rd.y=getmax(tr[x].rd.y,L.rd.y,R.rd.y);  
 69 }  
 70     
 71 int build(int l,int r,bool d=0){  
 72     if(l>=r) return 0;  
 73     int md=(l+r)>>1;  
 74     int ind=++cnt;  
 75     dim=d;  
 76     nth_element(ps+l,ps+md,ps+r,cmp);  
 77     tr[ind].pp=tr[ind].lu=tr[ind].rd=ps[md];  
 78     tr[ind].l=build(l,md,!d);  
 79     tr[ind].r=build(md+1,r,!d);  
 80     upd(ind);return ind;  
 81 }  
 82     
 83 void ins(int &x,pnt nw){  
 84     if(x==0){x=++cnt;tr[x].pp=tr[x].lu=tr[x].rd=nw;return;}  
 85     int d=cmp(nw,tr[x].pp);dim=!dim;  
 86     if(d==1) ins(tr[x].l,nw); else ins(tr[x].r,nw);  
 87     upd(x);  
 88 }  
 89     
 90 int dis(pnt a,pnt b){  
 91     return abs(a.x-b.x)+abs(a.y-b.y);  
 92 }  
 93 int dis(pnt p,int x){  
 94     int ret=0;  
 95     if(p.x<tr[x].lu.x) ret+=tr[x].lu.x-p.x;  
 96     else ret+=p.x-tr[x].rd.x;  
 97     if(p.y<tr[x].lu.y) ret+=tr[x].lu.y-p.y;  
 98     else ret+=p.y-tr[x].rd.y;  
 99     return ret;  
100 }  
101     
102 int ans;  
103 void ask(int x,pnt nw){  
104     if(x==0) return;  
105     ans=min(ans,dis(nw,tr[x].pp));  
106     int dc[2]={dis(nw,tr[x].l),dis(nw,tr[x].r)};  
107     if(dc[0]>dc[1]) ask(tr[x].r,nw); else ask(tr[x].l,nw);  
108     if(dc[0]>dc[1] && dc[0]<ans) ask(tr[x].l,nw);  
109     if(dc[1]>=dc[0] && dc[1]<ans) ask(tr[x].r,nw);  
110 }  
111     
112 int main(){  
113     init();  
114     n=read(),m=read();  
115     rep(i,0,n-1)  
116         ps[i].x=read(),ps[i].y=read();  
117     root=build(0,n);  
118     while(m--){  
119         int t=read(),x=read(),y=read();  
120         if(t==1){  
121             dim=0;  
122             ins(root,pnt(x,y));  
123         }  
124         else{  
125             ans=inf;  
126             ask(root,pnt(x,y));  
127             printf("%d\n",ans);  
128         }  
129     }  
130     return 0;  
131 }

 

下面还有一道一模一样的题 bzoj 2648

但是时限紧了许多，所以用指针版的k-d tree才能过去

具体请看https://blog.sengxian.com/algorithms/k-dimensional-tree

posted @ 2018-08-21 23:05  wawawa8  阅读(291)  评论(0)    收藏  举报