1、二叉树的学习,前中后序遍历的实现
概念部分
关于数的常用数据
-
节点,二叉树当中的每个点可称为一个节点
-
根节点,最顶部的节点就是根节点,一棵树,有且唯一有一个最顶部的根节点
-
父节点,该节点下如果还有节点的话,那么他自身就是一个父节点
-
子节点,同理,如果该节点的上级还有节点的话,那么他自身也是一个子节点
-
权:节点的值即为节点的权
-
叶子节点,没有子节点的节点就是叶子节点
-
路径:从根节点到该节点的路线就叫做路径
-
子树:这个概念比较模糊,类似于父节点下有子节点,并且该父节点的上方还有节点?
-
层:位于同级目录下的节点他就是一层
-
树的高度:最大层数即为树的高度
-
森林:多颗子树形成的森林--根节点下的多颗子树
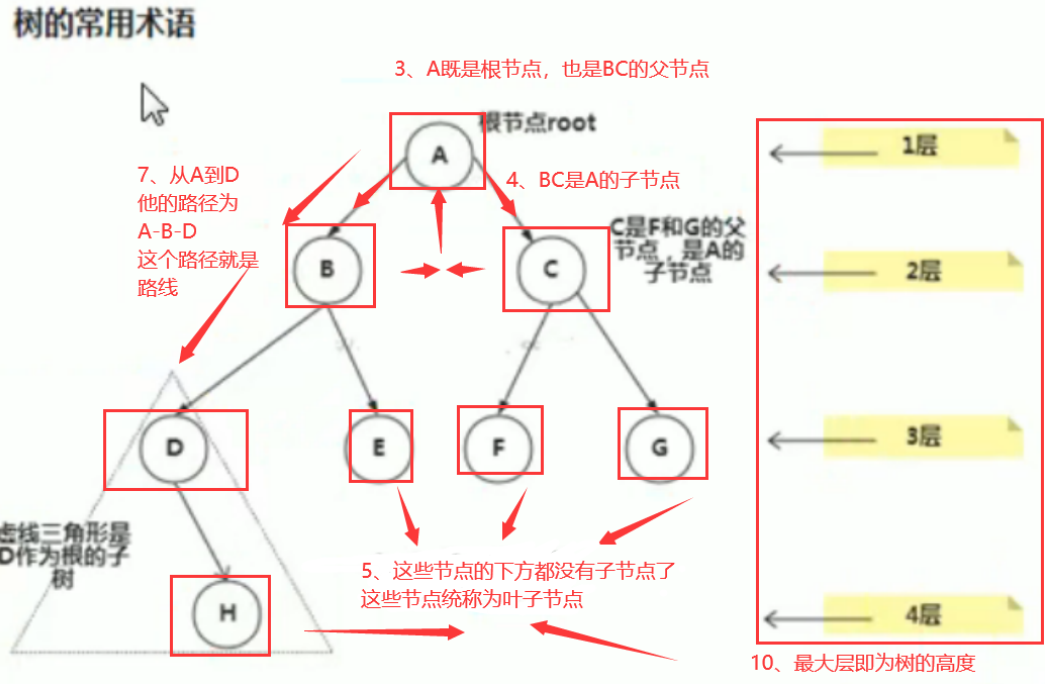
对于比较纠结的地方概念部分不用死钻,重点还是能够写出树这种结构,用树解决问题
1、二叉树
1,.1、二叉树的概念
-
树分为很多种,每个节点最多只能有两个子节点的树称之为二叉树
-
二叉树的子节点至多不能超过两个,所以它的子节点又被称为左节点和右节点
-
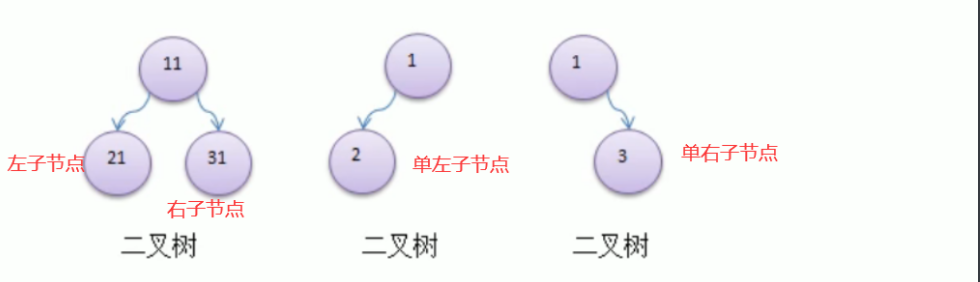
-
虽然后面两个二叉树只有一个子节点,但仍可以称作为二叉树,因为子节点至多存在两个嘛
-
-
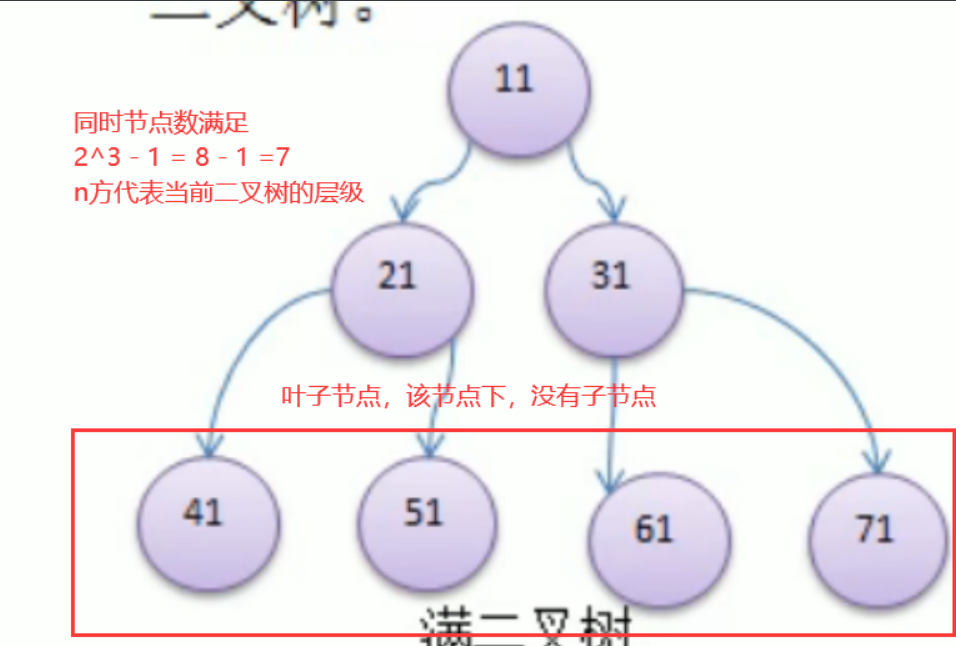
满二叉树:如果当前的二叉树,的,所有的,叶子节点都在最后一层,并且节点数的总数为:2^n - 1,(2的n方减一)
-
-
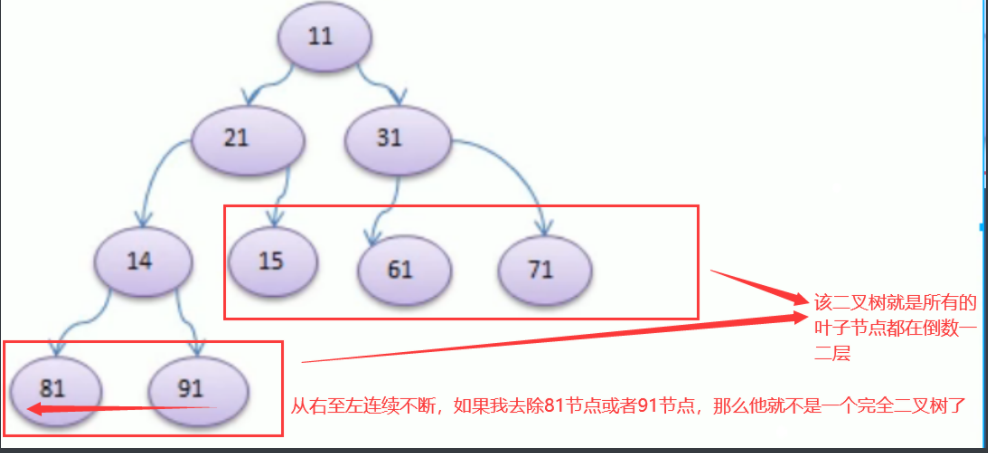
完全二叉树:如果该二叉树的所有叶子节点都在最后一层,或者是倒数第二层;
-
且,最后一层的叶子节点左边连续
-
倒数第二层的叶子节点右边连续
-
那么该树就可以称之为完全二叉树
-
-
什么是最后一层叶子节点左边连续?
-
-
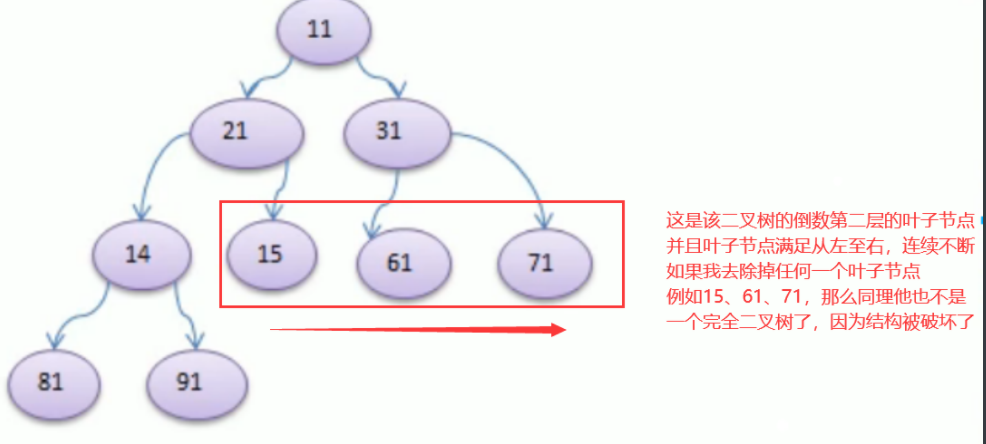
什么是倒数第二层的叶子节点右边连续?
-
1.2、二叉树的前中后序代码实现
1、节点类的设计
设计概念
-
二叉树是根据节点构成的,那么我们首先需要一个节点类Node对吧
-
其次就是对咱们Node节点类的设计
-
属性的设计
-
首先咱们需要知道每个节点的索引或者唯一性指标吧?这里我们就选择id作为唯一性指标
-
其次,既然是数据结构,数据结构的话内部需要存东西吧?那我们定义一个属性,叫做name吧(任意属性,T)
-
最重要的一点来了,二叉树,由节点构成,并且每个节点下的子节点至多不超过两个?什么意思?我们的节点需要子节点吗?需要,当然需要,子节点必须要有,并且左右都要有,你可以不对其进行值的赋予,但是他作为一个东西,必须有自身存在的意义,这是我的理解
-
那么我们就需要对其进行左右子节点的设计了
-
一个左节点,一个右节点,叫子树的话我觉得也可以吧?
-
-
-
代码设计
-
-
构造方法的设计
-
既然有这么一个节点Node,那当我在创建这个节点的时候,需要传递什么参数进去呢?
-
id作为一个节点的唯一性标识,这是我们需要的
-
而name的话作为该节点当中存储的数据也是我们需要的
-
左子节点和右子节点呢?需要吗?
-
不需要,因为一个节点本身确实是包含左右子节点还有其他属性构成的,但是,这个属性(子节点)只需要存在即可,知道有这么个东西,具体是否存在,看操作者的意愿,你想让他有子节点,那么他就有子节点,想让他没有,那他就没有,所以当我们进行有参构造的时候,不需要进行子节点的设计,但是会通过get和set方法去对子节点进行一个获取和赋值
-
-
-
代码设计
-
-
我们现在作为测试节点类的话,那肯定需要一个判断标识嘛,这个判断标识呢,我们就通过控制台打印的方式打印该节点的toString方法,当然,我们需要对其进行重写覆盖,不然打印出来的就是一串地址咯
-
同理,toString打印的时候需要打印什么属性?
-
id和name是必须的对吧?
-
左右子节点呢?不用吧?如果我这颗二叉树结构很复杂,那么我打印一个节点那不是要把屏幕撑爆?内容会相当的冗杂,所以我们这里就打印唯一性标识id和节点当中存储的数据内容name即可,自己该干嘛干嘛,别老想着一只公鸡要下蛋,不是你的活你非要干~
-
-
代码实现
-
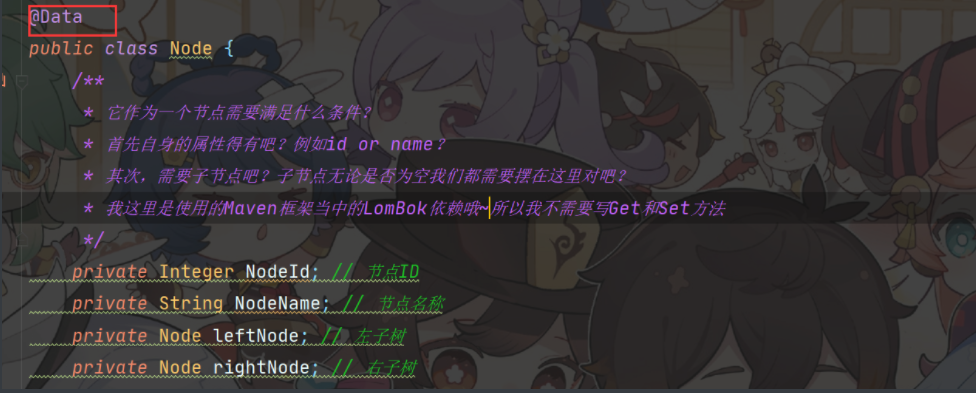
2、节点类的整体代码实现
/**
* 这是我们的节点类
*/
@Data
public class Node {
/**
* 它作为一个节点需要满足什么条件?
* 首先自身的属性得有吧?例如id or name?
* 其次,需要子节点吧?子节点无论是否为空我们都需要摆在这里对吧?
* 我这里是使用的Maven框架当中的LomBok依赖哦~所以我不需要写Get和Set方法
*/
private Integer NodeId; // 节点ID
private String NodeName; // 节点名称
private Node leftNode; // 左子树
private Node rightNode; // 右子树
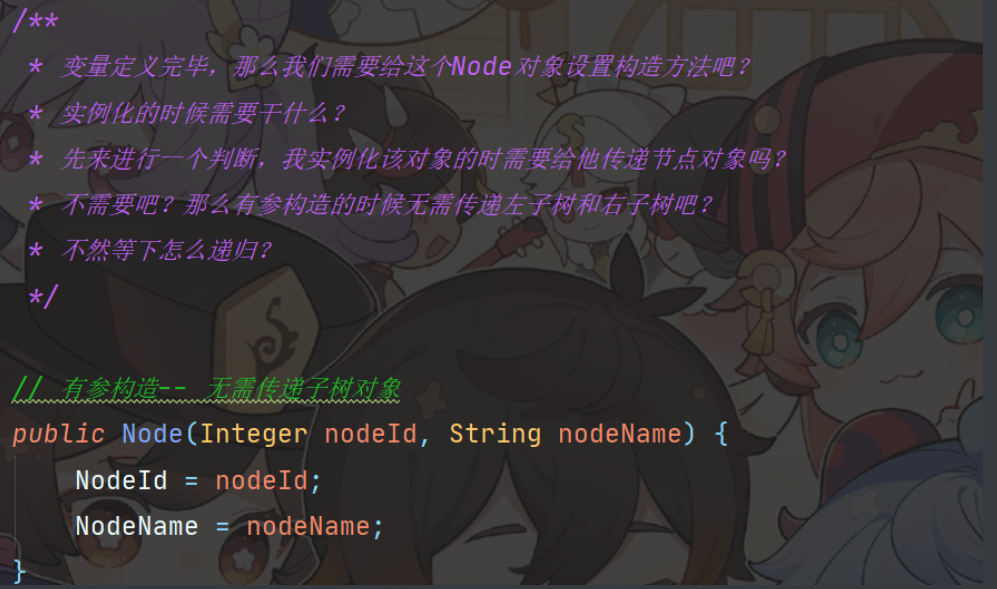
/**
* 变量定义完毕,那么我们需要给这个Node对象设置构造方法吧?
* 实例化的时候需要干什么?
* 先来进行一个判断,我实例化该对象的时需要给他传递节点对象吗?
* 不需要吧?那么有参构造的时候无需传递左子树和右子树吧?
* 不然等下怎么递归?
*/
// 有参构造-- 无需传递子树对象
public Node(Integer nodeId, String nodeName) {
NodeId = nodeId;
NodeName = nodeName;
}
/**
* 我定义的变量都是私有变量,那么我都需要给他们设置get和set吧?
* 有点麻烦了,那我引入一个Lombok简化我的开发吧,至少简化我get和set的开发吧?
* 没有使用Lombok的话就老老实实把get和set方法写上去哦
*/
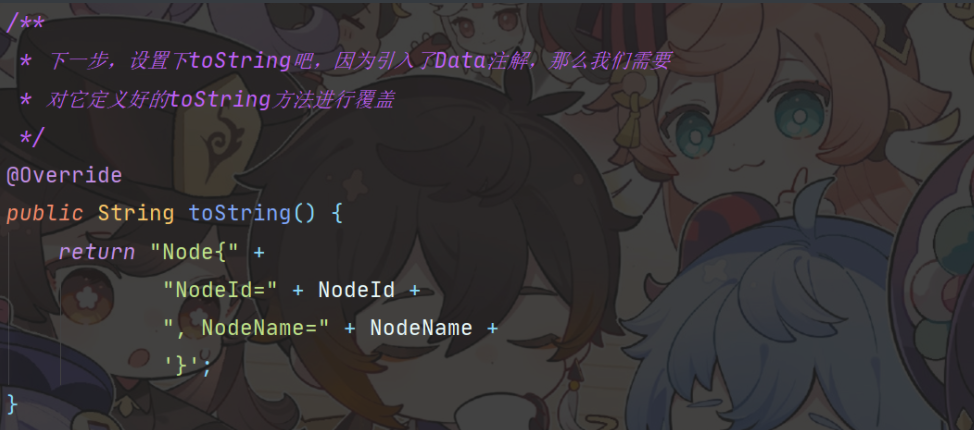
/**
* 下一步,设置下toString吧,因为引入了Data注解,那么我们需要
* 对它定义好的toString方法进行覆盖
*/
@Override
public String toString() {
return "Node{" +
"NodeId=" + NodeId +
", NodeName=" + NodeName +
'}';
}
}
3、二叉树类的设计
设计概念
-
既然了解到了节点的创建和组成,那么二叉树的创建和设计就显得比较简单了
-
二叉树需要什么?根节点嘛~
-
根节点从哪儿来?构造方法或者set传参嘛~
代码实现
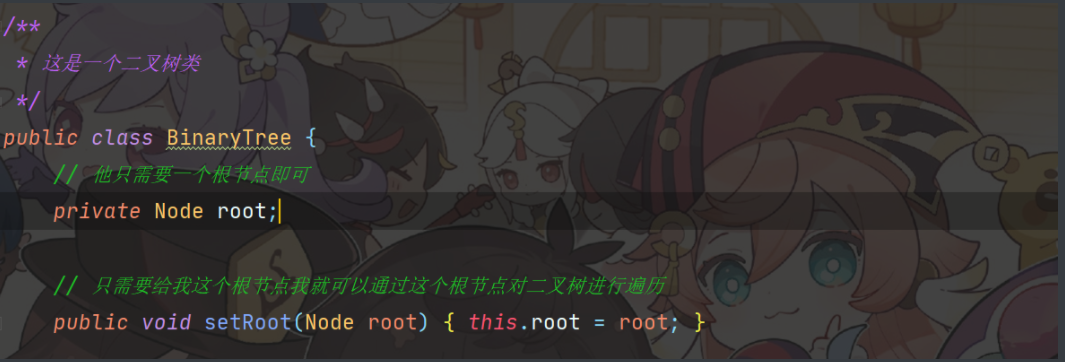
4、二叉树类的整体代码实现
/**
* 这是一个二叉树类
*/
public class BinaryTree {
// 他只需要一个根节点即可
private Node root;
// 只需要给我这个根节点我就可以通过这个根节点对二叉树进行遍历
public void setRoot(Node root) {
this.root = root;
}
// 前序遍历
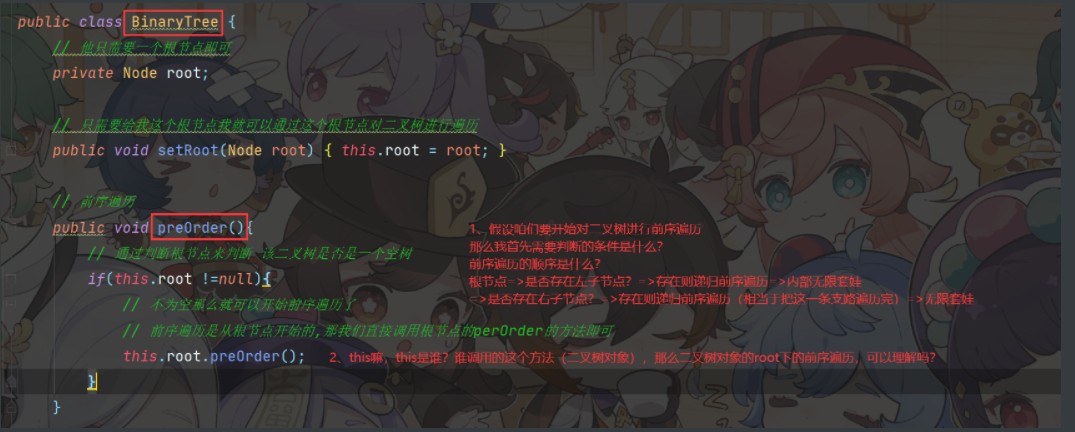
public void preOrder(){
// 通过判断根节点来判断 该二叉树是否是一个空树
if(this.root !=null){
// 不为空那么就可以开始前序遍历了
// 前序遍历是从根节点开始的,那我们直接调用根节点的perOrder的方法即可
this.root.preOrder();
}
}
// 中序遍历呢
public void infixOrder(){
// 左中右
// 根节点不为空
if(this.root!=null){
// 开始中序递归遍历
// this.root.getLeftNode().infixOrder();
/**
* 我算是明白了为什么,老师会说遍历遍历都是从父节点开始的
* 也就是根节点root,我这里犯的错误就是一个非常典型的例子
* 在我的例子当中,root的左子树下是没有子节点了
* 这个时候我从左子树开始,那么就会进行中序递归遍历
* 直接打印这个左子树的构造方法
* 然后因为该子树下没有子节点,所以下面哪条右子树的判断也不存在
* 所以最终最终,就只会打印左子树这一条记录
* 因为这个时候的根节点,是左子树,而非root
* 很妙啊
*/
this.root.infixOrder();
}
}
// 后序遍历
public void postOrder(){
// 根节点不为空
if(this.root!=null){
// 开始后序递归遍历
this.root.postOrder();
}
}
}
5、二叉树的前中后序遍历思路
我要着重说明一下,无论是前中后序遍历,起点永远都是从root根节点开始的,永远都是!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
概念
-
二叉树的遍历方式分为三种,前、中、后顺序遍历
-
前序遍历:顾名思义,先输出父节点(根节点)的内容,再遍历左子树和右子树
-
中序遍历:先遍历左子树的内容,再遍历父节点的内容,最后遍历右节点的内容
-
后序遍历:先遍历左右子树的内容,最后遍历父节点的内容
-
-
通过查看输出父节点内容的顺序,那么我们就可以确定该二叉树的遍历方式是前中后序的哪一种
代码实现思路

前序遍历--代码实现
莫得关系,这张图看起来生硬的话那我们来代码设计一下看看吧~
首先需要给咱们的节点类设置前序遍历的方法对吧,preOrder
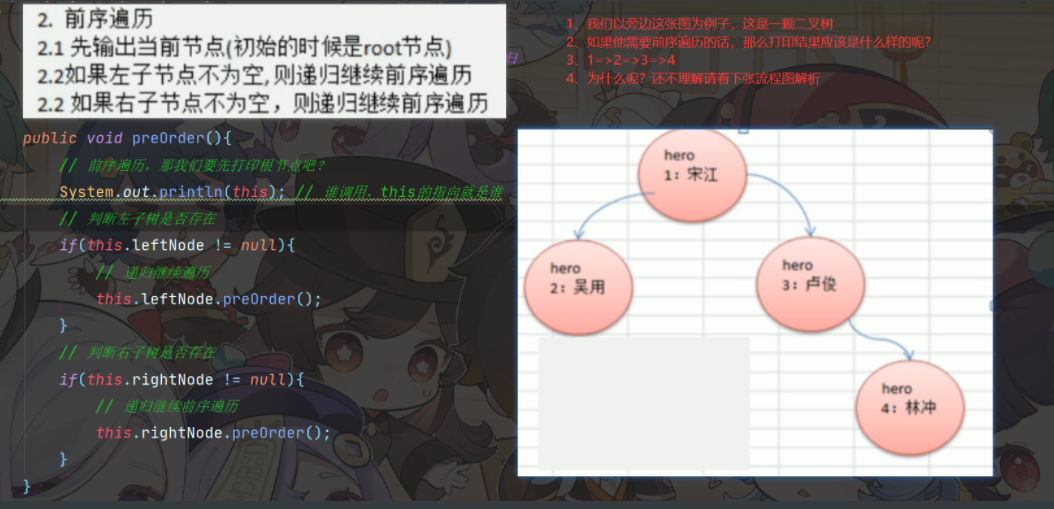
/**
* Node节点类的前序遍历方法
* 1、前序遍历首先肯定是从根节点开始的
* 2、判断当前左子树是否为空,不为空那么我们就对其进行前序遍历的递归
* 3、判断右子树是否为空,不为空那么我们就对其进行前序递归遍历
*/
public void preOrder(){
// 前序遍历,那我们要先打印根节点吧?
System.out.println(this); // 谁调用,this的指向就是谁
// 判断左子树是否存在
if(this.leftNode != null){
// 递归继续遍历
this.leftNode.preOrder();
}
// 判断右子树是否存在
if(this.rightNode != null){
// 递归继续前序遍历
this.rightNode.preOrder();
}
}那么二叉树需要这个方法吗?当然需要,方法肯定从二叉树哪里开始调用的啊
// 二叉树的前序遍历
public void preOrder(){
// 通过判断根节点来判断 该二叉树是否是一个空树
if(this.root !=null){
// 不为空那么就可以开始前序遍历了
// 前序遍历是从根节点开始的,那我们直接调用根节点的perOrder的方法即可
this.root.preOrder();
}
}前序遍历的运行过程
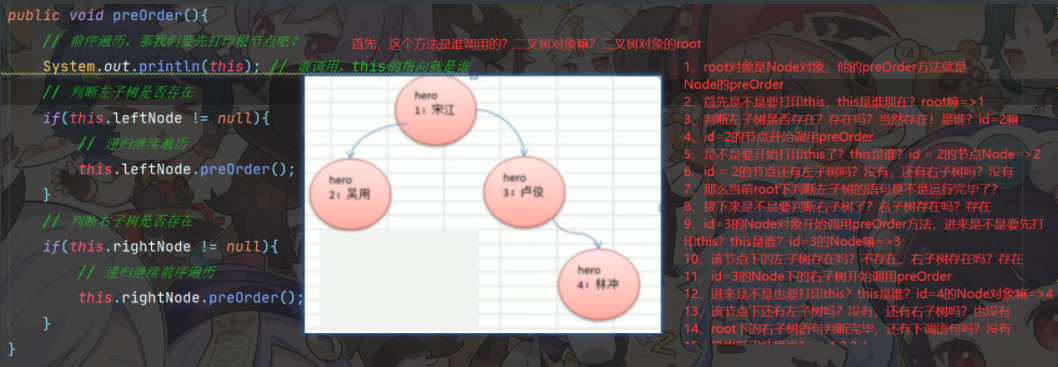
运行过程的文字解析,适合给没明白的小宝贝们理解使用
-
root对象是Node对象,他的preOrder方法就是Node的preOrder
-
首先是不是要打印this,this是谁现在?root嘛=>1
-
判断左子树是否存在?存在吗?当然存在!是谁? id=2嘛
-
id=2的节点开始调用preOrder
-
是不是要开始打印this了? this是谁? id=2的节点Node=>2
-
id = 2的节点还有左子树吗?没有,还有右子树吗?没有
-
-
那么当前root下判断左子树的语句是不是运行完毕了?
-
接下来是不是要判断右子树了?右子树存在吗?存在
-
id=3的Node对象开始调用preOrder方法,进来是不是要先打FDthis? this是谁? id=3的Node嘛=>3
-
该节点下的左子树存在吗?不有在,右子树存在吗?存在
-
id=3的Node下的右子树开始调用preOrder
-
进来是不是也要打印this? this是谁? id=4的Node对象嘛=>4
-
该节点下还有左子树吗?没有,还有右子树吗?也没有
-
-
-
root下的右子树语句判断完毕,还有下调语句吗?没有
中序遍历--代码实现
一样的,来设计方法,就相当于改下顺序,中序遍历的过程是什么样子的?

中序遍历的运行过程
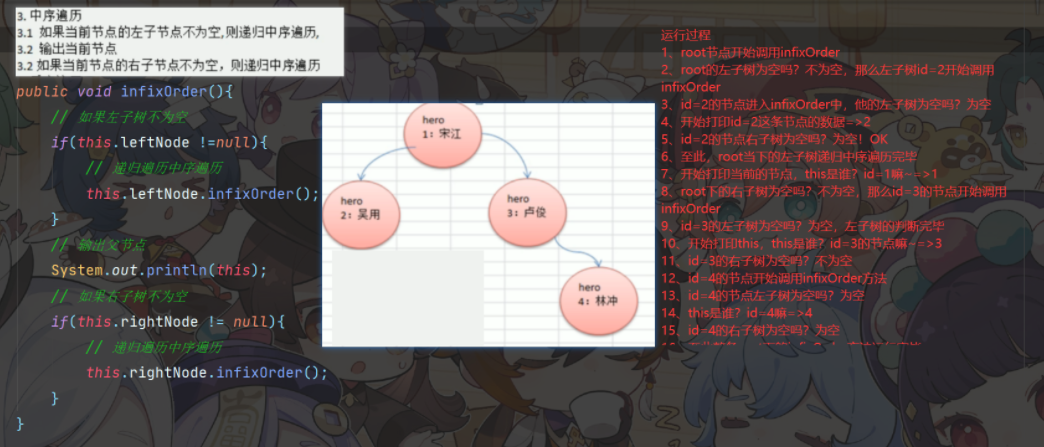
/**
* 中序遍历方法
* 1、先从左子树开始中序遍历,
* 2、输出父节点
* 3、最后从右子树中序遍历结束
*/
public void infixOrder(){
// 如果左子树不为空
if(this.leftNode !=null){
// 递归遍历中序遍历
this.leftNode.infixOrder();
}
// 输出父节点
System.out.println(this);
// 如果右子树不为空
if(this.rightNode != null){
// 递归遍历中序遍历
this.rightNode.infixOrder();
}
}// 中序遍历呢
public void infixOrder(){
// 左中右
// 根节点不为空
if(this.root!=null){
// 开始中序递归遍历
// this.root.getLeftNode().infixOrder();
/**
* 我算是明白了为什么,老师会说遍历遍历都是从父节点开始的
* 也就是根节点root,我这里犯的错误就是一个非常典型的例子
* 在我的例子当中,root的左子树下是没有子节点了
* 这个时候我从左子树开始,那么就会进行中序递归遍历
* 直接打印这个左子树的构造方法
* 然后因为该子树下没有子节点,所以下面哪条右子树的判断也不存在
* 所以最终最终,就只会打印左子树这一条记录
* 因为这个时候的根节点,是左子树,而非root
* 很妙啊
*/
this.root.infixOrder();
}
}文字描述部分
-
root节点开始调用infixOrder
-
root的左子树为空吗?不为空,那么左子树id=2开始调用infixOrder
-
id=2的节点进入infixOrder中,他的左子树为空吗?为空
-
开始打印id=2这条节点的数据=>2
-
id=2的节点右子树为空吗?为空! OK
-
-
至此,root当下的左子树递归中序遍历完毕
-
开始打印当前的节点,this是谁? id=1嘛~=>1
-
root下的右子树为空吗?不为空,那么id=3的节点开始调用infixOrder
-
id=3的左子树为空吗?为空,左子树的判断完毕
-
开始打Ethis,this是谁? id=3的节点嘛~=>3
-
id=3的右子树为空吗?不为空
-
id=4的节点开始调用infixOrder方法
-
id=4的节点左子树为空吗?为空
-
this是谁? id=4嘛=>4
-
id-4的右子树为空吗?为空
-
-
-
至此,root下的全部语句运行完毕
后续遍历--代码实现
还是一样的味道~,不过后续遍历要注意哦,跟之前的感觉有点不一样

图文描述
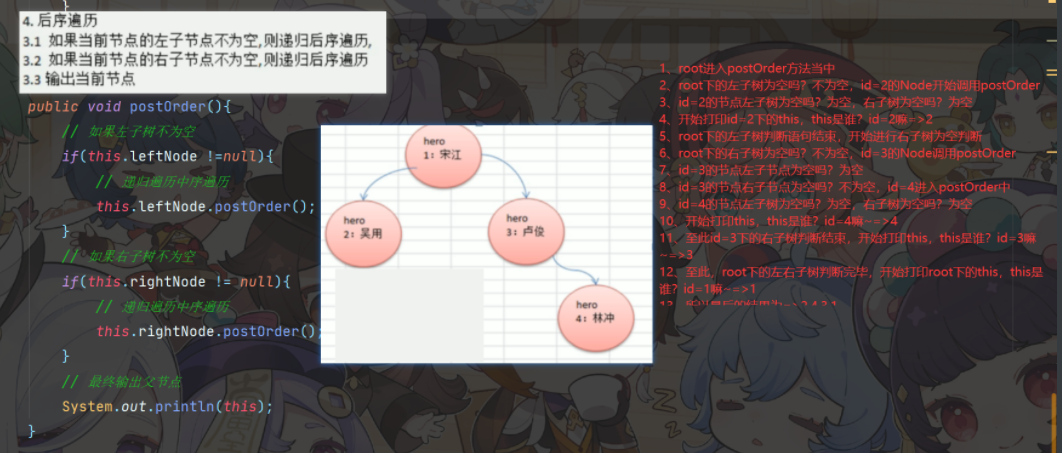
Node下的postOrder
// 后序遍历
public void postOrder(){
// 如果左子树不为空
if(this.leftNode !=null){
// 递归遍历中序遍历
this.leftNode.postOrder();
}
// 如果右子树不为空
if(this.rightNode != null){
// 递归遍历中序遍历
this.rightNode.postOrder();
}
// 最终输出父节点
System.out.println(this);
}二叉树下的postOrder
// 后序遍历
public void postOrder(){
// 根节点不为空
if(this.root!=null){
// 开始后序递归遍历
this.root.postOrder();
}
}文字描述
-
root进入postOrder方法当中
-
root下的左子树为空吗?不为空,id=2的Node开始调用postOrder
-
id=2的节点左子树为空吗?为空,右子树为空吗?为空
-
开始打印id=2下的this,this是谁? id=2嘛=>2
-
-
root下的左子树判断语句结束,开始进行右子树为空判断
-
root下的右子树为空吗?不为空,id=3的Node调用postOrder
-
id=3的节点左子节点为空吗?为空
-
id=3的节点右子节点为空吗?不为空,id=4进入postOrder中
-
id=4的节点左子树为空吗?为空,右子树为空吗?为空
-
开始打印this,this是谁? id=-4嘛~=>4
-
-
至此id=3下的右子树判断结束,开始打印this,this是谁? id=3嘛~=>3
-
-
至此,root下的左右子树判晰完毕,开始打印root下的this,this是谁?id=1嘛~=>1
1.3、设计方法开始测试
假如这里有一颗二叉树,他的结构是这样的
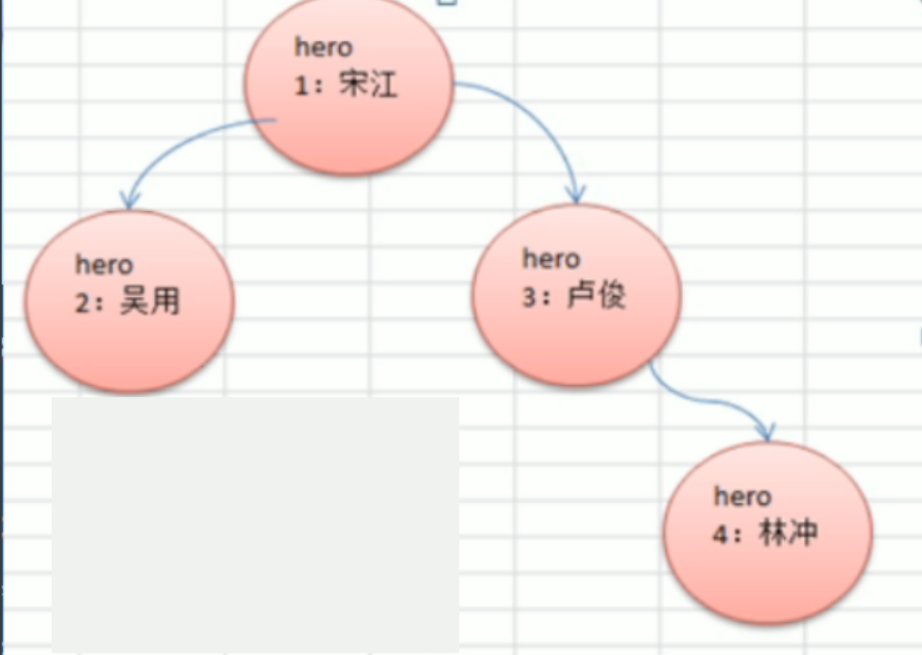
-
那么我们首先应该怎么做?
-
先创建一颗二叉树对吧?
-
然后开始创建我们的节点,因为现在是起步节点,先不忙使用递归的方式创建二叉树
-
那么节点创建完毕,我们是不是要开始编织节点的关系?
-
编织完关系过后,我们是不是需要给二叉树的对象设置根节点--root?
-
开始调用前中后序遍历
接下来的测试方法我使用的是Maven的Junit的测试类
1、前置方法的设置--@Before
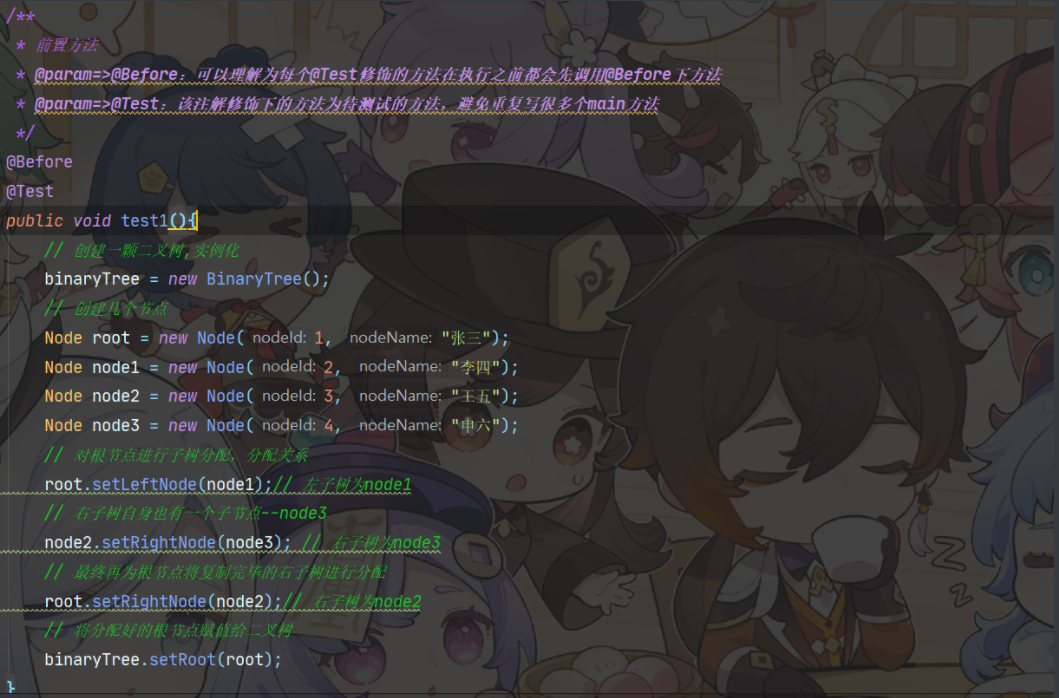
/**
* 前置方法
* @param=>@Before:可以理解为每个@Test修饰的方法在执行之前都会先调用@Before下方法
* @param=>@Test:该注解修饰下的方法为待测试的方法,避免重复写很多个main方法
*/
@Before
@Test
public void test1(){
// 创建一颗二叉树,实例化
binaryTree = new BinaryTree();
// 创建几个节点
Node root = new Node(1, "张三");
Node node1 = new Node(2, "李四");
Node node2 = new Node(3, "王五");
Node node3 = new Node(4, "申六");
// 对根节点进行子树分配,分配关系
root.setLeftNode(node1);// 左子树为node1
// 右子树自身也有一个子节点--node3
node2.setRightNode(node3); // 右子树为node3
// 最终再为根节点将复制完毕的右子树进行分配
root.setRightNode(node2);// 右子树为node2
// 将分配好的根节点赋值给二叉树
binaryTree.setRoot(root);
}2、前序遍历
来吧,开始调用前序遍历
/**
* 前序遍历
*/
@Test
public void preOrder(){
// 开始前序遍历,结果肯定是1234
binaryTree.preOrder();
}结果为
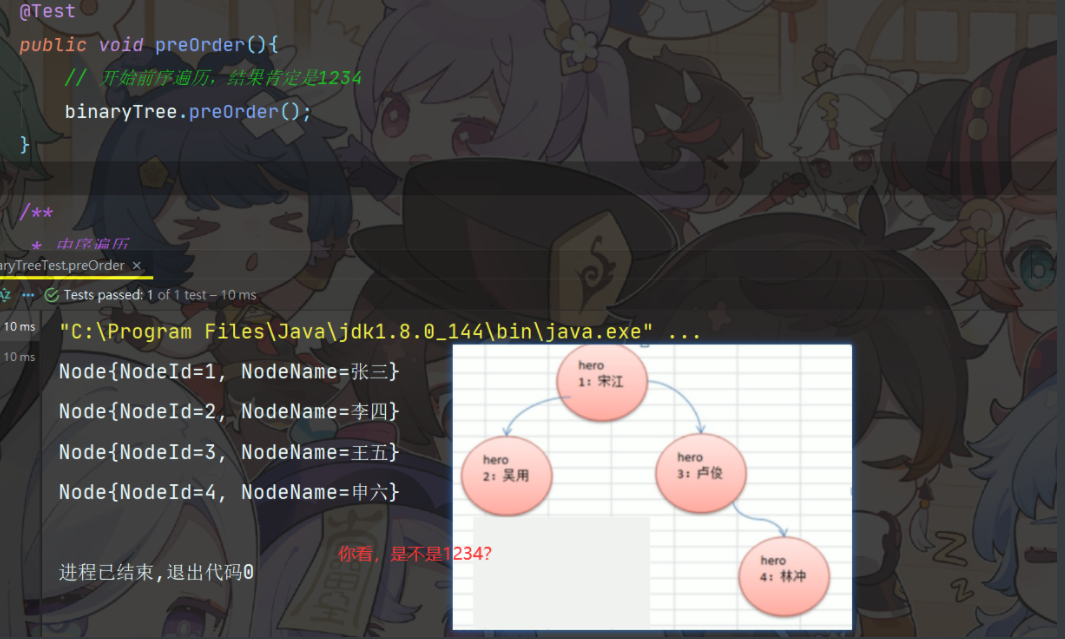
3、中序遍历
/**
* 中序遍历
*/
@Test
public void infixOrder(){
System.out.println("中序遍历开始");
// 中序遍历--2134
binaryTree.infixOrder();
}结果为
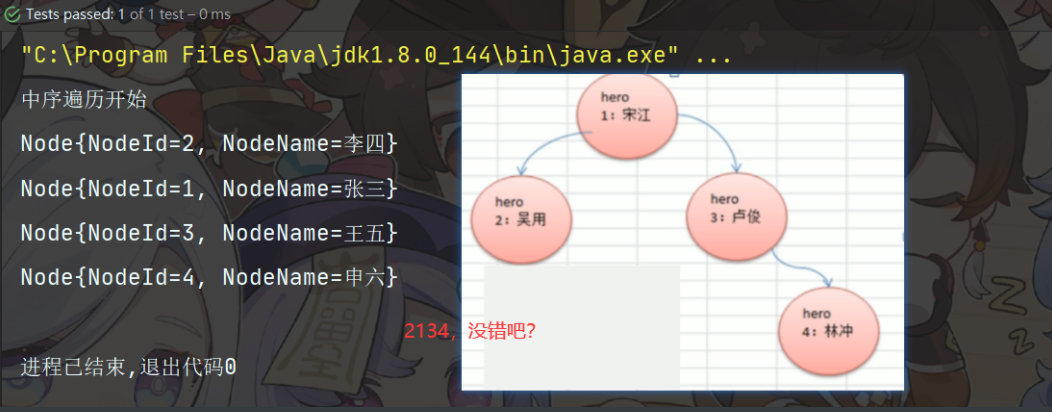
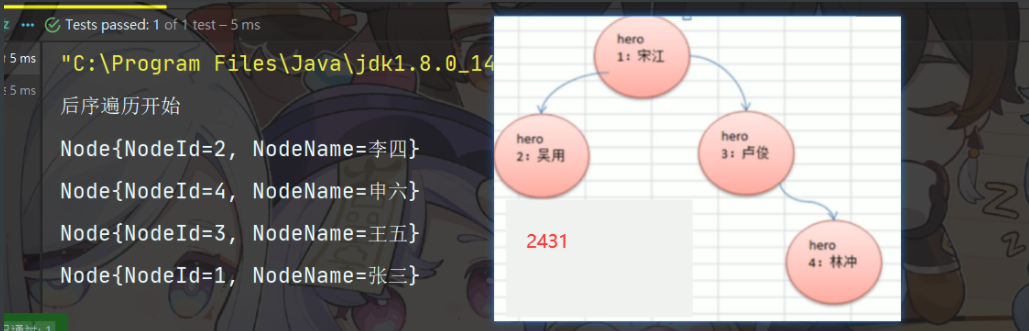
4、后序遍历
代码设计


 浙公网安备 33010602011771号
浙公网安备 33010602011771号