图形学（2）MVP变换

Model View transformation（模型视图变换）

注意到定义一个相机我们需要三个矢量：

• 位置 \(\vec{e}\)
• 视线方向 \(\hat{g}\)
• 向上方向 \(\hat{t}\)
  

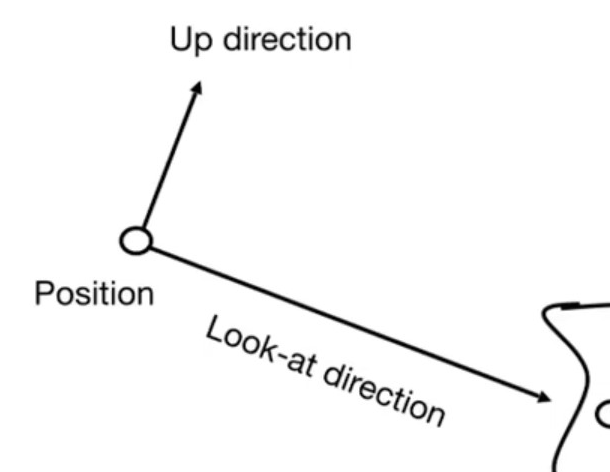
注意到我们的目标就是将相机固定到原点，并使 \(\hat{g},\hat{t}\) 和坐标轴对齐。

约定

我们最终让相机的向上方向 \(\hat{t}\) 为 \(y\) 轴，视线方向 \(\hat{g}\) 为 \(-z\) 轴。

移动 \(\vec{e}\) 至原点

\[T_{view}=\begin{bmatrix} 1 & 0 & 0 & -x_e\\ 0 & 1 & 0 & -y_e\\ 0 & 0 & 1 & -z_e\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

将 \(\hat{g},\hat{t}\) 与坐标轴对齐

考虑其逆矩阵：

\[R^{-1}_{view}=\begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_{\hat{t}} & x_{-\hat{g}} & 0\\ y_{\hat{g}\times\hat{t}} & y_{\hat{t}} & y_{-\hat{g}} & 0\\ z_{\hat{g}\times\hat{t}} & z_{\hat{t}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

注意到 这是一个正交矩阵，其逆矩阵为其转置，故有：

\[R_{view}=(R^{-1}_{view})^\mathbf{T}= \begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0\\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0\\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

则有 \(M_{view}=R_{view}T_{view}\)；让所有物体和相机一起做同样的变换，即得到结果。

Projection Transformation（投影变换）

Orthographic Projection（正交投影）

将长方体 \([l,r]\times[b,t]\times[f,n]\) 变换到 \([-1,1]^3\)（正规立方体），注意 \(f\le n\)，因为我们看向 \(-z\) 方向。

\[M_{ortho}=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t - b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

Perspective Projection（透视投影）

我们先将透视投影转到正交投影，然后进行一个正交投影得到正规立方体。
考虑一个近平面 \(z=n\)，一个远平面 \(z=f\)，对任意一条从原点出发穿过两个平面的射线，交近平面于 \(A\)，交远平面于 \(B\)，我们希望映射保证 \(A\rightarrow A,B\rightarrow C\)，其中 \(C\) 满足 \(x_C=x_A,y_C=y_A,z_C=f\)，即 \(A\) 在远平面上的投影。
简单计算有：

\[M_{persp}=\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix} \]

Viewport Transformation（视口变换）

\([-1,1]^3\rightarrow[0,width]\times[0,height]\times[-1,1]\) 即可。

\[M_{viewport}= \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}\\ 0 & \frac{height}{2} & 0 & \frac{height}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

参数的计算

上文矩阵中的 \(l,r,b,t,f,n\) 决定了可视区域，其中 \(l,r,b,t\) 根据 FOV，长宽比（aspect_ratio）和 \(f,n\) 计算，这里使用 fovY：

\[\tan\frac{fovY}{2}=\frac{t}{\left|n\right|}\\ aspect\ ratio=\frac{r}{t} \]