import numpy as np
import matplotlib.pyplot as plt
"""
凹函数:斜率递减(收益递减效应) 柯布-道格拉斯模型(Cobb-Douglass model)是经济学中使用最广泛的模型之一
给定L个工人和K个单位资本,总产出如下所示:
资本以机器数量作为衡量,机器数量=原有机器数量+投资-折旧
产出 = 常数 * (L ** a) * (K ** (1-a)) 其中a是介于0到1之间的实数,表示劳动力的相对重要性
完整的简单增长模型由4个方程组成 (O=产出,M=机器,I=投资,C=消费,s=储蓄率,d=折旧率)
1.产出函数:O(t) = 常数 * (L ** a) * (K ** (1-a))
2.投资规则:I(t) = s * O(t)
3.消费-投资方程:O(t) = C(t) + I(t) 产出一部分用于消费,一部分用于再投资
4.投资-折旧方程:M(t+1) = M(t) + I(t) - d*M(t)
"""
a, L, M, I, s, d, n = 0.5, 10000, 100, 200, 0.2, 0.1, 100
# 第一年的产出,假设常数为1
K = M
O1 = (L ** a) * (K ** (1-a))
I = s * O1
M = K - d * M
# 第二年的产出
K = M + I
O2 = (L ** a) * (K ** (1-a))
I = s * O2
M = K - d * K
# 第三年的产出
K = M + I
O3 = (L ** a) * (K ** (1-a))
def economic_growth_model(a, L, M, I, s, d, n):
K = M
Time = [t for t in range(n)]
Output = []
for i in range(n):
O = (L ** a) * (K ** (1-a))
Output.append(O)
I = s * O
M = K - d * K
K = M + I
return Time, Output
a, L, M, I, s, d, n = 0.5, 10000, 100, 200, 0.2, 0.1, 100
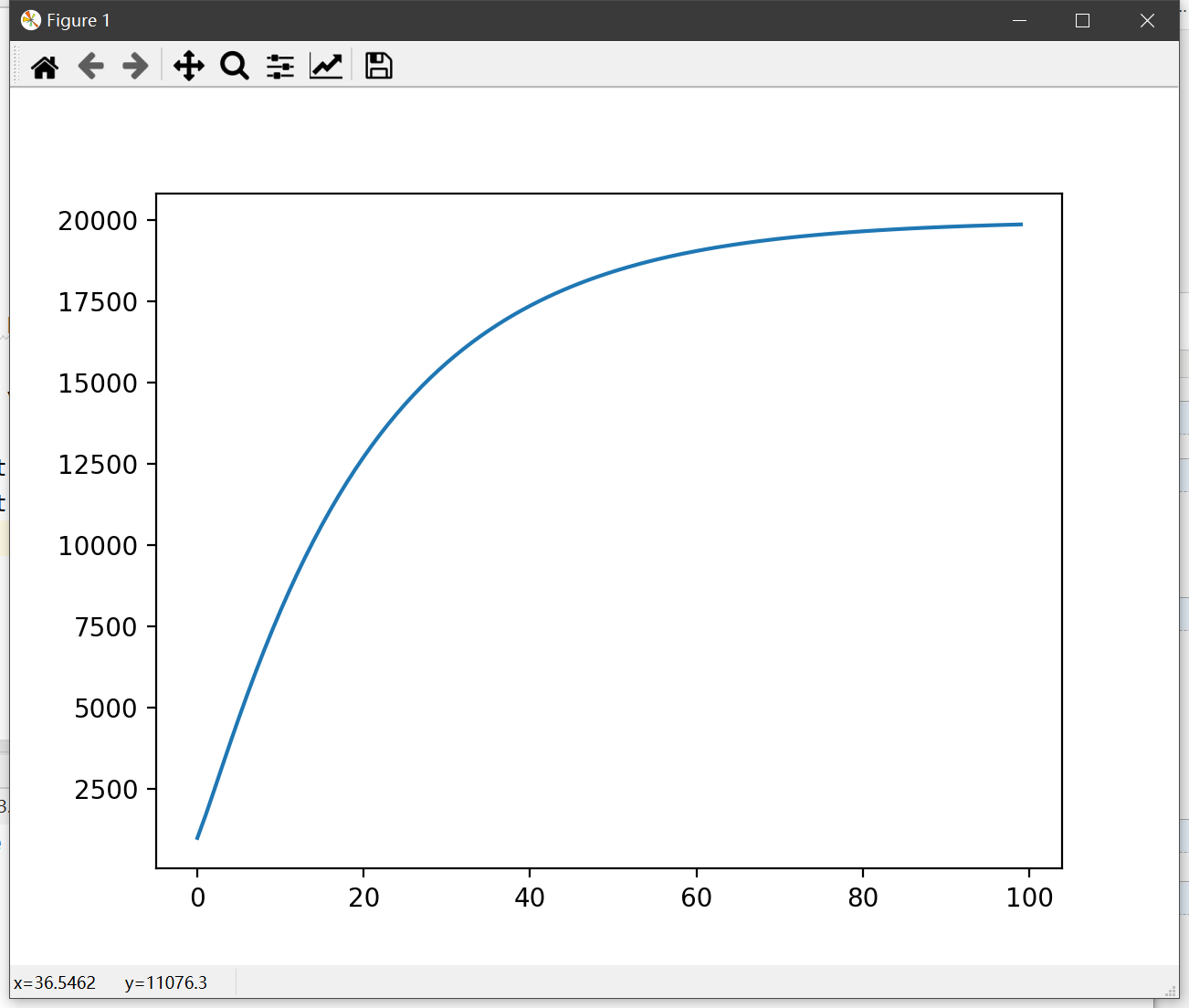
x, y = economic_growth_model(a, L, M, I, s, d, n)
plt.plot(x, y)
plt.show()
![]()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号