回溯算法

回溯算法

背景

电话号码的字母组合：

暴力循环枚举：

for(i in "abc")
	for(j in "def")
		组合；

可以得到有3*3=9种。

问题：如果构成的字符串长度为3或长度为一个参数n呢？
可以看出，单纯的循环”表达能力有限“，再举一个简单例子：
{1，2，3，4}两两组合有多少种组合？
（1，2）、（1，3）、（1，4）、（2，3）、（2，4）、（3，4）
同样地，用嵌套循环去搜索：

for(i=0;i<nums.length - 1;i++)
	for(j=i+1;j<nums.length;j++)
		组合；

思考如果不是两两组合，而是k个数组合呢？此时嵌套 k 层循环应该怎么表达？
引入：递归中的回溯算法：当前操作；递归；撤回当前操作，这就是回溯的过程。
例如：(1,?) => (1,2) => (1,?) 这个过程就是回溯，最后一步就是回溯操作。

一些思考：其实for循环中也存在回溯，只是循环没有回退的过程，只能穷举明确有多少层的循环，而回溯有具体的回退操作，且常常伴随递归，可以扩展到k（k为参数）层。
回溯有一个增量构造答案的过程。
递归中回溯的实现我们应该抓大放小，主要关注边界条件与非边界条件。

回溯的类型：

1. 子集型回溯：电话号码的字母组合、子集、分割回文串
2. 组合型：组合、组合的总和、括号生成
3. 排列型：全排列、n皇后

回溯三问：

从答案的视角：
背景电话号码字母组合问题：
用一个path数组记录路径上的字母

1. 当前操作：枚举path[i]要填入的字母
2. 子问题：构造字符串>=i的部分
3. 下一个子问题：狗仔字符串>=i+1的部分

树与回溯

{1，2，3，4} 两两组合

1. 从答案视角：枚举第i个答案选哪个元素

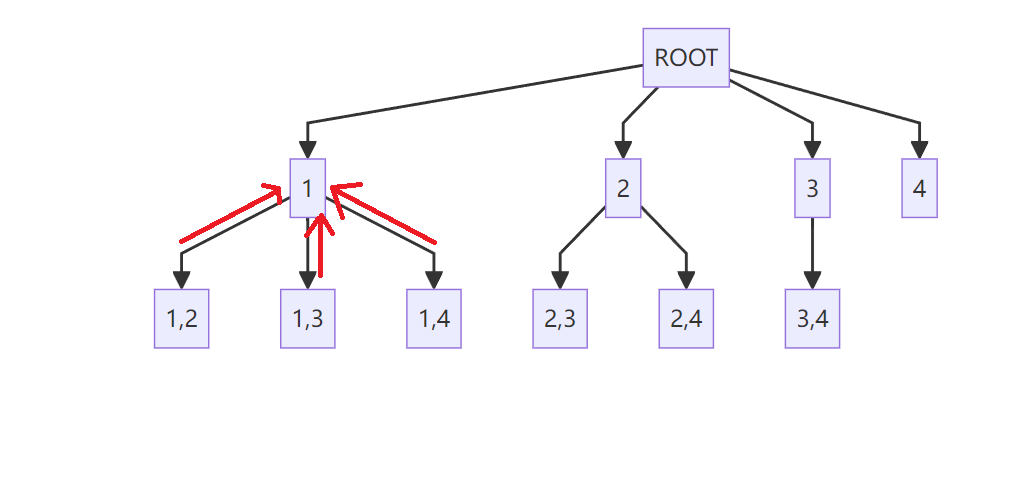
往回走即为回溯的过程，在dfs中，如果还有for循环，在循环里递归i还是j，画递归搜索树来理解

三类问题层层递进

集合{1，2，3}

1. 子集型：求集合子集

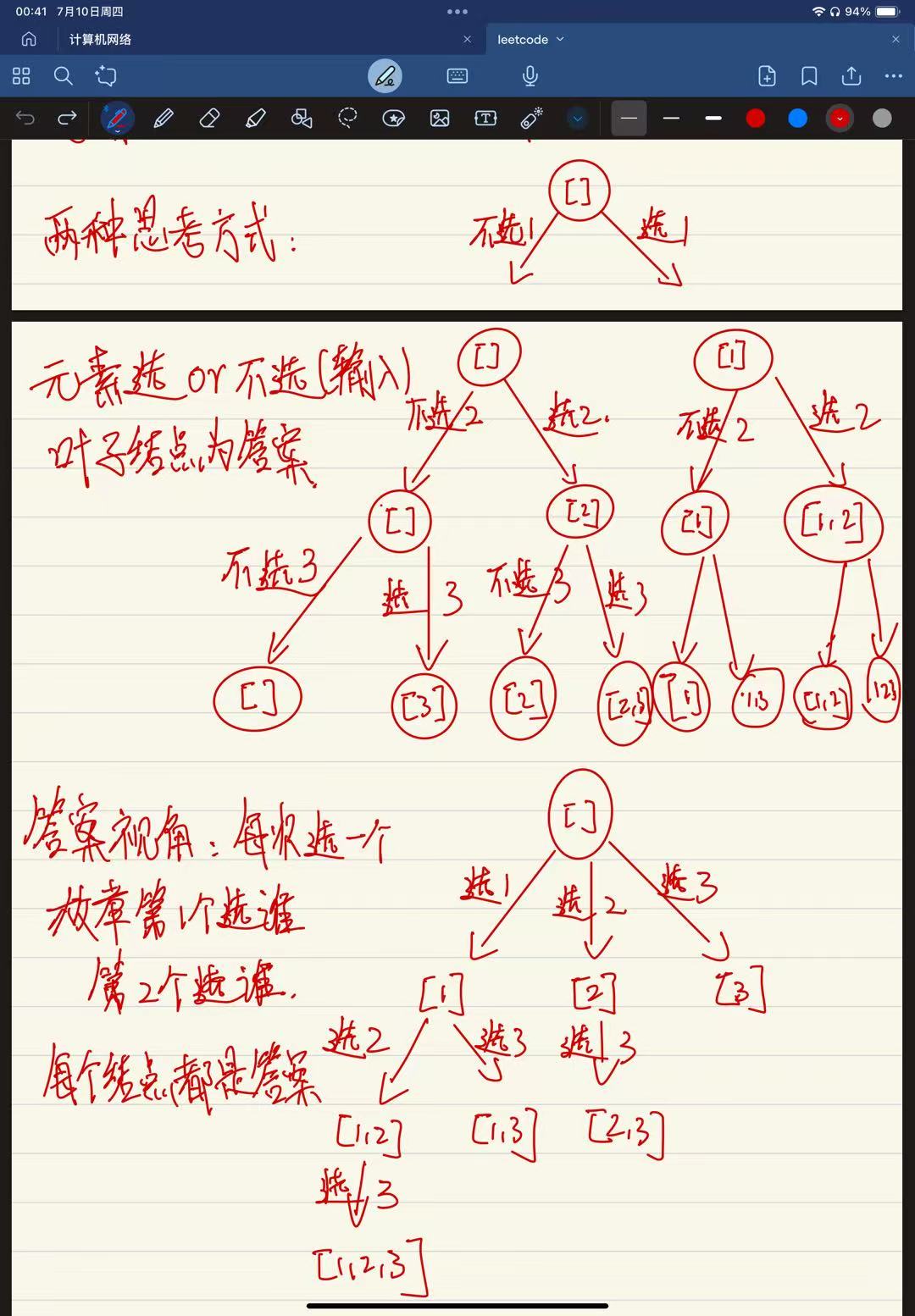
为什么是DFS?因为我们递归回溯是一条路走到黑，通过回溯（递归中的回退与撤回当前操作）操作返回到上一节点。

2. 组合型：求集合中k个数的组合（k<n）

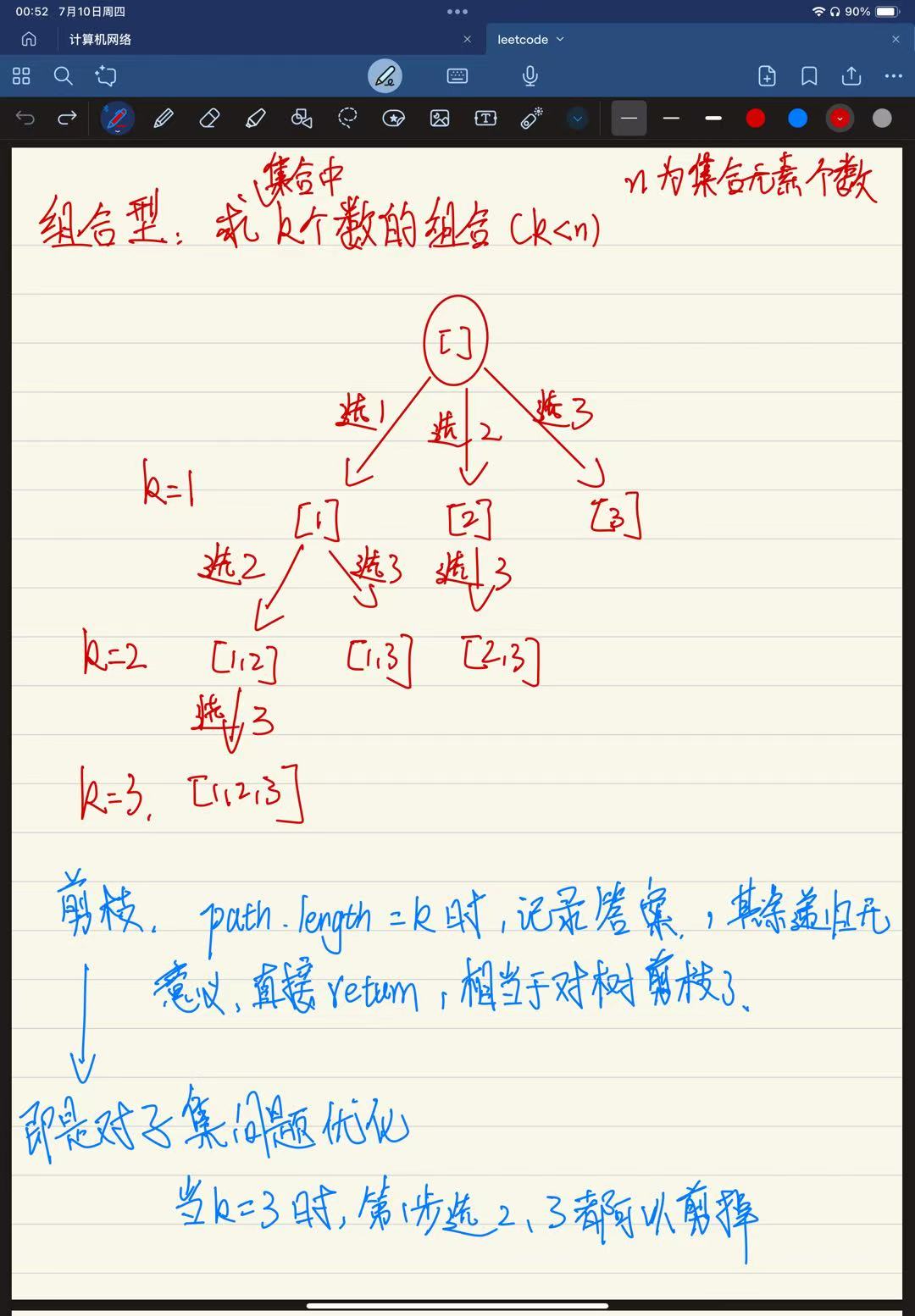
3. 排列型：求集合的全排列

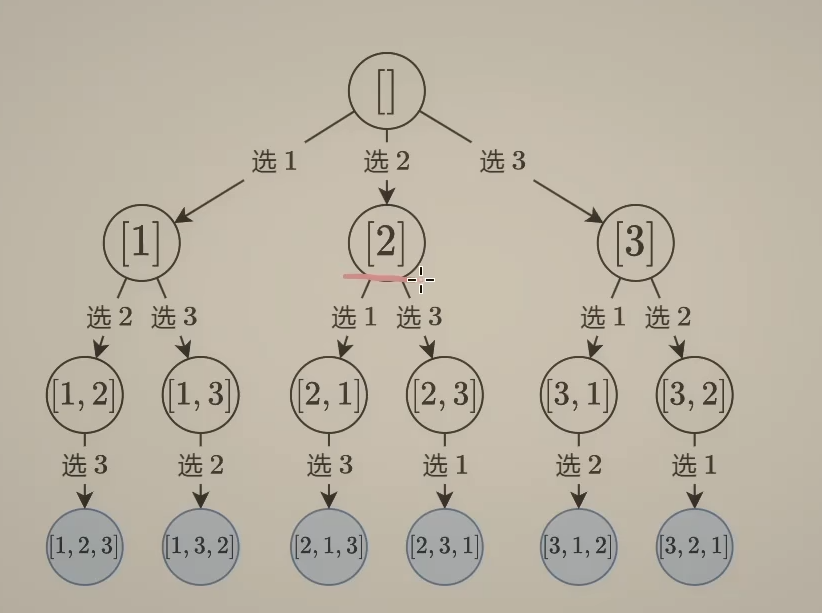
其他型在第一步选了2后通常就不能选1了，避免产生重复结果（顺序不重要），在全排序中顺序不同也表示不同集合，所以回退后能选择的元素除了在本树中已经选的元素外，其他都可以选。

回溯伪代码模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径, 选择列表); // 递归
        回溯，撤销处理结果;
    }
}